Physics Exam > Physics Questions > Consider the case of a 3 dimensional harmonic...
Start Learning for Free
Consider the case of a 3 dimensional harmonic oscillator. Choose the correct statement.
- a)In case of an anisotropic oscillator, there is no degeneracy since the potential is not symmetric
- b)Both isotropic and anisotropic oscillators have zero point energy
- c)In case of an isotropic harmonic oscillator, the energy levels can be degenerate
- d)Isotropic oscillators have zero kinetic energy in the ground state
Correct answer is option 'A,B,C'. Can you explain this answer?
| FREE This question is part of | Download PDF Attempt this Test |
Verified Answer
Consider the case of a 3 dimensional harmonic oscillator. Choose the c...
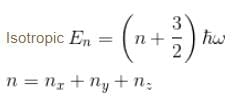
can be degenerate
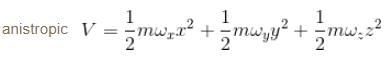
No symmetry in potential. Energy levels cannot be degenerate. Both have zero point energy.
The correct answers are: In case of an isotropic harmonic oscillator, the energy levels can be degenerate, In case of an anisotropic oscillator, there is no degeneracy since the potential is not symmetric, Both isotropic and anisotropic oscillators have zero point energy
Most Upvoted Answer
Consider the case of a 3 dimensional harmonic oscillator. Choose the c...
Introduction:
The 3-dimensional harmonic oscillator is a system in which a particle is subjected to a potential energy that varies quadratically with its displacement from the equilibrium position in all three dimensions. This system has several important properties, including degeneracy and zero-point energy. In this response, we will analyze each statement and explain why options A, B, and C are correct.
Statement A: In case of an anisotropic oscillator, there is no degeneracy since the potential is not symmetric.
An anisotropic oscillator is one in which the potential energy is different in different directions. This means that the oscillator is not symmetric, and thus, it does not possess any degeneracy. Degeneracy refers to the situation where multiple energy levels have the same energy. In an anisotropic oscillator, the potential energy along different axes is different, resulting in different energy levels for different directions. Therefore, there is no degeneracy in an anisotropic oscillator.
Statement B: Both isotropic and anisotropic oscillators have zero-point energy.
The zero-point energy is the minimum energy that a system can possess even at its ground state (lowest energy level). Both isotropic and anisotropic oscillators have zero-point energy. This is because the zero-point energy arises from the Heisenberg uncertainty principle, which states that the position and momentum of a particle cannot be simultaneously known with absolute certainty. As a result, even in the ground state, the particle still possesses some energy due to the uncertainty in its position and momentum. This energy is known as the zero-point energy, and it exists in both isotropic and anisotropic oscillators.
Statement C: In case of an isotropic harmonic oscillator, the energy levels can be degenerate.
An isotropic harmonic oscillator is one in which the potential energy is the same in all directions. This means that the oscillator is symmetric, and it possesses degeneracy. In an isotropic oscillator, the potential energy is solely determined by the distance from the equilibrium position and not by the direction. This results in the same energy levels for different directions, leading to degeneracy. Therefore, energy levels in an isotropic harmonic oscillator can be degenerate.
Conclusion:
In summary, the statements A, B, and C are all correct. In an anisotropic oscillator, there is no degeneracy due to the lack of symmetry in the potential energy. Both isotropic and anisotropic oscillators have zero-point energy arising from the Heisenberg uncertainty principle. In an isotropic harmonic oscillator, the energy levels can be degenerate due to the symmetry of the potential energy.
The 3-dimensional harmonic oscillator is a system in which a particle is subjected to a potential energy that varies quadratically with its displacement from the equilibrium position in all three dimensions. This system has several important properties, including degeneracy and zero-point energy. In this response, we will analyze each statement and explain why options A, B, and C are correct.
Statement A: In case of an anisotropic oscillator, there is no degeneracy since the potential is not symmetric.
An anisotropic oscillator is one in which the potential energy is different in different directions. This means that the oscillator is not symmetric, and thus, it does not possess any degeneracy. Degeneracy refers to the situation where multiple energy levels have the same energy. In an anisotropic oscillator, the potential energy along different axes is different, resulting in different energy levels for different directions. Therefore, there is no degeneracy in an anisotropic oscillator.
Statement B: Both isotropic and anisotropic oscillators have zero-point energy.
The zero-point energy is the minimum energy that a system can possess even at its ground state (lowest energy level). Both isotropic and anisotropic oscillators have zero-point energy. This is because the zero-point energy arises from the Heisenberg uncertainty principle, which states that the position and momentum of a particle cannot be simultaneously known with absolute certainty. As a result, even in the ground state, the particle still possesses some energy due to the uncertainty in its position and momentum. This energy is known as the zero-point energy, and it exists in both isotropic and anisotropic oscillators.
Statement C: In case of an isotropic harmonic oscillator, the energy levels can be degenerate.
An isotropic harmonic oscillator is one in which the potential energy is the same in all directions. This means that the oscillator is symmetric, and it possesses degeneracy. In an isotropic oscillator, the potential energy is solely determined by the distance from the equilibrium position and not by the direction. This results in the same energy levels for different directions, leading to degeneracy. Therefore, energy levels in an isotropic harmonic oscillator can be degenerate.
Conclusion:
In summary, the statements A, B, and C are all correct. In an anisotropic oscillator, there is no degeneracy due to the lack of symmetry in the potential energy. Both isotropic and anisotropic oscillators have zero-point energy arising from the Heisenberg uncertainty principle. In an isotropic harmonic oscillator, the energy levels can be degenerate due to the symmetry of the potential energy.
Free Test
FREE
| Start Free Test |
Community Answer
Consider the case of a 3 dimensional harmonic oscillator. Choose the c...
D

|
Explore Courses for Physics exam
|

|
Similar Physics Doubts
Consider the case of a 3 dimensional harmonic oscillator. Choose the correct statement.a)In case of an anisotropic oscillator, there is no degeneracy since the potential is not symmetricb)Both isotropic and anisotropic oscillators have zero point energyc)In case of an isotropic harmonic oscillator, the energy levels can be degenerated)Isotropic oscillators have zero kinetic energy in the ground stateCorrect answer is option 'A,B,C'. Can you explain this answer?
Question Description
Consider the case of a 3 dimensional harmonic oscillator. Choose the correct statement.a)In case of an anisotropic oscillator, there is no degeneracy since the potential is not symmetricb)Both isotropic and anisotropic oscillators have zero point energyc)In case of an isotropic harmonic oscillator, the energy levels can be degenerated)Isotropic oscillators have zero kinetic energy in the ground stateCorrect answer is option 'A,B,C'. Can you explain this answer? for Physics 2024 is part of Physics preparation. The Question and answers have been prepared according to the Physics exam syllabus. Information about Consider the case of a 3 dimensional harmonic oscillator. Choose the correct statement.a)In case of an anisotropic oscillator, there is no degeneracy since the potential is not symmetricb)Both isotropic and anisotropic oscillators have zero point energyc)In case of an isotropic harmonic oscillator, the energy levels can be degenerated)Isotropic oscillators have zero kinetic energy in the ground stateCorrect answer is option 'A,B,C'. Can you explain this answer? covers all topics & solutions for Physics 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for Consider the case of a 3 dimensional harmonic oscillator. Choose the correct statement.a)In case of an anisotropic oscillator, there is no degeneracy since the potential is not symmetricb)Both isotropic and anisotropic oscillators have zero point energyc)In case of an isotropic harmonic oscillator, the energy levels can be degenerated)Isotropic oscillators have zero kinetic energy in the ground stateCorrect answer is option 'A,B,C'. Can you explain this answer?.
Consider the case of a 3 dimensional harmonic oscillator. Choose the correct statement.a)In case of an anisotropic oscillator, there is no degeneracy since the potential is not symmetricb)Both isotropic and anisotropic oscillators have zero point energyc)In case of an isotropic harmonic oscillator, the energy levels can be degenerated)Isotropic oscillators have zero kinetic energy in the ground stateCorrect answer is option 'A,B,C'. Can you explain this answer? for Physics 2024 is part of Physics preparation. The Question and answers have been prepared according to the Physics exam syllabus. Information about Consider the case of a 3 dimensional harmonic oscillator. Choose the correct statement.a)In case of an anisotropic oscillator, there is no degeneracy since the potential is not symmetricb)Both isotropic and anisotropic oscillators have zero point energyc)In case of an isotropic harmonic oscillator, the energy levels can be degenerated)Isotropic oscillators have zero kinetic energy in the ground stateCorrect answer is option 'A,B,C'. Can you explain this answer? covers all topics & solutions for Physics 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for Consider the case of a 3 dimensional harmonic oscillator. Choose the correct statement.a)In case of an anisotropic oscillator, there is no degeneracy since the potential is not symmetricb)Both isotropic and anisotropic oscillators have zero point energyc)In case of an isotropic harmonic oscillator, the energy levels can be degenerated)Isotropic oscillators have zero kinetic energy in the ground stateCorrect answer is option 'A,B,C'. Can you explain this answer?.
Solutions for Consider the case of a 3 dimensional harmonic oscillator. Choose the correct statement.a)In case of an anisotropic oscillator, there is no degeneracy since the potential is not symmetricb)Both isotropic and anisotropic oscillators have zero point energyc)In case of an isotropic harmonic oscillator, the energy levels can be degenerated)Isotropic oscillators have zero kinetic energy in the ground stateCorrect answer is option 'A,B,C'. Can you explain this answer? in English & in Hindi are available as part of our courses for Physics.
Download more important topics, notes, lectures and mock test series for Physics Exam by signing up for free.
Here you can find the meaning of Consider the case of a 3 dimensional harmonic oscillator. Choose the correct statement.a)In case of an anisotropic oscillator, there is no degeneracy since the potential is not symmetricb)Both isotropic and anisotropic oscillators have zero point energyc)In case of an isotropic harmonic oscillator, the energy levels can be degenerated)Isotropic oscillators have zero kinetic energy in the ground stateCorrect answer is option 'A,B,C'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
Consider the case of a 3 dimensional harmonic oscillator. Choose the correct statement.a)In case of an anisotropic oscillator, there is no degeneracy since the potential is not symmetricb)Both isotropic and anisotropic oscillators have zero point energyc)In case of an isotropic harmonic oscillator, the energy levels can be degenerated)Isotropic oscillators have zero kinetic energy in the ground stateCorrect answer is option 'A,B,C'. Can you explain this answer?, a detailed solution for Consider the case of a 3 dimensional harmonic oscillator. Choose the correct statement.a)In case of an anisotropic oscillator, there is no degeneracy since the potential is not symmetricb)Both isotropic and anisotropic oscillators have zero point energyc)In case of an isotropic harmonic oscillator, the energy levels can be degenerated)Isotropic oscillators have zero kinetic energy in the ground stateCorrect answer is option 'A,B,C'. Can you explain this answer? has been provided alongside types of Consider the case of a 3 dimensional harmonic oscillator. Choose the correct statement.a)In case of an anisotropic oscillator, there is no degeneracy since the potential is not symmetricb)Both isotropic and anisotropic oscillators have zero point energyc)In case of an isotropic harmonic oscillator, the energy levels can be degenerated)Isotropic oscillators have zero kinetic energy in the ground stateCorrect answer is option 'A,B,C'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice Consider the case of a 3 dimensional harmonic oscillator. Choose the correct statement.a)In case of an anisotropic oscillator, there is no degeneracy since the potential is not symmetricb)Both isotropic and anisotropic oscillators have zero point energyc)In case of an isotropic harmonic oscillator, the energy levels can be degenerated)Isotropic oscillators have zero kinetic energy in the ground stateCorrect answer is option 'A,B,C'. Can you explain this answer? tests, examples and also practice Physics tests.

|
Explore Courses for Physics exam
|

|
Suggested Free Tests
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.


















