JEE Exam > JEE Questions > The mean lives of a radioactive substance are...
Start Learning for Free
The mean lives of a radioactive substance are 1620 years and 405 years for α - emission and β - emission respectively. Find the time during which three-fourth of a sample will decay if it is decaying both by α – emission and β – emission simultaneously.
- a)449 years
- b)450 years
- c)365 years
- d)439 years
Correct answer is option 'A'. Can you explain this answer?
Verified Answer
The mean lives of a radioactive substance are 1620 years and 405 years...
The decay constant λ is the reciprocal of the mean life τ
Thus,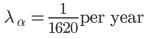
and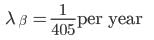
∴ Total decay constant, λ = λα + λβ
or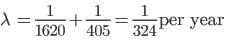
We know that
N = N0e–λt
When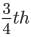
part of the sample has disintegrated, N = N0/4
∴
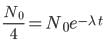
or eλt = 4
Taking logarithm of both sides, we get
or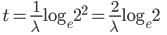
= 2×324 × 0.693 = 449 year
Thus,
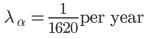
and
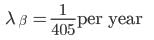
∴ Total decay constant, λ = λα + λβ
or
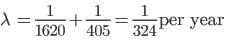
We know that
N = N0e–λt
When
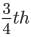part of the sample has disintegrated, N = N0/4∴
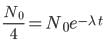
or eλt = 4
Taking logarithm of both sides, we get
or
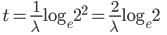
= 2×324 × 0.693 = 449 year
Most Upvoted Answer
The mean lives of a radioactive substance are 1620 years and 405 years...
Two different isotopes. This means that if we were to take a large number of atoms of each isotope and observe their decay, the average time it would take for half of the atoms to decay (also known as the half-life) would be 1620 years for one isotope and 405 years for the other.
For example, if we start with 1000 atoms of the 1620-year isotope, after 1620 years we would expect roughly half of them (500) to have decayed, leaving 500 still remaining. After another 1620 years, half of those remaining 500 (250) would have decayed, leaving 250 still remaining, and so on. Similarly, if we start with 1000 atoms of the 405-year isotope, after 405 years we would expect roughly half of them (500) to have decayed, leaving 500 still remaining. After another 405 years, half of those remaining 500 (250) would have decayed, leaving 250 still remaining, and so on.
For example, if we start with 1000 atoms of the 1620-year isotope, after 1620 years we would expect roughly half of them (500) to have decayed, leaving 500 still remaining. After another 1620 years, half of those remaining 500 (250) would have decayed, leaving 250 still remaining, and so on. Similarly, if we start with 1000 atoms of the 405-year isotope, after 405 years we would expect roughly half of them (500) to have decayed, leaving 500 still remaining. After another 405 years, half of those remaining 500 (250) would have decayed, leaving 250 still remaining, and so on.
|
Explore Courses for JEE exam
|
|
Top Courses for JEEView all
The mean lives of a radioactive substance are 1620 years and 405 years for α - emission and β - emission respectively. Find the time during which three-fourth of a sample will decay if it is decaying both by α – emission and β – emission simultaneously.a)449 yearsb)450 yearsc)365 yearsd)439 yearsCorrect answer is option 'A'. Can you explain this answer?
Question Description
The mean lives of a radioactive substance are 1620 years and 405 years for α - emission and β - emission respectively. Find the time during which three-fourth of a sample will decay if it is decaying both by α – emission and β – emission simultaneously.a)449 yearsb)450 yearsc)365 yearsd)439 yearsCorrect answer is option 'A'. Can you explain this answer? for JEE 2025 is part of JEE preparation. The Question and answers have been prepared according to the JEE exam syllabus. Information about The mean lives of a radioactive substance are 1620 years and 405 years for α - emission and β - emission respectively. Find the time during which three-fourth of a sample will decay if it is decaying both by α – emission and β – emission simultaneously.a)449 yearsb)450 yearsc)365 yearsd)439 yearsCorrect answer is option 'A'. Can you explain this answer? covers all topics & solutions for JEE 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for The mean lives of a radioactive substance are 1620 years and 405 years for α - emission and β - emission respectively. Find the time during which three-fourth of a sample will decay if it is decaying both by α – emission and β – emission simultaneously.a)449 yearsb)450 yearsc)365 yearsd)439 yearsCorrect answer is option 'A'. Can you explain this answer?.
The mean lives of a radioactive substance are 1620 years and 405 years for α - emission and β - emission respectively. Find the time during which three-fourth of a sample will decay if it is decaying both by α – emission and β – emission simultaneously.a)449 yearsb)450 yearsc)365 yearsd)439 yearsCorrect answer is option 'A'. Can you explain this answer? for JEE 2025 is part of JEE preparation. The Question and answers have been prepared according to the JEE exam syllabus. Information about The mean lives of a radioactive substance are 1620 years and 405 years for α - emission and β - emission respectively. Find the time during which three-fourth of a sample will decay if it is decaying both by α – emission and β – emission simultaneously.a)449 yearsb)450 yearsc)365 yearsd)439 yearsCorrect answer is option 'A'. Can you explain this answer? covers all topics & solutions for JEE 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for The mean lives of a radioactive substance are 1620 years and 405 years for α - emission and β - emission respectively. Find the time during which three-fourth of a sample will decay if it is decaying both by α – emission and β – emission simultaneously.a)449 yearsb)450 yearsc)365 yearsd)439 yearsCorrect answer is option 'A'. Can you explain this answer?.
Solutions for The mean lives of a radioactive substance are 1620 years and 405 years for α - emission and β - emission respectively. Find the time during which three-fourth of a sample will decay if it is decaying both by α – emission and β – emission simultaneously.a)449 yearsb)450 yearsc)365 yearsd)439 yearsCorrect answer is option 'A'. Can you explain this answer? in English & in Hindi are available as part of our courses for JEE.
Download more important topics, notes, lectures and mock test series for JEE Exam by signing up for free.
Here you can find the meaning of The mean lives of a radioactive substance are 1620 years and 405 years for α - emission and β - emission respectively. Find the time during which three-fourth of a sample will decay if it is decaying both by α – emission and β – emission simultaneously.a)449 yearsb)450 yearsc)365 yearsd)439 yearsCorrect answer is option 'A'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
The mean lives of a radioactive substance are 1620 years and 405 years for α - emission and β - emission respectively. Find the time during which three-fourth of a sample will decay if it is decaying both by α – emission and β – emission simultaneously.a)449 yearsb)450 yearsc)365 yearsd)439 yearsCorrect answer is option 'A'. Can you explain this answer?, a detailed solution for The mean lives of a radioactive substance are 1620 years and 405 years for α - emission and β - emission respectively. Find the time during which three-fourth of a sample will decay if it is decaying both by α – emission and β – emission simultaneously.a)449 yearsb)450 yearsc)365 yearsd)439 yearsCorrect answer is option 'A'. Can you explain this answer? has been provided alongside types of The mean lives of a radioactive substance are 1620 years and 405 years for α - emission and β - emission respectively. Find the time during which three-fourth of a sample will decay if it is decaying both by α – emission and β – emission simultaneously.a)449 yearsb)450 yearsc)365 yearsd)439 yearsCorrect answer is option 'A'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice The mean lives of a radioactive substance are 1620 years and 405 years for α - emission and β - emission respectively. Find the time during which three-fourth of a sample will decay if it is decaying both by α – emission and β – emission simultaneously.a)449 yearsb)450 yearsc)365 yearsd)439 yearsCorrect answer is option 'A'. Can you explain this answer? tests, examples and also practice JEE tests.
|
|
Explore Courses for JEE exam
|
|
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.
|
© EduRev
|
Education Revolution
|
|
Signup to see your scores
go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup