Class 11 Exam > Class 11 Questions > An open cubical tank was initially fully fill...
Start Learning for Free
An open cubical tank was initially fully filled with water. When the tank was accelerated on a horizontal plane along one of its side it was found that one third of volume of water spilled out. The acceleration was
- a)g/4
- b)g/3
- c)3g/2
- d)None
Correct answer is option 'B'. Can you explain this answer?
| FREE This question is part of | Download PDF Attempt this Test |
Verified Answer
An open cubical tank was initially fully filled with water. When the t...
Let say the tank is accelerating by some acceleration a, such that the rest water in the tanks forms shape like this -
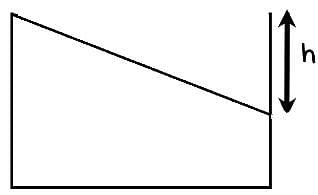
Acceleration, a is right wards.
Where let say h is the height from top till which there is no water
Now if we say V is total volume and B is area of its base and S be its height
We have ½ h X B = V / 3
Thus we get h = S/3
Thus the angle in this cross section of vacant triangle is tan-1 ⅓
Also the same triangle relates a and g, which can be seen when we make the block a inertial frame by adding pseudo force of magnitude ma and directing leftwards, thus we get a/g = ⅓
Thus we get a = g/3

Acceleration, a is right wards.
Where let say h is the height from top till which there is no water
Now if we say V is total volume and B is area of its base and S be its height
We have ½ h X B = V / 3
Thus we get h = S/3
Thus the angle in this cross section of vacant triangle is tan-1 ⅓
Also the same triangle relates a and g, which can be seen when we make the block a inertial frame by adding pseudo force of magnitude ma and directing leftwards, thus we get a/g = ⅓
Thus we get a = g/3
Most Upvoted Answer
An open cubical tank was initially fully filled with water. When the t...
Understanding the problem:
We are given an open cubical tank filled with water and placed on a horizontal plane. When the tank is accelerated along one of its sides, one-third of the volume of water spills out. We need to determine the acceleration of the tank.
Key concepts:
1. Density: The density of a substance is defined as the mass per unit volume. In this problem, the density of water will be used to solve the problem.
2. Buoyancy: When an object is placed in a fluid, it experiences an upward force called buoyant force. The magnitude of this force is equal to the weight of the fluid displaced by the object.
3. Archimedes' principle: It states that an object immersed in a fluid experiences an upward buoyant force equal to the weight of the fluid it displaces.
Solution:
Let's solve the problem step by step:
Step 1: Determine the initial volume of water in the tank.
Since the tank is initially fully filled with water, the initial volume of water in the tank is equal to the volume of the tank.
Step 2: Determine the volume of water spilled out.
Given that one-third of the volume of water spills out when the tank is accelerated, we can calculate the volume of water spilled out as follows:
Volume of water spilled out = (1/3) * Initial volume of water
Step 3: Determine the weight of the water spilled out.
The weight of an object is given by the product of its mass and the acceleration due to gravity.
Weight of water spilled out = Density of water * Volume of water spilled out * Acceleration due to gravity
Step 4: Determine the buoyant force acting on the tank.
Since the tank is open, the water spilled out will displace an equal volume of water. Therefore, the buoyant force acting on the tank will be equal to the weight of water spilled out.
Step 5: Equate the weight of water spilled out to the buoyant force.
Since the tank is in equilibrium, the weight of water spilled out will be balanced by the buoyant force.
Weight of water spilled out = Buoyant force
Step 6: Substitute the values and solve for acceleration.
By substituting the expressions for the weight of water spilled out and the buoyant force, we can solve for the acceleration of the tank.
Density of water * Volume of water spilled out * Acceleration due to gravity = Density of water * Volume of water spilled out * Acceleration of the tank
Step 7: Simplify the equation to find the acceleration.
By canceling out the factors of density and volume of water spilled out, we can determine the value of the acceleration.
Acceleration due to gravity = Acceleration of the tank
Step 8: Substitute the known value for acceleration due to gravity and solve for the acceleration of the tank.
By substituting the value of acceleration due to gravity (g) into the equation, we can solve for the acceleration of the tank.
Acceleration due to gravity = g
Acceleration of the tank = g
Therefore, the correct answer is option B: g/3.
We are given an open cubical tank filled with water and placed on a horizontal plane. When the tank is accelerated along one of its sides, one-third of the volume of water spills out. We need to determine the acceleration of the tank.
Key concepts:
1. Density: The density of a substance is defined as the mass per unit volume. In this problem, the density of water will be used to solve the problem.
2. Buoyancy: When an object is placed in a fluid, it experiences an upward force called buoyant force. The magnitude of this force is equal to the weight of the fluid displaced by the object.
3. Archimedes' principle: It states that an object immersed in a fluid experiences an upward buoyant force equal to the weight of the fluid it displaces.
Solution:
Let's solve the problem step by step:
Step 1: Determine the initial volume of water in the tank.
Since the tank is initially fully filled with water, the initial volume of water in the tank is equal to the volume of the tank.
Step 2: Determine the volume of water spilled out.
Given that one-third of the volume of water spills out when the tank is accelerated, we can calculate the volume of water spilled out as follows:
Volume of water spilled out = (1/3) * Initial volume of water
Step 3: Determine the weight of the water spilled out.
The weight of an object is given by the product of its mass and the acceleration due to gravity.
Weight of water spilled out = Density of water * Volume of water spilled out * Acceleration due to gravity
Step 4: Determine the buoyant force acting on the tank.
Since the tank is open, the water spilled out will displace an equal volume of water. Therefore, the buoyant force acting on the tank will be equal to the weight of water spilled out.
Step 5: Equate the weight of water spilled out to the buoyant force.
Since the tank is in equilibrium, the weight of water spilled out will be balanced by the buoyant force.
Weight of water spilled out = Buoyant force
Step 6: Substitute the values and solve for acceleration.
By substituting the expressions for the weight of water spilled out and the buoyant force, we can solve for the acceleration of the tank.
Density of water * Volume of water spilled out * Acceleration due to gravity = Density of water * Volume of water spilled out * Acceleration of the tank
Step 7: Simplify the equation to find the acceleration.
By canceling out the factors of density and volume of water spilled out, we can determine the value of the acceleration.
Acceleration due to gravity = Acceleration of the tank
Step 8: Substitute the known value for acceleration due to gravity and solve for the acceleration of the tank.
By substituting the value of acceleration due to gravity (g) into the equation, we can solve for the acceleration of the tank.
Acceleration due to gravity = g
Acceleration of the tank = g
Therefore, the correct answer is option B: g/3.
Attention Class 11 Students!
To make sure you are not studying endlessly, EduRev has designed Class 11 study material, with Structured Courses, Videos, & Test Series. Plus get personalized analysis, doubt solving and improvement plans to achieve a great score in Class 11.

|
Explore Courses for Class 11 exam
|

|
Similar Class 11 Doubts
An open cubical tank was initially fully filled with water. When the tank was accelerated on a horizontal plane along one of its side it was found that one third of volume of water spilled out. The acceleration wasa)g/4b)g/3c)3g/2d)NoneCorrect answer is option 'B'. Can you explain this answer?
Question Description
An open cubical tank was initially fully filled with water. When the tank was accelerated on a horizontal plane along one of its side it was found that one third of volume of water spilled out. The acceleration wasa)g/4b)g/3c)3g/2d)NoneCorrect answer is option 'B'. Can you explain this answer? for Class 11 2024 is part of Class 11 preparation. The Question and answers have been prepared according to the Class 11 exam syllabus. Information about An open cubical tank was initially fully filled with water. When the tank was accelerated on a horizontal plane along one of its side it was found that one third of volume of water spilled out. The acceleration wasa)g/4b)g/3c)3g/2d)NoneCorrect answer is option 'B'. Can you explain this answer? covers all topics & solutions for Class 11 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for An open cubical tank was initially fully filled with water. When the tank was accelerated on a horizontal plane along one of its side it was found that one third of volume of water spilled out. The acceleration wasa)g/4b)g/3c)3g/2d)NoneCorrect answer is option 'B'. Can you explain this answer?.
An open cubical tank was initially fully filled with water. When the tank was accelerated on a horizontal plane along one of its side it was found that one third of volume of water spilled out. The acceleration wasa)g/4b)g/3c)3g/2d)NoneCorrect answer is option 'B'. Can you explain this answer? for Class 11 2024 is part of Class 11 preparation. The Question and answers have been prepared according to the Class 11 exam syllabus. Information about An open cubical tank was initially fully filled with water. When the tank was accelerated on a horizontal plane along one of its side it was found that one third of volume of water spilled out. The acceleration wasa)g/4b)g/3c)3g/2d)NoneCorrect answer is option 'B'. Can you explain this answer? covers all topics & solutions for Class 11 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for An open cubical tank was initially fully filled with water. When the tank was accelerated on a horizontal plane along one of its side it was found that one third of volume of water spilled out. The acceleration wasa)g/4b)g/3c)3g/2d)NoneCorrect answer is option 'B'. Can you explain this answer?.
Solutions for An open cubical tank was initially fully filled with water. When the tank was accelerated on a horizontal plane along one of its side it was found that one third of volume of water spilled out. The acceleration wasa)g/4b)g/3c)3g/2d)NoneCorrect answer is option 'B'. Can you explain this answer? in English & in Hindi are available as part of our courses for Class 11.
Download more important topics, notes, lectures and mock test series for Class 11 Exam by signing up for free.
Here you can find the meaning of An open cubical tank was initially fully filled with water. When the tank was accelerated on a horizontal plane along one of its side it was found that one third of volume of water spilled out. The acceleration wasa)g/4b)g/3c)3g/2d)NoneCorrect answer is option 'B'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
An open cubical tank was initially fully filled with water. When the tank was accelerated on a horizontal plane along one of its side it was found that one third of volume of water spilled out. The acceleration wasa)g/4b)g/3c)3g/2d)NoneCorrect answer is option 'B'. Can you explain this answer?, a detailed solution for An open cubical tank was initially fully filled with water. When the tank was accelerated on a horizontal plane along one of its side it was found that one third of volume of water spilled out. The acceleration wasa)g/4b)g/3c)3g/2d)NoneCorrect answer is option 'B'. Can you explain this answer? has been provided alongside types of An open cubical tank was initially fully filled with water. When the tank was accelerated on a horizontal plane along one of its side it was found that one third of volume of water spilled out. The acceleration wasa)g/4b)g/3c)3g/2d)NoneCorrect answer is option 'B'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice An open cubical tank was initially fully filled with water. When the tank was accelerated on a horizontal plane along one of its side it was found that one third of volume of water spilled out. The acceleration wasa)g/4b)g/3c)3g/2d)NoneCorrect answer is option 'B'. Can you explain this answer? tests, examples and also practice Class 11 tests.

|
Explore Courses for Class 11 exam
|

|
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.
























