Mathematics Exam > Mathematics Questions > The planer region bounded by the parabola y =...
Start Learning for Free
The planer region bounded by the parabola y = 2x2 + 3, the x - axis and by the lines x = 0 and x = 1 revolves about the y - axis. The volume of the solid of revolution generated is _________ .
Correct answer is '12.566'. Can you explain this answer?
| FREE This question is part of | Download PDF Attempt this Test |
Verified Answer
The planer region bounded by the parabola y = 2x2 + 3, the x - axis an...
Divide the area of the figure into elementary strip by straight lines parallel to the y-axis.
Hence, generated volume is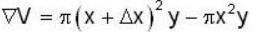
Hence volume dV = 2πxydx
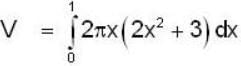
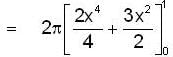

Hence, generated volume is
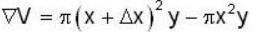
Hence volume dV = 2πxydx
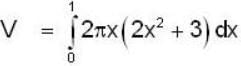
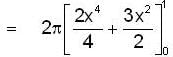

Most Upvoted Answer
The planer region bounded by the parabola y = 2x2 + 3, the x - axis an...
To find the volume of the solid of revolution generated by revolving the planar region bounded by the parabola y = 2x^2 - 3, the x-axis, and the lines x = 0 and x = 1 about the y-axis, we can use the method of cylindrical shells.
Step 1: Sketching the region
First, let's sketch the given region in the xy-plane. The parabola y = 2x^2 - 3 is symmetric with respect to the y-axis and opens upwards. It intersects the x-axis at x = ±√(3/2). The region is bounded by the parabola, the x-axis, and the vertical lines x = 0 and x = 1.
Step 2: Determining the height of the cylindrical shells
The height of each cylindrical shell is given by the difference in the y-values of the parabola at the corresponding x-values. The equation of the parabola is y = 2x^2 - 3.
At x = 0, the height of the shell is y = 2(0)^2 - 3 = -3.
At x = 1, the height of the shell is y = 2(1)^2 - 3 = -1.
So, the height of each cylindrical shell varies from -3 to -1.
Step 3: Determining the radius of the cylindrical shells
The radius of each cylindrical shell is given by the corresponding x-value. Since the shells are being revolved about the y-axis, the radius is the distance from the y-axis to the parabola at each x-value.
At x = 0, the radius of the shell is 0.
At x = 1, the radius of the shell is 1.
So, the radius of each cylindrical shell varies from 0 to 1.
Step 4: Calculating the volume of each cylindrical shell
The volume of each cylindrical shell is given by the formula V = 2πrh, where r is the radius and h is the height.
For this problem, the radius and height of each shell vary depending on the x-value. So, we need to integrate the volume of each shell over the interval [0, 1].
The integral for the volume of each cylindrical shell is:
V = ∫[0,1] 2πx(2x^2 - 3) dx
Simplifying the integral:
V = 2π ∫[0,1] (2x^3 - 3x) dx
= 2π [∫(2x^3) dx - ∫(3x) dx]
= 2π [x^4 - (3/2)x^2] evaluated from x = 0 to x = 1
= 2π [(1^4 - (3/2)(1^2)) - (0^4 - (3/2)(0^2))]
= 2π [(1 - (3/2)) - (0 - 0)]
= 2π [(1/2)]
= π
Step 5: Final answer
The volume of the solid of revolution generated is π cubic units. Since the question asks for the
Step 1: Sketching the region
First, let's sketch the given region in the xy-plane. The parabola y = 2x^2 - 3 is symmetric with respect to the y-axis and opens upwards. It intersects the x-axis at x = ±√(3/2). The region is bounded by the parabola, the x-axis, and the vertical lines x = 0 and x = 1.
Step 2: Determining the height of the cylindrical shells
The height of each cylindrical shell is given by the difference in the y-values of the parabola at the corresponding x-values. The equation of the parabola is y = 2x^2 - 3.
At x = 0, the height of the shell is y = 2(0)^2 - 3 = -3.
At x = 1, the height of the shell is y = 2(1)^2 - 3 = -1.
So, the height of each cylindrical shell varies from -3 to -1.
Step 3: Determining the radius of the cylindrical shells
The radius of each cylindrical shell is given by the corresponding x-value. Since the shells are being revolved about the y-axis, the radius is the distance from the y-axis to the parabola at each x-value.
At x = 0, the radius of the shell is 0.
At x = 1, the radius of the shell is 1.
So, the radius of each cylindrical shell varies from 0 to 1.
Step 4: Calculating the volume of each cylindrical shell
The volume of each cylindrical shell is given by the formula V = 2πrh, where r is the radius and h is the height.
For this problem, the radius and height of each shell vary depending on the x-value. So, we need to integrate the volume of each shell over the interval [0, 1].
The integral for the volume of each cylindrical shell is:
V = ∫[0,1] 2πx(2x^2 - 3) dx
Simplifying the integral:
V = 2π ∫[0,1] (2x^3 - 3x) dx
= 2π [∫(2x^3) dx - ∫(3x) dx]
= 2π [x^4 - (3/2)x^2] evaluated from x = 0 to x = 1
= 2π [(1^4 - (3/2)(1^2)) - (0^4 - (3/2)(0^2))]
= 2π [(1 - (3/2)) - (0 - 0)]
= 2π [(1/2)]
= π
Step 5: Final answer
The volume of the solid of revolution generated is π cubic units. Since the question asks for the
Free Test
FREE
| Start Free Test |
Community Answer
The planer region bounded by the parabola y = 2x2 + 3, the x - axis an...
Divide the area of the figure into elementary strip by straight lines parallel to the y-axis.
Hence, generated volume is
Hence volume dV = 2πxydx

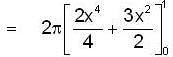

Hence, generated volume is
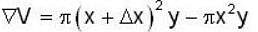
Hence volume dV = 2πxydx

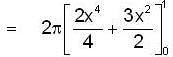


|
Explore Courses for Mathematics exam
|

|
The planer region bounded by the parabola y = 2x2 + 3, the x - axis and by the lines x = 0 and x = 1 revolves about the y - axis. The volume of the solid of revolution generated is _________ .Correct answer is '12.566'. Can you explain this answer?
Question Description
The planer region bounded by the parabola y = 2x2 + 3, the x - axis and by the lines x = 0 and x = 1 revolves about the y - axis. The volume of the solid of revolution generated is _________ .Correct answer is '12.566'. Can you explain this answer? for Mathematics 2024 is part of Mathematics preparation. The Question and answers have been prepared according to the Mathematics exam syllabus. Information about The planer region bounded by the parabola y = 2x2 + 3, the x - axis and by the lines x = 0 and x = 1 revolves about the y - axis. The volume of the solid of revolution generated is _________ .Correct answer is '12.566'. Can you explain this answer? covers all topics & solutions for Mathematics 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for The planer region bounded by the parabola y = 2x2 + 3, the x - axis and by the lines x = 0 and x = 1 revolves about the y - axis. The volume of the solid of revolution generated is _________ .Correct answer is '12.566'. Can you explain this answer?.
The planer region bounded by the parabola y = 2x2 + 3, the x - axis and by the lines x = 0 and x = 1 revolves about the y - axis. The volume of the solid of revolution generated is _________ .Correct answer is '12.566'. Can you explain this answer? for Mathematics 2024 is part of Mathematics preparation. The Question and answers have been prepared according to the Mathematics exam syllabus. Information about The planer region bounded by the parabola y = 2x2 + 3, the x - axis and by the lines x = 0 and x = 1 revolves about the y - axis. The volume of the solid of revolution generated is _________ .Correct answer is '12.566'. Can you explain this answer? covers all topics & solutions for Mathematics 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for The planer region bounded by the parabola y = 2x2 + 3, the x - axis and by the lines x = 0 and x = 1 revolves about the y - axis. The volume of the solid of revolution generated is _________ .Correct answer is '12.566'. Can you explain this answer?.
Solutions for The planer region bounded by the parabola y = 2x2 + 3, the x - axis and by the lines x = 0 and x = 1 revolves about the y - axis. The volume of the solid of revolution generated is _________ .Correct answer is '12.566'. Can you explain this answer? in English & in Hindi are available as part of our courses for Mathematics.
Download more important topics, notes, lectures and mock test series for Mathematics Exam by signing up for free.
Here you can find the meaning of The planer region bounded by the parabola y = 2x2 + 3, the x - axis and by the lines x = 0 and x = 1 revolves about the y - axis. The volume of the solid of revolution generated is _________ .Correct answer is '12.566'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
The planer region bounded by the parabola y = 2x2 + 3, the x - axis and by the lines x = 0 and x = 1 revolves about the y - axis. The volume of the solid of revolution generated is _________ .Correct answer is '12.566'. Can you explain this answer?, a detailed solution for The planer region bounded by the parabola y = 2x2 + 3, the x - axis and by the lines x = 0 and x = 1 revolves about the y - axis. The volume of the solid of revolution generated is _________ .Correct answer is '12.566'. Can you explain this answer? has been provided alongside types of The planer region bounded by the parabola y = 2x2 + 3, the x - axis and by the lines x = 0 and x = 1 revolves about the y - axis. The volume of the solid of revolution generated is _________ .Correct answer is '12.566'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice The planer region bounded by the parabola y = 2x2 + 3, the x - axis and by the lines x = 0 and x = 1 revolves about the y - axis. The volume of the solid of revolution generated is _________ .Correct answer is '12.566'. Can you explain this answer? tests, examples and also practice Mathematics tests.

|
Explore Courses for Mathematics exam
|

|
Suggested Free Tests
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.
















