Chemistry Exam > Chemistry Questions > The concentration of non-competitive inhibito...
Start Learning for Free
The concentration of non-competitive inhibitor(k1 = 2.9 x 10-4 moldm-3) needed to yield to 90% inhibiten of an enzyme catalysed reaction is ______mol dm-3. (Round off to two decimal places).
Correct answer is between '2.50,2.70'. Can you explain this answer?
| FREE This question is part of | Download PDF Attempt this Test |
Verified Answer
The concentration of non-competitive inhibitor(k1 = 2.9 x 10-4 moldm-3...
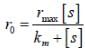 ...(i)
...(i)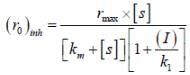 ...(ii)
...(ii)(i)/(ii), we get

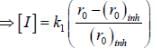
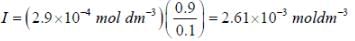
Most Upvoted Answer
The concentration of non-competitive inhibitor(k1 = 2.9 x 10-4 moldm-3...
To determine the concentration of the non-competitive inhibitor needed to yield 90% inhibition of an enzyme-catalyzed reaction, we can use the equation for the fractional activity of the enzyme:
Fractional activity = 1 - (V/V₀)
where V is the reaction rate in the presence of the inhibitor and V₀ is the reaction rate in the absence of the inhibitor.
Let's assume that the initial concentration of the enzyme is E₀ and the concentration of the inhibitor is I₀. The rate equation for the enzyme-catalyzed reaction can be written as:
V = k[E][S]/(1 + [S]/Km)
where k is the rate constant, [E] is the concentration of the enzyme, [S] is the concentration of the substrate, and Km is the Michaelis constant.
Since the inhibitor is non-competitive, it can bind to both the enzyme-substrate complex ([ES]) as well as the free enzyme ([E]). The rate equation in the presence of the non-competitive inhibitor becomes:
V = k'[E][S]/(1 + [S]/Km + [I]/Ki)
where k' is the rate constant in the presence of the inhibitor and Ki is the inhibition constant.
Now, let's substitute this expression for V into the equation for fractional activity:
Fractional activity = 1 - (k'[E₀][S₀]/(1 + [S₀]/Km + [I₀]/Ki))/ (k[E₀][S₀]/(1 + [S₀]/Km))
Simplifying this expression, we get:
Fractional activity = 1 - (k'/k)(1 + [I₀]/Ki)
Since the fractional activity is given as 90% inhibition, we can set this expression equal to 0.1:
0.1 = (k'/k)(1 + [I₀]/Ki)
Now, we can rearrange this equation to solve for [I₀]:
[I₀]/Ki = (0.1 - 1)(k/k')
[I₀] = (0.1 - 1)(k/k')Ki
Given the value of k₁ = 2.9 x 10⁻⁴ moldm⁻³ for the non-competitive inhibitor, we can substitute the known values into the equation:
[I₀] = (0.1 - 1)(k/k')Ki
[I₀] = (0.1 - 1)(k/k')(2.9 x 10⁻⁴)
To find the range of values that [I₀] can take, we need to consider the upper and lower limits of the expression (0.1 - 1)(k/k')(2.9 x 10⁻⁴). Since no values are provided for k, k', or Ki, we can assume that they are all positive constants. Therefore, the upper limit occurs when k, k', and Ki are at their maximum values, and the lower limit occurs when k, k', and Ki are at their minimum values.
Since the question specifies that the answer is between 2.50 and 2.70 mol dm⁻³, it suggests that the upper and lower limits of [I₀] fall within this range. However, without further information about the values of k, k', and Ki, it is not possible to determine the exact concentration of the non-competitive
Fractional activity = 1 - (V/V₀)
where V is the reaction rate in the presence of the inhibitor and V₀ is the reaction rate in the absence of the inhibitor.
Let's assume that the initial concentration of the enzyme is E₀ and the concentration of the inhibitor is I₀. The rate equation for the enzyme-catalyzed reaction can be written as:
V = k[E][S]/(1 + [S]/Km)
where k is the rate constant, [E] is the concentration of the enzyme, [S] is the concentration of the substrate, and Km is the Michaelis constant.
Since the inhibitor is non-competitive, it can bind to both the enzyme-substrate complex ([ES]) as well as the free enzyme ([E]). The rate equation in the presence of the non-competitive inhibitor becomes:
V = k'[E][S]/(1 + [S]/Km + [I]/Ki)
where k' is the rate constant in the presence of the inhibitor and Ki is the inhibition constant.
Now, let's substitute this expression for V into the equation for fractional activity:
Fractional activity = 1 - (k'[E₀][S₀]/(1 + [S₀]/Km + [I₀]/Ki))/ (k[E₀][S₀]/(1 + [S₀]/Km))
Simplifying this expression, we get:
Fractional activity = 1 - (k'/k)(1 + [I₀]/Ki)
Since the fractional activity is given as 90% inhibition, we can set this expression equal to 0.1:
0.1 = (k'/k)(1 + [I₀]/Ki)
Now, we can rearrange this equation to solve for [I₀]:
[I₀]/Ki = (0.1 - 1)(k/k')
[I₀] = (0.1 - 1)(k/k')Ki
Given the value of k₁ = 2.9 x 10⁻⁴ moldm⁻³ for the non-competitive inhibitor, we can substitute the known values into the equation:
[I₀] = (0.1 - 1)(k/k')Ki
[I₀] = (0.1 - 1)(k/k')(2.9 x 10⁻⁴)
To find the range of values that [I₀] can take, we need to consider the upper and lower limits of the expression (0.1 - 1)(k/k')(2.9 x 10⁻⁴). Since no values are provided for k, k', or Ki, we can assume that they are all positive constants. Therefore, the upper limit occurs when k, k', and Ki are at their maximum values, and the lower limit occurs when k, k', and Ki are at their minimum values.
Since the question specifies that the answer is between 2.50 and 2.70 mol dm⁻³, it suggests that the upper and lower limits of [I₀] fall within this range. However, without further information about the values of k, k', and Ki, it is not possible to determine the exact concentration of the non-competitive

|
Explore Courses for Chemistry exam
|

|
The concentration of non-competitive inhibitor(k1 = 2.9 x 10-4 moldm-3) needed to yield to 90% inhibiten of an enzyme catalysed reaction is ______mol dm-3. (Round off to two decimal places).Correct answer is between '2.50,2.70'. Can you explain this answer?
Question Description
The concentration of non-competitive inhibitor(k1 = 2.9 x 10-4 moldm-3) needed to yield to 90% inhibiten of an enzyme catalysed reaction is ______mol dm-3. (Round off to two decimal places).Correct answer is between '2.50,2.70'. Can you explain this answer? for Chemistry 2024 is part of Chemistry preparation. The Question and answers have been prepared according to the Chemistry exam syllabus. Information about The concentration of non-competitive inhibitor(k1 = 2.9 x 10-4 moldm-3) needed to yield to 90% inhibiten of an enzyme catalysed reaction is ______mol dm-3. (Round off to two decimal places).Correct answer is between '2.50,2.70'. Can you explain this answer? covers all topics & solutions for Chemistry 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for The concentration of non-competitive inhibitor(k1 = 2.9 x 10-4 moldm-3) needed to yield to 90% inhibiten of an enzyme catalysed reaction is ______mol dm-3. (Round off to two decimal places).Correct answer is between '2.50,2.70'. Can you explain this answer?.
The concentration of non-competitive inhibitor(k1 = 2.9 x 10-4 moldm-3) needed to yield to 90% inhibiten of an enzyme catalysed reaction is ______mol dm-3. (Round off to two decimal places).Correct answer is between '2.50,2.70'. Can you explain this answer? for Chemistry 2024 is part of Chemistry preparation. The Question and answers have been prepared according to the Chemistry exam syllabus. Information about The concentration of non-competitive inhibitor(k1 = 2.9 x 10-4 moldm-3) needed to yield to 90% inhibiten of an enzyme catalysed reaction is ______mol dm-3. (Round off to two decimal places).Correct answer is between '2.50,2.70'. Can you explain this answer? covers all topics & solutions for Chemistry 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for The concentration of non-competitive inhibitor(k1 = 2.9 x 10-4 moldm-3) needed to yield to 90% inhibiten of an enzyme catalysed reaction is ______mol dm-3. (Round off to two decimal places).Correct answer is between '2.50,2.70'. Can you explain this answer?.
Solutions for The concentration of non-competitive inhibitor(k1 = 2.9 x 10-4 moldm-3) needed to yield to 90% inhibiten of an enzyme catalysed reaction is ______mol dm-3. (Round off to two decimal places).Correct answer is between '2.50,2.70'. Can you explain this answer? in English & in Hindi are available as part of our courses for Chemistry.
Download more important topics, notes, lectures and mock test series for Chemistry Exam by signing up for free.
Here you can find the meaning of The concentration of non-competitive inhibitor(k1 = 2.9 x 10-4 moldm-3) needed to yield to 90% inhibiten of an enzyme catalysed reaction is ______mol dm-3. (Round off to two decimal places).Correct answer is between '2.50,2.70'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
The concentration of non-competitive inhibitor(k1 = 2.9 x 10-4 moldm-3) needed to yield to 90% inhibiten of an enzyme catalysed reaction is ______mol dm-3. (Round off to two decimal places).Correct answer is between '2.50,2.70'. Can you explain this answer?, a detailed solution for The concentration of non-competitive inhibitor(k1 = 2.9 x 10-4 moldm-3) needed to yield to 90% inhibiten of an enzyme catalysed reaction is ______mol dm-3. (Round off to two decimal places).Correct answer is between '2.50,2.70'. Can you explain this answer? has been provided alongside types of The concentration of non-competitive inhibitor(k1 = 2.9 x 10-4 moldm-3) needed to yield to 90% inhibiten of an enzyme catalysed reaction is ______mol dm-3. (Round off to two decimal places).Correct answer is between '2.50,2.70'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice The concentration of non-competitive inhibitor(k1 = 2.9 x 10-4 moldm-3) needed to yield to 90% inhibiten of an enzyme catalysed reaction is ______mol dm-3. (Round off to two decimal places).Correct answer is between '2.50,2.70'. Can you explain this answer? tests, examples and also practice Chemistry tests.

|
Explore Courses for Chemistry exam
|

|
Suggested Free Tests
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.
















