Mechanical Engineering Exam > Mechanical Engineering Questions > Stokes theorem connects a)A line integral and...
Start Learning for Free
Stokes theorem connects
- a)A line integral and a surface integral
- b)A surface integral and a volume integral
- c)A line integral and a volume integral
- d)Gradient of a function and its surface integral
Correct answer is option 'A'. Can you explain this answer?
Most Upvoted Answer
Stokes theorem connects a)A line integral and a surface integral b)A s...
Answer : 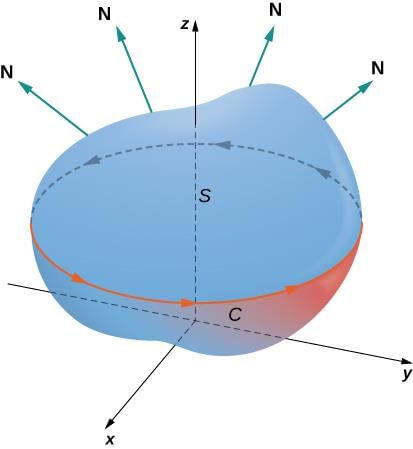
a)
A line integral and a surface integral
Stokes' theorem relates a vector surface integral over surface S in space to a line integral around the boundary of S. ... In addition to allowing us to translate between line integrals and surface integrals, Stokes' theorem connects the concepts of curl and circulation.

Free Test
FREE
| Start Free Test |
Community Answer
Stokes theorem connects a)A line integral and a surface integral b)A s...
Stokes' theorem connects a line integral and a surface integral.
Introduction:
Stokes' theorem is a fundamental theorem in vector calculus that relates a line integral around a closed curve to a surface integral over the region bounded by that curve. It provides a powerful tool for calculating circulations and fluxes in vector fields.
Statement of Stokes' theorem:
Stokes' theorem states that the line integral of a vector field F around a closed curve C is equal to the surface integral of the curl of F over the surface S bounded by C. Mathematically, it can be written as:
∮C F · dr = ∬S (curl F) · dS
where ∮C represents the line integral around the closed curve C, F is the vector field, dr is an infinitesimal vector along the curve C, ∬S represents the surface integral over the surface S, curl F is the curl of the vector field F, and dS is an infinitesimal vector normal to the surface S.
Explanation:
Stokes' theorem connects a line integral and a surface integral by relating the circulation of a vector field around a closed curve to the flux of its curl through the surface bounded by that curve. Here's a step-by-step explanation of how it works:
1. Consider a closed curve C in a vector field F.
2. Divide the surface bounded by the curve C into infinitesimal surface elements.
3. Calculate the curl of the vector field F at each point on the surface.
4. Take the dot product of the curl of F with the infinitesimal vector normal to the surface at each point.
5. Sum up all the dot products over the entire surface to obtain the surface integral of the curl of F.
6. Calculate the line integral of the vector field F along the closed curve C.
7. According to Stokes' theorem, the line integral is equal to the surface integral.
Significance:
Stokes' theorem provides a powerful tool for calculating the circulation of a vector field around a closed curve or the flux of its curl through a surface. It allows us to relate these two seemingly different concepts and provides a bridge between line integrals and surface integrals. This theorem has applications in various fields, including fluid dynamics, electromagnetism, and differential geometry.
Introduction:
Stokes' theorem is a fundamental theorem in vector calculus that relates a line integral around a closed curve to a surface integral over the region bounded by that curve. It provides a powerful tool for calculating circulations and fluxes in vector fields.
Statement of Stokes' theorem:
Stokes' theorem states that the line integral of a vector field F around a closed curve C is equal to the surface integral of the curl of F over the surface S bounded by C. Mathematically, it can be written as:
∮C F · dr = ∬S (curl F) · dS
where ∮C represents the line integral around the closed curve C, F is the vector field, dr is an infinitesimal vector along the curve C, ∬S represents the surface integral over the surface S, curl F is the curl of the vector field F, and dS is an infinitesimal vector normal to the surface S.
Explanation:
Stokes' theorem connects a line integral and a surface integral by relating the circulation of a vector field around a closed curve to the flux of its curl through the surface bounded by that curve. Here's a step-by-step explanation of how it works:
1. Consider a closed curve C in a vector field F.
2. Divide the surface bounded by the curve C into infinitesimal surface elements.
3. Calculate the curl of the vector field F at each point on the surface.
4. Take the dot product of the curl of F with the infinitesimal vector normal to the surface at each point.
5. Sum up all the dot products over the entire surface to obtain the surface integral of the curl of F.
6. Calculate the line integral of the vector field F along the closed curve C.
7. According to Stokes' theorem, the line integral is equal to the surface integral.
Significance:
Stokes' theorem provides a powerful tool for calculating the circulation of a vector field around a closed curve or the flux of its curl through a surface. It allows us to relate these two seemingly different concepts and provides a bridge between line integrals and surface integrals. This theorem has applications in various fields, including fluid dynamics, electromagnetism, and differential geometry.

|
Explore Courses for Mechanical Engineering exam
|

|
Similar Mechanical Engineering Doubts
Stokes theorem connects a)A line integral and a surface integral b)A surface integral and a volume integralc)A line integral and a volume integral d)Gradient of a function and its surface integralCorrect answer is option 'A'. Can you explain this answer?
Question Description
Stokes theorem connects a)A line integral and a surface integral b)A surface integral and a volume integralc)A line integral and a volume integral d)Gradient of a function and its surface integralCorrect answer is option 'A'. Can you explain this answer? for Mechanical Engineering 2025 is part of Mechanical Engineering preparation. The Question and answers have been prepared according to the Mechanical Engineering exam syllabus. Information about Stokes theorem connects a)A line integral and a surface integral b)A surface integral and a volume integralc)A line integral and a volume integral d)Gradient of a function and its surface integralCorrect answer is option 'A'. Can you explain this answer? covers all topics & solutions for Mechanical Engineering 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for Stokes theorem connects a)A line integral and a surface integral b)A surface integral and a volume integralc)A line integral and a volume integral d)Gradient of a function and its surface integralCorrect answer is option 'A'. Can you explain this answer?.
Stokes theorem connects a)A line integral and a surface integral b)A surface integral and a volume integralc)A line integral and a volume integral d)Gradient of a function and its surface integralCorrect answer is option 'A'. Can you explain this answer? for Mechanical Engineering 2025 is part of Mechanical Engineering preparation. The Question and answers have been prepared according to the Mechanical Engineering exam syllabus. Information about Stokes theorem connects a)A line integral and a surface integral b)A surface integral and a volume integralc)A line integral and a volume integral d)Gradient of a function and its surface integralCorrect answer is option 'A'. Can you explain this answer? covers all topics & solutions for Mechanical Engineering 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for Stokes theorem connects a)A line integral and a surface integral b)A surface integral and a volume integralc)A line integral and a volume integral d)Gradient of a function and its surface integralCorrect answer is option 'A'. Can you explain this answer?.
Solutions for Stokes theorem connects a)A line integral and a surface integral b)A surface integral and a volume integralc)A line integral and a volume integral d)Gradient of a function and its surface integralCorrect answer is option 'A'. Can you explain this answer? in English & in Hindi are available as part of our courses for Mechanical Engineering.
Download more important topics, notes, lectures and mock test series for Mechanical Engineering Exam by signing up for free.
Here you can find the meaning of Stokes theorem connects a)A line integral and a surface integral b)A surface integral and a volume integralc)A line integral and a volume integral d)Gradient of a function and its surface integralCorrect answer is option 'A'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
Stokes theorem connects a)A line integral and a surface integral b)A surface integral and a volume integralc)A line integral and a volume integral d)Gradient of a function and its surface integralCorrect answer is option 'A'. Can you explain this answer?, a detailed solution for Stokes theorem connects a)A line integral and a surface integral b)A surface integral and a volume integralc)A line integral and a volume integral d)Gradient of a function and its surface integralCorrect answer is option 'A'. Can you explain this answer? has been provided alongside types of Stokes theorem connects a)A line integral and a surface integral b)A surface integral and a volume integralc)A line integral and a volume integral d)Gradient of a function and its surface integralCorrect answer is option 'A'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice Stokes theorem connects a)A line integral and a surface integral b)A surface integral and a volume integralc)A line integral and a volume integral d)Gradient of a function and its surface integralCorrect answer is option 'A'. Can you explain this answer? tests, examples and also practice Mechanical Engineering tests.

|
Explore Courses for Mechanical Engineering exam
|

|
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.


























