GATE Exam > GATE Questions > Consider a random walker on a square lattice....
Start Learning for Free
Consider a random walker on a square lattice. Walking to each neighbouring site is equally probable. The
probability that the walker is at a site which is only 2 steps away if he takes 4 steps in total is _____ (upto 2
decimal places)
probability that the walker is at a site which is only 2 steps away if he takes 4 steps in total is _____ (upto 2
decimal places)
Correct answer is between '0.44,0.48'. Can you explain this answer?
Verified Answer
Consider a random walker on a square lattice. Walking to each neighbou...
To effectively make only 2 steps, 1 out of the four steps lias to be in a direction opposite to one of the other 3.
Case-1 The walker takes a step back just after the 1 st step.
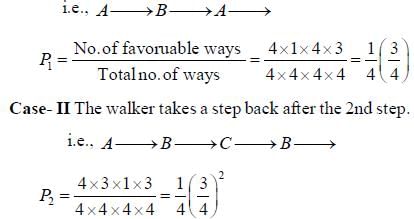
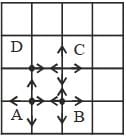
Case-1 The walker takes a step back just after the 1 st step.
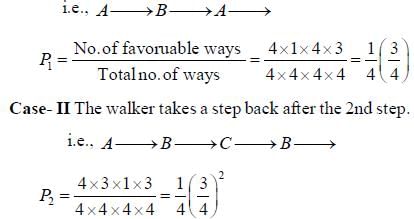

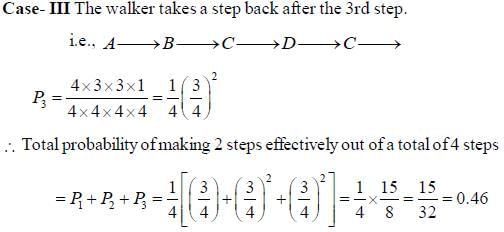
 This question is part of UPSC exam. View all GATE courses
This question is part of UPSC exam. View all GATE courses
Most Upvoted Answer
Consider a random walker on a square lattice. Walking to each neighbou...
Introduction: In this problem, we consider a random walker on a square lattice where the walker can take four steps in total. The probability that the walker is at a site which is only 2 steps away is to be determined.
Approach:
To solve this problem, we can consider the possible paths that the walker can take to reach a site which is only 2 steps away.
There are two possible ways to reach a site which is only 2 steps away:
1. The walker takes two steps in one direction, and then two steps in a perpendicular direction.
2. The walker takes one step in one direction, then turns 90 degrees and takes another step, then turns 180 degrees and takes a third step, and finally turns 90 degrees again and takes a fourth step.
Let us consider each of these cases separately:
Case 1: The walker takes two steps in one direction, and then two steps in a perpendicular direction.
In this case, there are two possible directions in which the walker can take the first two steps, and two possible directions in which the walker can take the second two steps. Therefore, there are a total of 4 possible paths that the walker can take to reach a site which is only 2 steps away.
The probability of taking any one of these paths is $(1/4)^4$, since each step has a probability of 1/4 of being taken. Therefore, the total probability of reaching a site which is only 2 steps away via Case 1 is:
$$4 \times (1/4)^4 = 1/64$$
Case 2: The walker takes one step in one direction, then turns 90 degrees and takes another step, then turns 180 degrees and takes a third step, and finally turns 90 degrees again and takes a fourth step.
In this case, there are four possible directions in which the walker can take the first step, and two possible directions in which the walker can take the second step (since it must be perpendicular to the first step). Once the first two steps have been taken, the direction of the next two steps is uniquely determined.
Therefore, there are a total of 4 x 2 = 8 possible paths that the walker can take to reach a site which is only 2 steps away via Case 2.
The probability of taking any one of these paths is $(1/4)^4$, since each step has a probability of 1/4 of being taken. Therefore, the total probability of reaching a site which is only 2 steps away via Case 2 is:
$$8 \times (1/4)^4 = 1/32$$
Final Probability: The total probability of reaching a site which is only 2 steps away is the sum of the probabilities obtained from Case 1 and Case 2:
$$1/64 + 1/32 = 3/128$$
Therefore, rounding off to two decimal places, the probability is between 0.44 and 0.48.
Approach:
To solve this problem, we can consider the possible paths that the walker can take to reach a site which is only 2 steps away.
There are two possible ways to reach a site which is only 2 steps away:
1. The walker takes two steps in one direction, and then two steps in a perpendicular direction.
2. The walker takes one step in one direction, then turns 90 degrees and takes another step, then turns 180 degrees and takes a third step, and finally turns 90 degrees again and takes a fourth step.
Let us consider each of these cases separately:
Case 1: The walker takes two steps in one direction, and then two steps in a perpendicular direction.
In this case, there are two possible directions in which the walker can take the first two steps, and two possible directions in which the walker can take the second two steps. Therefore, there are a total of 4 possible paths that the walker can take to reach a site which is only 2 steps away.
The probability of taking any one of these paths is $(1/4)^4$, since each step has a probability of 1/4 of being taken. Therefore, the total probability of reaching a site which is only 2 steps away via Case 1 is:
$$4 \times (1/4)^4 = 1/64$$
Case 2: The walker takes one step in one direction, then turns 90 degrees and takes another step, then turns 180 degrees and takes a third step, and finally turns 90 degrees again and takes a fourth step.
In this case, there are four possible directions in which the walker can take the first step, and two possible directions in which the walker can take the second step (since it must be perpendicular to the first step). Once the first two steps have been taken, the direction of the next two steps is uniquely determined.
Therefore, there are a total of 4 x 2 = 8 possible paths that the walker can take to reach a site which is only 2 steps away via Case 2.
The probability of taking any one of these paths is $(1/4)^4$, since each step has a probability of 1/4 of being taken. Therefore, the total probability of reaching a site which is only 2 steps away via Case 2 is:
$$8 \times (1/4)^4 = 1/32$$
Final Probability: The total probability of reaching a site which is only 2 steps away is the sum of the probabilities obtained from Case 1 and Case 2:
$$1/64 + 1/32 = 3/128$$
Therefore, rounding off to two decimal places, the probability is between 0.44 and 0.48.

|
Explore Courses for GATE exam
|

|
Similar GATE Doubts
Question Description
Consider a random walker on a square lattice. Walking to each neighbouring site is equally probable. Theprobability that the walker is at a site which is only 2 steps away if he takes 4 steps in total is _____ (upto 2decimal places)Correct answer is between '0.44,0.48'. Can you explain this answer? for GATE 2025 is part of GATE preparation. The Question and answers have been prepared according to the GATE exam syllabus. Information about Consider a random walker on a square lattice. Walking to each neighbouring site is equally probable. Theprobability that the walker is at a site which is only 2 steps away if he takes 4 steps in total is _____ (upto 2decimal places)Correct answer is between '0.44,0.48'. Can you explain this answer? covers all topics & solutions for GATE 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for Consider a random walker on a square lattice. Walking to each neighbouring site is equally probable. Theprobability that the walker is at a site which is only 2 steps away if he takes 4 steps in total is _____ (upto 2decimal places)Correct answer is between '0.44,0.48'. Can you explain this answer?.
Consider a random walker on a square lattice. Walking to each neighbouring site is equally probable. Theprobability that the walker is at a site which is only 2 steps away if he takes 4 steps in total is _____ (upto 2decimal places)Correct answer is between '0.44,0.48'. Can you explain this answer? for GATE 2025 is part of GATE preparation. The Question and answers have been prepared according to the GATE exam syllabus. Information about Consider a random walker on a square lattice. Walking to each neighbouring site is equally probable. Theprobability that the walker is at a site which is only 2 steps away if he takes 4 steps in total is _____ (upto 2decimal places)Correct answer is between '0.44,0.48'. Can you explain this answer? covers all topics & solutions for GATE 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for Consider a random walker on a square lattice. Walking to each neighbouring site is equally probable. Theprobability that the walker is at a site which is only 2 steps away if he takes 4 steps in total is _____ (upto 2decimal places)Correct answer is between '0.44,0.48'. Can you explain this answer?.
Solutions for Consider a random walker on a square lattice. Walking to each neighbouring site is equally probable. Theprobability that the walker is at a site which is only 2 steps away if he takes 4 steps in total is _____ (upto 2decimal places)Correct answer is between '0.44,0.48'. Can you explain this answer? in English & in Hindi are available as part of our courses for GATE.
Download more important topics, notes, lectures and mock test series for GATE Exam by signing up for free.
Here you can find the meaning of Consider a random walker on a square lattice. Walking to each neighbouring site is equally probable. Theprobability that the walker is at a site which is only 2 steps away if he takes 4 steps in total is _____ (upto 2decimal places)Correct answer is between '0.44,0.48'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
Consider a random walker on a square lattice. Walking to each neighbouring site is equally probable. Theprobability that the walker is at a site which is only 2 steps away if he takes 4 steps in total is _____ (upto 2decimal places)Correct answer is between '0.44,0.48'. Can you explain this answer?, a detailed solution for Consider a random walker on a square lattice. Walking to each neighbouring site is equally probable. Theprobability that the walker is at a site which is only 2 steps away if he takes 4 steps in total is _____ (upto 2decimal places)Correct answer is between '0.44,0.48'. Can you explain this answer? has been provided alongside types of Consider a random walker on a square lattice. Walking to each neighbouring site is equally probable. Theprobability that the walker is at a site which is only 2 steps away if he takes 4 steps in total is _____ (upto 2decimal places)Correct answer is between '0.44,0.48'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice Consider a random walker on a square lattice. Walking to each neighbouring site is equally probable. Theprobability that the walker is at a site which is only 2 steps away if he takes 4 steps in total is _____ (upto 2decimal places)Correct answer is between '0.44,0.48'. Can you explain this answer? tests, examples and also practice GATE tests.

|
Explore Courses for GATE exam
|

|
Signup to solve all Doubts
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.















