Class 12 Exam > Class 12 Questions > A 2mf capacitor c1 is charged to a voltage of...
Start Learning for Free
A 2mf capacitor c1 is charged to a voltage of 100 v and a 4mf capacitor c2 is charged to a voltage of 50 v the capacitor are then connected in parallel.what is the loss of energy in parallel connection?
Most Upvoted Answer
A 2mf capacitor c1 is charged to a voltage of 100 v and a 4mf capacito...
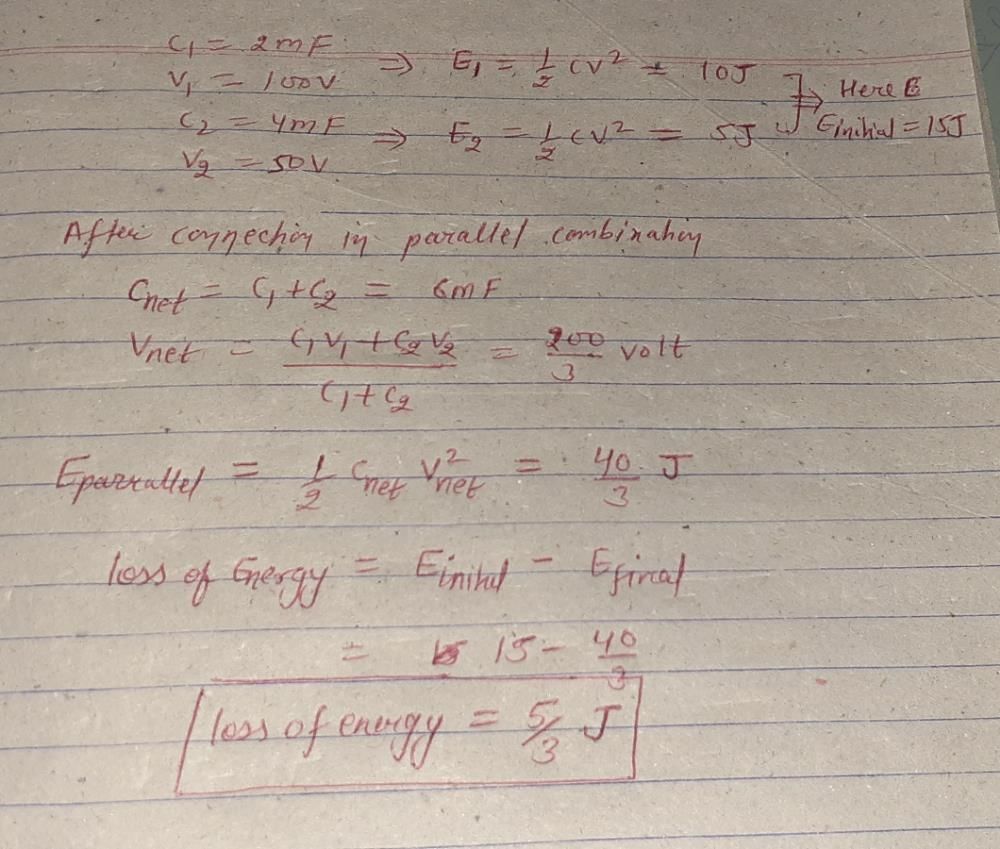
Community Answer
A 2mf capacitor c1 is charged to a voltage of 100 v and a 4mf capacito...
Introduction:
When two capacitors are connected in parallel, the total capacitance increases and the voltage across each capacitor becomes the same. In this scenario, capacitor c1 (2mf) is charged to a voltage of 100 V and capacitor c2 (4mf) is charged to a voltage of 50 V.
Calculation of total capacitance:
When capacitors are connected in parallel, the total capacitance is given by the formula:
C(total) = C1 + C2
C(total) = 2mf + 4mf
C(total) = 6mf
Therefore, the total capacitance when the two capacitors are connected in parallel is 6mf.
Calculation of total charge:
The total charge on the capacitors before they are connected in parallel is given by the formula:
Q(total) = C1 x V1 + C2 x V2
Q(total) = 2mf x 100V + 4mf x 50V
Q(total) = 200mfV + 200mfV
Q(total) = 400mfV
Therefore, the total charge on the capacitors before they are connected in parallel is 400mfV.
Calculation of final voltage:
When the capacitors are connected in parallel, the voltage across each capacitor becomes the same. Therefore, the final voltage across each capacitor is given by the formula:
V(final) = Q(total) / C(total)
V(final) = 400mfV / 6mf
V(final) = 66.67V
Therefore, the final voltage across each capacitor when they are connected in parallel is 66.67V.
Calculation of energy loss:
The energy loss in the parallel connection of capacitors is given by the formula:
E(loss) = (C1 x V1^2 + C2 x V2^2 - C(total) x V(final)^2) / 2
E(loss) = (2mf x 100V^2 + 4mf x 50V^2 - 6mf x 66.67V^2) / 2
E(loss) = (20,000mfV^2 + 10,000mfV^2 - 22,225mfV^2) / 2
E(loss) = 7,887.5mJ
Therefore, the energy loss in the parallel connection of capacitors is 7,887.5mJ.
Explanation of energy loss:
The energy loss occurs due to the conversion of electrical energy into heat energy during the charging and discharging of the capacitors. When the capacitors are charged to different voltages and then connected in parallel, the charge flows from the capacitor with higher voltage to the capacitor with lower voltage until the voltages across both capacitors become equal. During this process, energy is lost due to the internal resistance of the capacitors and the wires connecting them. This energy loss is dissipated as heat energy and cannot be recovered. Therefore, the energy loss in the parallel connection of capacitors is an important consideration in practical applications.
When two capacitors are connected in parallel, the total capacitance increases and the voltage across each capacitor becomes the same. In this scenario, capacitor c1 (2mf) is charged to a voltage of 100 V and capacitor c2 (4mf) is charged to a voltage of 50 V.
Calculation of total capacitance:
When capacitors are connected in parallel, the total capacitance is given by the formula:
C(total) = C1 + C2
C(total) = 2mf + 4mf
C(total) = 6mf
Therefore, the total capacitance when the two capacitors are connected in parallel is 6mf.
Calculation of total charge:
The total charge on the capacitors before they are connected in parallel is given by the formula:
Q(total) = C1 x V1 + C2 x V2
Q(total) = 2mf x 100V + 4mf x 50V
Q(total) = 200mfV + 200mfV
Q(total) = 400mfV
Therefore, the total charge on the capacitors before they are connected in parallel is 400mfV.
Calculation of final voltage:
When the capacitors are connected in parallel, the voltage across each capacitor becomes the same. Therefore, the final voltage across each capacitor is given by the formula:
V(final) = Q(total) / C(total)
V(final) = 400mfV / 6mf
V(final) = 66.67V
Therefore, the final voltage across each capacitor when they are connected in parallel is 66.67V.
Calculation of energy loss:
The energy loss in the parallel connection of capacitors is given by the formula:
E(loss) = (C1 x V1^2 + C2 x V2^2 - C(total) x V(final)^2) / 2
E(loss) = (2mf x 100V^2 + 4mf x 50V^2 - 6mf x 66.67V^2) / 2
E(loss) = (20,000mfV^2 + 10,000mfV^2 - 22,225mfV^2) / 2
E(loss) = 7,887.5mJ
Therefore, the energy loss in the parallel connection of capacitors is 7,887.5mJ.
Explanation of energy loss:
The energy loss occurs due to the conversion of electrical energy into heat energy during the charging and discharging of the capacitors. When the capacitors are charged to different voltages and then connected in parallel, the charge flows from the capacitor with higher voltage to the capacitor with lower voltage until the voltages across both capacitors become equal. During this process, energy is lost due to the internal resistance of the capacitors and the wires connecting them. This energy loss is dissipated as heat energy and cannot be recovered. Therefore, the energy loss in the parallel connection of capacitors is an important consideration in practical applications.

|
Explore Courses for Class 12 exam
|

|
Similar Class 12 Doubts
A 2mf capacitor c1 is charged to a voltage of 100 v and a 4mf capacitor c2 is charged to a voltage of 50 v the capacitor are then connected in parallel.what is the loss of energy in parallel connection?
Question Description
A 2mf capacitor c1 is charged to a voltage of 100 v and a 4mf capacitor c2 is charged to a voltage of 50 v the capacitor are then connected in parallel.what is the loss of energy in parallel connection? for Class 12 2024 is part of Class 12 preparation. The Question and answers have been prepared according to the Class 12 exam syllabus. Information about A 2mf capacitor c1 is charged to a voltage of 100 v and a 4mf capacitor c2 is charged to a voltage of 50 v the capacitor are then connected in parallel.what is the loss of energy in parallel connection? covers all topics & solutions for Class 12 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for A 2mf capacitor c1 is charged to a voltage of 100 v and a 4mf capacitor c2 is charged to a voltage of 50 v the capacitor are then connected in parallel.what is the loss of energy in parallel connection?.
A 2mf capacitor c1 is charged to a voltage of 100 v and a 4mf capacitor c2 is charged to a voltage of 50 v the capacitor are then connected in parallel.what is the loss of energy in parallel connection? for Class 12 2024 is part of Class 12 preparation. The Question and answers have been prepared according to the Class 12 exam syllabus. Information about A 2mf capacitor c1 is charged to a voltage of 100 v and a 4mf capacitor c2 is charged to a voltage of 50 v the capacitor are then connected in parallel.what is the loss of energy in parallel connection? covers all topics & solutions for Class 12 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for A 2mf capacitor c1 is charged to a voltage of 100 v and a 4mf capacitor c2 is charged to a voltage of 50 v the capacitor are then connected in parallel.what is the loss of energy in parallel connection?.
Solutions for A 2mf capacitor c1 is charged to a voltage of 100 v and a 4mf capacitor c2 is charged to a voltage of 50 v the capacitor are then connected in parallel.what is the loss of energy in parallel connection? in English & in Hindi are available as part of our courses for Class 12.
Download more important topics, notes, lectures and mock test series for Class 12 Exam by signing up for free.
Here you can find the meaning of A 2mf capacitor c1 is charged to a voltage of 100 v and a 4mf capacitor c2 is charged to a voltage of 50 v the capacitor are then connected in parallel.what is the loss of energy in parallel connection? defined & explained in the simplest way possible. Besides giving the explanation of
A 2mf capacitor c1 is charged to a voltage of 100 v and a 4mf capacitor c2 is charged to a voltage of 50 v the capacitor are then connected in parallel.what is the loss of energy in parallel connection?, a detailed solution for A 2mf capacitor c1 is charged to a voltage of 100 v and a 4mf capacitor c2 is charged to a voltage of 50 v the capacitor are then connected in parallel.what is the loss of energy in parallel connection? has been provided alongside types of A 2mf capacitor c1 is charged to a voltage of 100 v and a 4mf capacitor c2 is charged to a voltage of 50 v the capacitor are then connected in parallel.what is the loss of energy in parallel connection? theory, EduRev gives you an
ample number of questions to practice A 2mf capacitor c1 is charged to a voltage of 100 v and a 4mf capacitor c2 is charged to a voltage of 50 v the capacitor are then connected in parallel.what is the loss of energy in parallel connection? tests, examples and also practice Class 12 tests.

|
Explore Courses for Class 12 exam
|

|
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.



















