Computer Science Engineering (CSE) Exam > Computer Science Engineering (CSE) Questions > Let G be a weighted undirected graph and e be...
Start Learning for Free
Let G be a weighted undirected graph and e be an edge with maximum weight in G. Suppose there is a minimum weight spanning tree in G containing the edge e. Which of the following statements is always TRUE?
- a)There exists a cutset in G having all edges of maximum weight.
- b)There exists a cycle in G having all edges of maximum weight
- c)Edge e cannot be contained in a cycle.
- d)All edges in G have the same weight
Correct answer is option 'A'. Can you explain this answer?
| FREE This question is part of | Download PDF Attempt this Test |
Verified Answer
Let G be a weighted undirected graph and e be an edge with maximum wei...
Background : Given a connected and undirected graph, a spanning tree of that graph is a subgraph that is a tree and connects all the vertices together.
- A spanning tree has exactly V - 1 edges.
- A single graph can have many different spanning trees. A minimum spanning tree (MST) or minimum weight spanning tree for a weighted, connected and undirected graph is a spanning tree with weight less than or equal to the weight of every other spanning tree. The weight of a spanning tree is the sum of weights given to each edge of the spanning tree.
- There can be more that one possible spanning trees of a graph. For example, the graph in this question has 6 possible spanning trees.
- MST has lightest edge of every cutset. Remember Prim's algorithm which basically picks the lightest edge from every cutset.
Choices of this question : a) There exists a cutset in G having all edges of maximum weight : This is correct. If there is a heaviest edge in MST, then there exist a cut with all edges with weight equal to heavies edge. See point 4 discussed in above background.
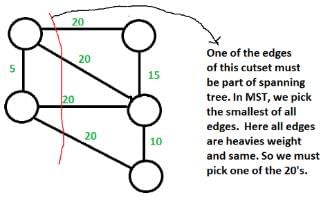
b) There exists a cycle in G having all edges of maximum weight : Not always TRUE. The cutset of heaviest edge may contain only one edge. In fact there may be overall one edge of heavies weight which is part of MST (Consider a graph with two components which are connected by only one edge and this edge is the heavies) c) Edge e cannot be contained in a cycle. Not Always True. The curset may form cycle with other edges. d) All edges in G have the same weight Not always True. As discussed in option b, there can be only one edge of heaviest weight.
Most Upvoted Answer
Let G be a weighted undirected graph and e be an edge with maximum wei...
Explanation:
To understand why option A is always true, let's consider the scenario where there is a minimum weight spanning tree (MST) containing the edge e.
1. Definition of a Cutset:
A cutset in a graph is a set of edges that, when removed, disconnects the graph into two or more components.
2. Properties of an MST:
- An MST is a connected subgraph that includes all the vertices of the original graph, with the minimum total weight.
- In an MST, there is exactly one path between any two vertices.
- An MST does not contain any cycles.
3. Proof for Option A:
- Suppose there exists a minimum weight spanning tree (MST) containing the edge e.
- If e is the edge with the maximum weight in the graph, then it must also be the edge with the maximum weight in the MST.
- Now, consider removing the edge e from the MST. This will disconnect the MST into two or more components.
- Since e is the edge with the maximum weight, the cutset that disconnects the MST will contain all the edges of maximum weight.
- Therefore, there exists a cutset in G having all edges of maximum weight.
4. Explanation for Other Options:
- Option B: There may or may not exist a cycle in G containing all edges of maximum weight. It depends on the specific graph and its weights. So, this option is not always true.
- Option C: This statement contradicts the assumption that there is a minimum weight spanning tree containing the edge e. So, this option is not always true.
- Option D: This statement is not related to the given scenario and does not provide any information about the existence of a cutset. So, this option is not always true.
Conclusion:
Based on the properties of an MST and the given assumptions, the statement in option A is always true. There will always exist a cutset in G having all edges of maximum weight.
To understand why option A is always true, let's consider the scenario where there is a minimum weight spanning tree (MST) containing the edge e.
1. Definition of a Cutset:
A cutset in a graph is a set of edges that, when removed, disconnects the graph into two or more components.
2. Properties of an MST:
- An MST is a connected subgraph that includes all the vertices of the original graph, with the minimum total weight.
- In an MST, there is exactly one path between any two vertices.
- An MST does not contain any cycles.
3. Proof for Option A:
- Suppose there exists a minimum weight spanning tree (MST) containing the edge e.
- If e is the edge with the maximum weight in the graph, then it must also be the edge with the maximum weight in the MST.
- Now, consider removing the edge e from the MST. This will disconnect the MST into two or more components.
- Since e is the edge with the maximum weight, the cutset that disconnects the MST will contain all the edges of maximum weight.
- Therefore, there exists a cutset in G having all edges of maximum weight.
4. Explanation for Other Options:
- Option B: There may or may not exist a cycle in G containing all edges of maximum weight. It depends on the specific graph and its weights. So, this option is not always true.
- Option C: This statement contradicts the assumption that there is a minimum weight spanning tree containing the edge e. So, this option is not always true.
- Option D: This statement is not related to the given scenario and does not provide any information about the existence of a cutset. So, this option is not always true.
Conclusion:
Based on the properties of an MST and the given assumptions, the statement in option A is always true. There will always exist a cutset in G having all edges of maximum weight.
Attention Computer Science Engineering (CSE) Students!
To make sure you are not studying endlessly, EduRev has designed Computer Science Engineering (CSE) study material, with Structured Courses, Videos, & Test Series. Plus get personalized analysis, doubt solving and improvement plans to achieve a great score in Computer Science Engineering (CSE).

|
Explore Courses for Computer Science Engineering (CSE) exam
|

|
Similar Computer Science Engineering (CSE) Doubts
Let G be a weighted undirected graph and e be an edge with maximum weight in G. Suppose there is a minimum weight spanning tree in G containing the edge e. Which of the following statements is always TRUE?a)There exists a cutset in G having all edges of maximum weight.b)There exists a cycle in G having all edges of maximum weightc)Edge e cannot be contained in a cycle.d)All edges in G have the same weightCorrect answer is option 'A'. Can you explain this answer?
Question Description
Let G be a weighted undirected graph and e be an edge with maximum weight in G. Suppose there is a minimum weight spanning tree in G containing the edge e. Which of the following statements is always TRUE?a)There exists a cutset in G having all edges of maximum weight.b)There exists a cycle in G having all edges of maximum weightc)Edge e cannot be contained in a cycle.d)All edges in G have the same weightCorrect answer is option 'A'. Can you explain this answer? for Computer Science Engineering (CSE) 2024 is part of Computer Science Engineering (CSE) preparation. The Question and answers have been prepared according to the Computer Science Engineering (CSE) exam syllabus. Information about Let G be a weighted undirected graph and e be an edge with maximum weight in G. Suppose there is a minimum weight spanning tree in G containing the edge e. Which of the following statements is always TRUE?a)There exists a cutset in G having all edges of maximum weight.b)There exists a cycle in G having all edges of maximum weightc)Edge e cannot be contained in a cycle.d)All edges in G have the same weightCorrect answer is option 'A'. Can you explain this answer? covers all topics & solutions for Computer Science Engineering (CSE) 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for Let G be a weighted undirected graph and e be an edge with maximum weight in G. Suppose there is a minimum weight spanning tree in G containing the edge e. Which of the following statements is always TRUE?a)There exists a cutset in G having all edges of maximum weight.b)There exists a cycle in G having all edges of maximum weightc)Edge e cannot be contained in a cycle.d)All edges in G have the same weightCorrect answer is option 'A'. Can you explain this answer?.
Let G be a weighted undirected graph and e be an edge with maximum weight in G. Suppose there is a minimum weight spanning tree in G containing the edge e. Which of the following statements is always TRUE?a)There exists a cutset in G having all edges of maximum weight.b)There exists a cycle in G having all edges of maximum weightc)Edge e cannot be contained in a cycle.d)All edges in G have the same weightCorrect answer is option 'A'. Can you explain this answer? for Computer Science Engineering (CSE) 2024 is part of Computer Science Engineering (CSE) preparation. The Question and answers have been prepared according to the Computer Science Engineering (CSE) exam syllabus. Information about Let G be a weighted undirected graph and e be an edge with maximum weight in G. Suppose there is a minimum weight spanning tree in G containing the edge e. Which of the following statements is always TRUE?a)There exists a cutset in G having all edges of maximum weight.b)There exists a cycle in G having all edges of maximum weightc)Edge e cannot be contained in a cycle.d)All edges in G have the same weightCorrect answer is option 'A'. Can you explain this answer? covers all topics & solutions for Computer Science Engineering (CSE) 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for Let G be a weighted undirected graph and e be an edge with maximum weight in G. Suppose there is a minimum weight spanning tree in G containing the edge e. Which of the following statements is always TRUE?a)There exists a cutset in G having all edges of maximum weight.b)There exists a cycle in G having all edges of maximum weightc)Edge e cannot be contained in a cycle.d)All edges in G have the same weightCorrect answer is option 'A'. Can you explain this answer?.
Solutions for Let G be a weighted undirected graph and e be an edge with maximum weight in G. Suppose there is a minimum weight spanning tree in G containing the edge e. Which of the following statements is always TRUE?a)There exists a cutset in G having all edges of maximum weight.b)There exists a cycle in G having all edges of maximum weightc)Edge e cannot be contained in a cycle.d)All edges in G have the same weightCorrect answer is option 'A'. Can you explain this answer? in English & in Hindi are available as part of our courses for Computer Science Engineering (CSE).
Download more important topics, notes, lectures and mock test series for Computer Science Engineering (CSE) Exam by signing up for free.
Here you can find the meaning of Let G be a weighted undirected graph and e be an edge with maximum weight in G. Suppose there is a minimum weight spanning tree in G containing the edge e. Which of the following statements is always TRUE?a)There exists a cutset in G having all edges of maximum weight.b)There exists a cycle in G having all edges of maximum weightc)Edge e cannot be contained in a cycle.d)All edges in G have the same weightCorrect answer is option 'A'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
Let G be a weighted undirected graph and e be an edge with maximum weight in G. Suppose there is a minimum weight spanning tree in G containing the edge e. Which of the following statements is always TRUE?a)There exists a cutset in G having all edges of maximum weight.b)There exists a cycle in G having all edges of maximum weightc)Edge e cannot be contained in a cycle.d)All edges in G have the same weightCorrect answer is option 'A'. Can you explain this answer?, a detailed solution for Let G be a weighted undirected graph and e be an edge with maximum weight in G. Suppose there is a minimum weight spanning tree in G containing the edge e. Which of the following statements is always TRUE?a)There exists a cutset in G having all edges of maximum weight.b)There exists a cycle in G having all edges of maximum weightc)Edge e cannot be contained in a cycle.d)All edges in G have the same weightCorrect answer is option 'A'. Can you explain this answer? has been provided alongside types of Let G be a weighted undirected graph and e be an edge with maximum weight in G. Suppose there is a minimum weight spanning tree in G containing the edge e. Which of the following statements is always TRUE?a)There exists a cutset in G having all edges of maximum weight.b)There exists a cycle in G having all edges of maximum weightc)Edge e cannot be contained in a cycle.d)All edges in G have the same weightCorrect answer is option 'A'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice Let G be a weighted undirected graph and e be an edge with maximum weight in G. Suppose there is a minimum weight spanning tree in G containing the edge e. Which of the following statements is always TRUE?a)There exists a cutset in G having all edges of maximum weight.b)There exists a cycle in G having all edges of maximum weightc)Edge e cannot be contained in a cycle.d)All edges in G have the same weightCorrect answer is option 'A'. Can you explain this answer? tests, examples and also practice Computer Science Engineering (CSE) tests.

|
Explore Courses for Computer Science Engineering (CSE) exam
|

|
Suggested Free Tests
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.
























