Physics Exam > Physics Questions > Two identical sonometer wires have a fundamen...
Start Learning for Free
Two identical sonometer wires have a fundamental frequency of 500 vibrations per second when kept under the same tension. The fractional increase in the tension of the one wire that would cause an occurrence of 5 beats/sec. When both wires vibrate together is ______.
Correct answer is '0.02'. Can you explain this answer?
Most Upvoted Answer
Two identical sonometer wires have a fundamental frequency of 500 vibr...
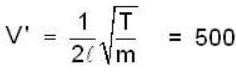
let the tension of one wire be increased by ΔT
The new frequency V’ is V’ =
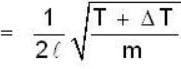
Dividing by eqn (2) by eq (1) :-
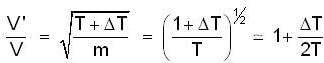
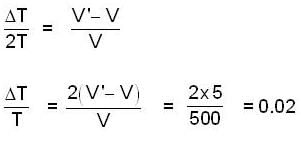
Free Test
FREE
| Start Free Test |
Community Answer
Two identical sonometer wires have a fundamental frequency of 500 vibr...
Given information:
- Two identical sonometer wires have a fundamental frequency of 500 vibrations per second when kept under the same tension.
To find:
- The fractional increase in the tension of the one wire that would cause an occurrence of 5 beats/sec when both wires vibrate together.
Let's break down the problem step by step:
1. Understanding beats:
- When two sound waves of slightly different frequencies are superimposed, they produce a phenomenon known as beats.
- Beats are periodic variations in the loudness or intensity of sound when two waves interfere constructively and destructively.
- The number of beats produced per second is equal to the difference in frequency between the two waves.
2. Relationship between frequency and tension:
- In the case of a stretched wire, the frequency of vibration is directly proportional to the square root of tension.
- Mathematically, f ∝ √T, where f is the frequency and T is the tension.
3. Finding the frequency difference:
- The two wires have a fundamental frequency of 500 vibrations per second when kept under the same tension.
- Therefore, the frequency of each wire is 500 Hz.
- For beats to occur, the frequency of one wire needs to be slightly different from the other.
- Let's assume the frequency of the second wire is (500 + Δf) Hz, where Δf is the frequency difference that causes 5 beats/sec.
4. Calculating the tension difference:
- From the relationship f ∝ √T, we can write the equation as f = k√T, where k is a constant.
- For the first wire: 500 = k√T1
- For the second wire: (500 + Δf) = k√T2
5. Finding the tension difference:
- Taking the ratio of the two equations: (500 + Δf)/500 = √(T2/T1)
- Squaring both sides: ((500 + Δf)/500)^2 = T2/T1
- Since the wires are identical, T2/T1 = 1
- Simplifying the equation: ((500 + Δf)/500)^2 = 1
- Solving for Δf: Δf = 500(√2 - 1) ≈ 207.11 Hz
6. Calculating the fractional increase in tension:
- Now, we need to find the fractional increase in tension that causes Δf = 207.11 Hz.
- Let's assume the tension of the first wire is T, and the tension of the second wire is T + ΔT.
- From the relationship f ∝ √T, we can write the equation as f = k√(T + ΔT)
- For the first wire: 500 = k√T
- For the second wire: (500 + Δf) = k√(T + ΔT)
7. Simplifying the equation:
- Taking the ratio of the two equations: (500 + Δf)/500 = √((T + ΔT)/T)
- Squaring both sides: ((500 + Δf)/500)^2 = (T + ΔT)/T
- Rearranging the equation: ΔT = T(((500 + Δf)/500)^2 - 1)
8. Calculating the fractional increase in tension:
- Substituting the values: ΔT = T(((500
- Two identical sonometer wires have a fundamental frequency of 500 vibrations per second when kept under the same tension.
To find:
- The fractional increase in the tension of the one wire that would cause an occurrence of 5 beats/sec when both wires vibrate together.
Let's break down the problem step by step:
1. Understanding beats:
- When two sound waves of slightly different frequencies are superimposed, they produce a phenomenon known as beats.
- Beats are periodic variations in the loudness or intensity of sound when two waves interfere constructively and destructively.
- The number of beats produced per second is equal to the difference in frequency between the two waves.
2. Relationship between frequency and tension:
- In the case of a stretched wire, the frequency of vibration is directly proportional to the square root of tension.
- Mathematically, f ∝ √T, where f is the frequency and T is the tension.
3. Finding the frequency difference:
- The two wires have a fundamental frequency of 500 vibrations per second when kept under the same tension.
- Therefore, the frequency of each wire is 500 Hz.
- For beats to occur, the frequency of one wire needs to be slightly different from the other.
- Let's assume the frequency of the second wire is (500 + Δf) Hz, where Δf is the frequency difference that causes 5 beats/sec.
4. Calculating the tension difference:
- From the relationship f ∝ √T, we can write the equation as f = k√T, where k is a constant.
- For the first wire: 500 = k√T1
- For the second wire: (500 + Δf) = k√T2
5. Finding the tension difference:
- Taking the ratio of the two equations: (500 + Δf)/500 = √(T2/T1)
- Squaring both sides: ((500 + Δf)/500)^2 = T2/T1
- Since the wires are identical, T2/T1 = 1
- Simplifying the equation: ((500 + Δf)/500)^2 = 1
- Solving for Δf: Δf = 500(√2 - 1) ≈ 207.11 Hz
6. Calculating the fractional increase in tension:
- Now, we need to find the fractional increase in tension that causes Δf = 207.11 Hz.
- Let's assume the tension of the first wire is T, and the tension of the second wire is T + ΔT.
- From the relationship f ∝ √T, we can write the equation as f = k√(T + ΔT)
- For the first wire: 500 = k√T
- For the second wire: (500 + Δf) = k√(T + ΔT)
7. Simplifying the equation:
- Taking the ratio of the two equations: (500 + Δf)/500 = √((T + ΔT)/T)
- Squaring both sides: ((500 + Δf)/500)^2 = (T + ΔT)/T
- Rearranging the equation: ΔT = T(((500 + Δf)/500)^2 - 1)
8. Calculating the fractional increase in tension:
- Substituting the values: ΔT = T(((500

|
Explore Courses for Physics exam
|

|
Similar Physics Doubts
Question Description
Two identical sonometer wires have a fundamental frequency of 500 vibrationsper second when kept under the same tension. The fractional increase in thetension of the one wire that would cause an occurrence of 5 beats/sec. Whenboth wires vibrate together is ______.Correct answer is '0.02'. Can you explain this answer? for Physics 2025 is part of Physics preparation. The Question and answers have been prepared according to the Physics exam syllabus. Information about Two identical sonometer wires have a fundamental frequency of 500 vibrationsper second when kept under the same tension. The fractional increase in thetension of the one wire that would cause an occurrence of 5 beats/sec. Whenboth wires vibrate together is ______.Correct answer is '0.02'. Can you explain this answer? covers all topics & solutions for Physics 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for Two identical sonometer wires have a fundamental frequency of 500 vibrationsper second when kept under the same tension. The fractional increase in thetension of the one wire that would cause an occurrence of 5 beats/sec. Whenboth wires vibrate together is ______.Correct answer is '0.02'. Can you explain this answer?.
Two identical sonometer wires have a fundamental frequency of 500 vibrationsper second when kept under the same tension. The fractional increase in thetension of the one wire that would cause an occurrence of 5 beats/sec. Whenboth wires vibrate together is ______.Correct answer is '0.02'. Can you explain this answer? for Physics 2025 is part of Physics preparation. The Question and answers have been prepared according to the Physics exam syllabus. Information about Two identical sonometer wires have a fundamental frequency of 500 vibrationsper second when kept under the same tension. The fractional increase in thetension of the one wire that would cause an occurrence of 5 beats/sec. Whenboth wires vibrate together is ______.Correct answer is '0.02'. Can you explain this answer? covers all topics & solutions for Physics 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for Two identical sonometer wires have a fundamental frequency of 500 vibrationsper second when kept under the same tension. The fractional increase in thetension of the one wire that would cause an occurrence of 5 beats/sec. Whenboth wires vibrate together is ______.Correct answer is '0.02'. Can you explain this answer?.
Solutions for Two identical sonometer wires have a fundamental frequency of 500 vibrationsper second when kept under the same tension. The fractional increase in thetension of the one wire that would cause an occurrence of 5 beats/sec. Whenboth wires vibrate together is ______.Correct answer is '0.02'. Can you explain this answer? in English & in Hindi are available as part of our courses for Physics.
Download more important topics, notes, lectures and mock test series for Physics Exam by signing up for free.
Here you can find the meaning of Two identical sonometer wires have a fundamental frequency of 500 vibrationsper second when kept under the same tension. The fractional increase in thetension of the one wire that would cause an occurrence of 5 beats/sec. Whenboth wires vibrate together is ______.Correct answer is '0.02'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
Two identical sonometer wires have a fundamental frequency of 500 vibrationsper second when kept under the same tension. The fractional increase in thetension of the one wire that would cause an occurrence of 5 beats/sec. Whenboth wires vibrate together is ______.Correct answer is '0.02'. Can you explain this answer?, a detailed solution for Two identical sonometer wires have a fundamental frequency of 500 vibrationsper second when kept under the same tension. The fractional increase in thetension of the one wire that would cause an occurrence of 5 beats/sec. Whenboth wires vibrate together is ______.Correct answer is '0.02'. Can you explain this answer? has been provided alongside types of Two identical sonometer wires have a fundamental frequency of 500 vibrationsper second when kept under the same tension. The fractional increase in thetension of the one wire that would cause an occurrence of 5 beats/sec. Whenboth wires vibrate together is ______.Correct answer is '0.02'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice Two identical sonometer wires have a fundamental frequency of 500 vibrationsper second when kept under the same tension. The fractional increase in thetension of the one wire that would cause an occurrence of 5 beats/sec. Whenboth wires vibrate together is ______.Correct answer is '0.02'. Can you explain this answer? tests, examples and also practice Physics tests.

|
Explore Courses for Physics exam
|

|
Signup to solve all Doubts
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.





















