JEE Exam > JEE Questions > If the pair of lines ax2 + 2 (a + b)xy + by 2...
Start Learning for Free
If the pair of lines ax2 + 2 (a + b)xy + by 2 = 0 lie along diameters of a circle and divide the circle into four sectors such that the area of one of the sectors is thrice the area of another sector then [2005]
- a)3a2 - 10ab + 3b2 = 0
- b)3a2 - 2ab + 3b2 = 0
- c)3a2 + 10ab + 3b2 = 0
- d)3a2 + 2ab+ 3b2 = 0
Correct answer is option 'D'. Can you explain this answer?
Verified Answer
If the pair of lines ax2 + 2 (a + b)xy + by 2 = 0 lie along diameters ...

As per question area of one sector = 3 area of another sector
⇒ angle at centre by one sector = 3x angle at centre by another sector
Let one angle be θ then other = 3θ
Clearly θ + 3θ = 180 ⇒ θ = 45o
⇒ angle at centre by one sector = 3x angle at centre by another sector
Let one angle be θ then other = 3θ
Clearly θ + 3θ = 180 ⇒ θ = 45o
∴ Angle between the diameters represented by combined equation
ax2 + 2 ( a + b ) xy + by2 = 0 is 45o
∴ Using 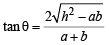
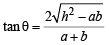
we get 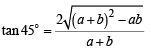
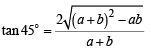

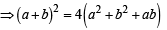
⇒ a2 + b2 + 2ab = 4a2 + 4b2 +4ab ⇒ 3a2 + 3b2 + 2ab = 0
Most Upvoted Answer
If the pair of lines ax2 + 2 (a + b)xy + by 2 = 0 lie along diameters ...
Understanding the Problem
The problem involves a pair of lines represented by the equation ax^2 + 2(a + b)xy + by^2 = 0. These lines are diameters of a circle, dividing it into four sectors. The key condition is that the area of one sector is three times that of another.
Conditions for Diameters
- For the lines to be diameters, their slopes must be negative reciprocals.
- The angle between the two lines must be 90 degrees, ensuring they meet at the center of the circle.
Area Relationship
- Let the areas of the sectors be A and 3A.
- The total area of the circle is divided into four sectors, so we have A + 3A = Area of Circle = πr².
- From this, we derive that the total area (4A) implies that A must be πr²/4.
Finding the Condition
To find the condition on a and b, we analyze the quadratic equation and apply the relationship derived from the slopes of the diameters.
- The discriminant of the quadratic must be non-negative.
- We need to establish the relationship based on the given area ratio.
Conclusion: The Correct Condition
Upon solving the equations and substituting the conditions, we arrive at:
- 3a² + 2ab + 3b² = 0
Thus, the correct answer is option 'D'.
This relationship ensures that the areas of the sectors maintain the specified ratio, satisfying the problem's requirements.
The problem involves a pair of lines represented by the equation ax^2 + 2(a + b)xy + by^2 = 0. These lines are diameters of a circle, dividing it into four sectors. The key condition is that the area of one sector is three times that of another.
Conditions for Diameters
- For the lines to be diameters, their slopes must be negative reciprocals.
- The angle between the two lines must be 90 degrees, ensuring they meet at the center of the circle.
Area Relationship
- Let the areas of the sectors be A and 3A.
- The total area of the circle is divided into four sectors, so we have A + 3A = Area of Circle = πr².
- From this, we derive that the total area (4A) implies that A must be πr²/4.
Finding the Condition
To find the condition on a and b, we analyze the quadratic equation and apply the relationship derived from the slopes of the diameters.
- The discriminant of the quadratic must be non-negative.
- We need to establish the relationship based on the given area ratio.
Conclusion: The Correct Condition
Upon solving the equations and substituting the conditions, we arrive at:
- 3a² + 2ab + 3b² = 0
Thus, the correct answer is option 'D'.
This relationship ensures that the areas of the sectors maintain the specified ratio, satisfying the problem's requirements.

|
Explore Courses for JEE exam
|

|
Question Description
If the pair of lines ax2 + 2 (a + b)xy + by 2 = 0 lie along diameters of a circle and divide the circle into four sectors such that the area of one of the sectors is thrice the area of another sector then [2005]a)3a2 - 10ab + 3b2 =0b)3a2 - 2ab + 3b2= 0c)3a2 + 10ab + 3b2= 0d)3a2 + 2ab+ 3b2 = 0Correct answer is option 'D'. Can you explain this answer? for JEE 2025 is part of JEE preparation. The Question and answers have been prepared according to the JEE exam syllabus. Information about If the pair of lines ax2 + 2 (a + b)xy + by 2 = 0 lie along diameters of a circle and divide the circle into four sectors such that the area of one of the sectors is thrice the area of another sector then [2005]a)3a2 - 10ab + 3b2 =0b)3a2 - 2ab + 3b2= 0c)3a2 + 10ab + 3b2= 0d)3a2 + 2ab+ 3b2 = 0Correct answer is option 'D'. Can you explain this answer? covers all topics & solutions for JEE 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for If the pair of lines ax2 + 2 (a + b)xy + by 2 = 0 lie along diameters of a circle and divide the circle into four sectors such that the area of one of the sectors is thrice the area of another sector then [2005]a)3a2 - 10ab + 3b2 =0b)3a2 - 2ab + 3b2= 0c)3a2 + 10ab + 3b2= 0d)3a2 + 2ab+ 3b2 = 0Correct answer is option 'D'. Can you explain this answer?.
If the pair of lines ax2 + 2 (a + b)xy + by 2 = 0 lie along diameters of a circle and divide the circle into four sectors such that the area of one of the sectors is thrice the area of another sector then [2005]a)3a2 - 10ab + 3b2 =0b)3a2 - 2ab + 3b2= 0c)3a2 + 10ab + 3b2= 0d)3a2 + 2ab+ 3b2 = 0Correct answer is option 'D'. Can you explain this answer? for JEE 2025 is part of JEE preparation. The Question and answers have been prepared according to the JEE exam syllabus. Information about If the pair of lines ax2 + 2 (a + b)xy + by 2 = 0 lie along diameters of a circle and divide the circle into four sectors such that the area of one of the sectors is thrice the area of another sector then [2005]a)3a2 - 10ab + 3b2 =0b)3a2 - 2ab + 3b2= 0c)3a2 + 10ab + 3b2= 0d)3a2 + 2ab+ 3b2 = 0Correct answer is option 'D'. Can you explain this answer? covers all topics & solutions for JEE 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for If the pair of lines ax2 + 2 (a + b)xy + by 2 = 0 lie along diameters of a circle and divide the circle into four sectors such that the area of one of the sectors is thrice the area of another sector then [2005]a)3a2 - 10ab + 3b2 =0b)3a2 - 2ab + 3b2= 0c)3a2 + 10ab + 3b2= 0d)3a2 + 2ab+ 3b2 = 0Correct answer is option 'D'. Can you explain this answer?.
Solutions for If the pair of lines ax2 + 2 (a + b)xy + by 2 = 0 lie along diameters of a circle and divide the circle into four sectors such that the area of one of the sectors is thrice the area of another sector then [2005]a)3a2 - 10ab + 3b2 =0b)3a2 - 2ab + 3b2= 0c)3a2 + 10ab + 3b2= 0d)3a2 + 2ab+ 3b2 = 0Correct answer is option 'D'. Can you explain this answer? in English & in Hindi are available as part of our courses for JEE.
Download more important topics, notes, lectures and mock test series for JEE Exam by signing up for free.
Here you can find the meaning of If the pair of lines ax2 + 2 (a + b)xy + by 2 = 0 lie along diameters of a circle and divide the circle into four sectors such that the area of one of the sectors is thrice the area of another sector then [2005]a)3a2 - 10ab + 3b2 =0b)3a2 - 2ab + 3b2= 0c)3a2 + 10ab + 3b2= 0d)3a2 + 2ab+ 3b2 = 0Correct answer is option 'D'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
If the pair of lines ax2 + 2 (a + b)xy + by 2 = 0 lie along diameters of a circle and divide the circle into four sectors such that the area of one of the sectors is thrice the area of another sector then [2005]a)3a2 - 10ab + 3b2 =0b)3a2 - 2ab + 3b2= 0c)3a2 + 10ab + 3b2= 0d)3a2 + 2ab+ 3b2 = 0Correct answer is option 'D'. Can you explain this answer?, a detailed solution for If the pair of lines ax2 + 2 (a + b)xy + by 2 = 0 lie along diameters of a circle and divide the circle into four sectors such that the area of one of the sectors is thrice the area of another sector then [2005]a)3a2 - 10ab + 3b2 =0b)3a2 - 2ab + 3b2= 0c)3a2 + 10ab + 3b2= 0d)3a2 + 2ab+ 3b2 = 0Correct answer is option 'D'. Can you explain this answer? has been provided alongside types of If the pair of lines ax2 + 2 (a + b)xy + by 2 = 0 lie along diameters of a circle and divide the circle into four sectors such that the area of one of the sectors is thrice the area of another sector then [2005]a)3a2 - 10ab + 3b2 =0b)3a2 - 2ab + 3b2= 0c)3a2 + 10ab + 3b2= 0d)3a2 + 2ab+ 3b2 = 0Correct answer is option 'D'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice If the pair of lines ax2 + 2 (a + b)xy + by 2 = 0 lie along diameters of a circle and divide the circle into four sectors such that the area of one of the sectors is thrice the area of another sector then [2005]a)3a2 - 10ab + 3b2 =0b)3a2 - 2ab + 3b2= 0c)3a2 + 10ab + 3b2= 0d)3a2 + 2ab+ 3b2 = 0Correct answer is option 'D'. Can you explain this answer? tests, examples and also practice JEE tests.

|
Explore Courses for JEE exam
|

|
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.


















