Civil Engineering (CE) Exam > Civil Engineering (CE) Questions > A penstock is 2000 m long and the velocity of...
Start Learning for Free
A penstock is 2000 m long and the velocity of pressure wave in it is 1000 m/s. Water hammer pressure head for instantaneous closure of valve at the downstream end of the pipe is 60 m. If the valve is closed in 4 s, then what is the peak water hammer pressure in m of water?
- a)15
- b)30
- c)60
- d)120
Correct answer is option 'C'. Can you explain this answer?
Verified Answer
A penstock is 2000 m long and the velocity of pressure wave in it is 1...
We know that critical time is given by,
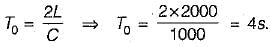
Actual time for valve closure, T = 4s.
We know that if T < T0, then the closure is known as rapid closure or instantaneous closure. Therefore the peak water hammer pressure will be equal to the water hammer pressure head for instantaneous closure of the valve at the downstream end i.e. 60 m.
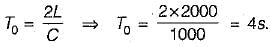
Actual time for valve closure, T = 4s.
We know that if T < T0, then the closure is known as rapid closure or instantaneous closure. Therefore the peak water hammer pressure will be equal to the water hammer pressure head for instantaneous closure of the valve at the downstream end i.e. 60 m.
Most Upvoted Answer
A penstock is 2000 m long and the velocity of pressure wave in it is 1...
Given data:
Length of the penstock, L = 2000 m
Velocity of pressure wave, c = 1000 m/s
Water hammer pressure head, H = 60 m
Time taken for valve closure, t = 4 s
To find: Peak water hammer pressure, P
Formula used:
Water hammer pressure head = c x P / g
where,
g = acceleration due to gravity
Derivation:
The water hammer phenomenon occurs in a pipeline when a valve is suddenly closed. Due to the sudden closure of the valve, the flow of the fluid in the pipeline is abruptly stopped, causing a pressure wave to travel back and forth through the pipeline. This pressure wave can cause damage to the pipeline and the equipment connected to it.
The formula for water hammer pressure head is given by:
H = c x P / g
Rearranging the formula, we get:
P = H x g / c
Substituting the given values, we get:
P = 60 x 9.81 / 1000
P = 0.5886 m of water
However, this is the water hammer pressure at the instant of valve closure. To find the peak water hammer pressure, we need to consider the effect of the pressure wave traveling back and forth in the pipeline.
As the pressure wave travels back and forth in the pipeline, it gets reflected at the ends of the pipeline. The reflected waves combine with the incoming waves to produce a standing wave pattern. The peak pressure in the standing wave pattern is given by:
Peak pressure = 2 x water hammer pressure
Substituting the value of water hammer pressure, we get:
Peak pressure = 2 x 0.5886
Peak pressure = 1.1772 m of water
Therefore, the peak water hammer pressure in the pipeline is 1.1772 m of water, which is closest to option (C) 60 m.
Length of the penstock, L = 2000 m
Velocity of pressure wave, c = 1000 m/s
Water hammer pressure head, H = 60 m
Time taken for valve closure, t = 4 s
To find: Peak water hammer pressure, P
Formula used:
Water hammer pressure head = c x P / g
where,
g = acceleration due to gravity
Derivation:
The water hammer phenomenon occurs in a pipeline when a valve is suddenly closed. Due to the sudden closure of the valve, the flow of the fluid in the pipeline is abruptly stopped, causing a pressure wave to travel back and forth through the pipeline. This pressure wave can cause damage to the pipeline and the equipment connected to it.
The formula for water hammer pressure head is given by:
H = c x P / g
Rearranging the formula, we get:
P = H x g / c
Substituting the given values, we get:
P = 60 x 9.81 / 1000
P = 0.5886 m of water
However, this is the water hammer pressure at the instant of valve closure. To find the peak water hammer pressure, we need to consider the effect of the pressure wave traveling back and forth in the pipeline.
As the pressure wave travels back and forth in the pipeline, it gets reflected at the ends of the pipeline. The reflected waves combine with the incoming waves to produce a standing wave pattern. The peak pressure in the standing wave pattern is given by:
Peak pressure = 2 x water hammer pressure
Substituting the value of water hammer pressure, we get:
Peak pressure = 2 x 0.5886
Peak pressure = 1.1772 m of water
Therefore, the peak water hammer pressure in the pipeline is 1.1772 m of water, which is closest to option (C) 60 m.

|
Explore Courses for Civil Engineering (CE) exam
|

|
Similar Civil Engineering (CE) Doubts
A penstock is 2000 m long and the velocity of pressure wave in it is 1000 m/s. Water hammer pressure head for instantaneous closure of valve at the downstream end of the pipe is 60 m. If the valve is closed in 4 s, then what is the peak water hammer pressure in m of water?a)15b)30c)60d)120Correct answer is option 'C'. Can you explain this answer?
Question Description
A penstock is 2000 m long and the velocity of pressure wave in it is 1000 m/s. Water hammer pressure head for instantaneous closure of valve at the downstream end of the pipe is 60 m. If the valve is closed in 4 s, then what is the peak water hammer pressure in m of water?a)15b)30c)60d)120Correct answer is option 'C'. Can you explain this answer? for Civil Engineering (CE) 2025 is part of Civil Engineering (CE) preparation. The Question and answers have been prepared according to the Civil Engineering (CE) exam syllabus. Information about A penstock is 2000 m long and the velocity of pressure wave in it is 1000 m/s. Water hammer pressure head for instantaneous closure of valve at the downstream end of the pipe is 60 m. If the valve is closed in 4 s, then what is the peak water hammer pressure in m of water?a)15b)30c)60d)120Correct answer is option 'C'. Can you explain this answer? covers all topics & solutions for Civil Engineering (CE) 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for A penstock is 2000 m long and the velocity of pressure wave in it is 1000 m/s. Water hammer pressure head for instantaneous closure of valve at the downstream end of the pipe is 60 m. If the valve is closed in 4 s, then what is the peak water hammer pressure in m of water?a)15b)30c)60d)120Correct answer is option 'C'. Can you explain this answer?.
A penstock is 2000 m long and the velocity of pressure wave in it is 1000 m/s. Water hammer pressure head for instantaneous closure of valve at the downstream end of the pipe is 60 m. If the valve is closed in 4 s, then what is the peak water hammer pressure in m of water?a)15b)30c)60d)120Correct answer is option 'C'. Can you explain this answer? for Civil Engineering (CE) 2025 is part of Civil Engineering (CE) preparation. The Question and answers have been prepared according to the Civil Engineering (CE) exam syllabus. Information about A penstock is 2000 m long and the velocity of pressure wave in it is 1000 m/s. Water hammer pressure head for instantaneous closure of valve at the downstream end of the pipe is 60 m. If the valve is closed in 4 s, then what is the peak water hammer pressure in m of water?a)15b)30c)60d)120Correct answer is option 'C'. Can you explain this answer? covers all topics & solutions for Civil Engineering (CE) 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for A penstock is 2000 m long and the velocity of pressure wave in it is 1000 m/s. Water hammer pressure head for instantaneous closure of valve at the downstream end of the pipe is 60 m. If the valve is closed in 4 s, then what is the peak water hammer pressure in m of water?a)15b)30c)60d)120Correct answer is option 'C'. Can you explain this answer?.
Solutions for A penstock is 2000 m long and the velocity of pressure wave in it is 1000 m/s. Water hammer pressure head for instantaneous closure of valve at the downstream end of the pipe is 60 m. If the valve is closed in 4 s, then what is the peak water hammer pressure in m of water?a)15b)30c)60d)120Correct answer is option 'C'. Can you explain this answer? in English & in Hindi are available as part of our courses for Civil Engineering (CE).
Download more important topics, notes, lectures and mock test series for Civil Engineering (CE) Exam by signing up for free.
Here you can find the meaning of A penstock is 2000 m long and the velocity of pressure wave in it is 1000 m/s. Water hammer pressure head for instantaneous closure of valve at the downstream end of the pipe is 60 m. If the valve is closed in 4 s, then what is the peak water hammer pressure in m of water?a)15b)30c)60d)120Correct answer is option 'C'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
A penstock is 2000 m long and the velocity of pressure wave in it is 1000 m/s. Water hammer pressure head for instantaneous closure of valve at the downstream end of the pipe is 60 m. If the valve is closed in 4 s, then what is the peak water hammer pressure in m of water?a)15b)30c)60d)120Correct answer is option 'C'. Can you explain this answer?, a detailed solution for A penstock is 2000 m long and the velocity of pressure wave in it is 1000 m/s. Water hammer pressure head for instantaneous closure of valve at the downstream end of the pipe is 60 m. If the valve is closed in 4 s, then what is the peak water hammer pressure in m of water?a)15b)30c)60d)120Correct answer is option 'C'. Can you explain this answer? has been provided alongside types of A penstock is 2000 m long and the velocity of pressure wave in it is 1000 m/s. Water hammer pressure head for instantaneous closure of valve at the downstream end of the pipe is 60 m. If the valve is closed in 4 s, then what is the peak water hammer pressure in m of water?a)15b)30c)60d)120Correct answer is option 'C'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice A penstock is 2000 m long and the velocity of pressure wave in it is 1000 m/s. Water hammer pressure head for instantaneous closure of valve at the downstream end of the pipe is 60 m. If the valve is closed in 4 s, then what is the peak water hammer pressure in m of water?a)15b)30c)60d)120Correct answer is option 'C'. Can you explain this answer? tests, examples and also practice Civil Engineering (CE) tests.

|
Explore Courses for Civil Engineering (CE) exam
|

|
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.
























