JEE Exam > JEE Questions > Let M be a 2 × 2 symmetric matrix with ...
Start Learning for Free
Let M be a 2 × 2 symmetric matrix with integer entries. Then M is invertible if
- a)The first column of M is the transpose of the second row of M
- b)The second row of M is the transpose of the first column of M
- c)M is a diagonal matrix with non-zero entries in the main diagonal
- d)The product of entries in the main diagonal of M is not the square of an integer
Correct answer is option 'C,D'. Can you explain this answer?
| FREE This question is part of | Download PDF Attempt this Test |
Verified Answer
Let M be a 2 × 2 symmetric matrix with integer entries. Then M i...
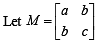where a, b, c are integers.M is invertible if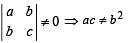 
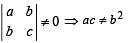
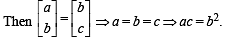
∴ (a) is not correct.
If [bc] = [ab] ⇒ b = a = c ⇒ ac = b2
∴ (b) is not correct.
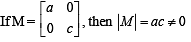
∴ M is invertible.
(c) is correct
As ac ≠ (integer)2 ⇒ ac ≠ b2
∴ (d) is correct.
(c) is correct
As ac ≠ (integer)2 ⇒ ac ≠ b2
∴ (d) is correct.
Most Upvoted Answer
Let M be a 2 × 2 symmetric matrix with integer entries. Then M i...
X 3 matrix and N be a 3 x 2 matrix. We can find their product MN as follows:
MN = ⎡⎣⎢⎢∑k=1^3 m1,kn_k,1∑k=1^3 m1,kn_k,2∑k=1^3 m1,kn_k,3∑k=1^3 m2,kn_k,1∑k=1^3 m2,kn_k,2∑k=1^3 m2,kn_k,3⎤⎦⎥⎥
where m1,k and m2,k are the entries of M and n_k,1 and n_k,2 are the entries of N.
We can simplify this expression by using matrix multiplication rules:
MN = ⎡⎣⎢⎢∑k=1^3 m1,kn_k,1∑k=1^3 m1,kn_k,2∑k=1^3 m1,kn_k,3∑k=1^3 m2,kn_k,1∑k=1^3 m2,kn_k,2∑k=1^3 m2,kn_k,3⎤⎦⎥⎥
= ⎡⎣⎢⎢m1,1n_1,1 + m1,2n_2,1 + m1,3n_3,1 m1,1n_1,2 + m1,2n_2,2 + m1,3n_3,2 m1,1n_1,3 + m1,2n_2,3 + m1,3n_3,3 m2,1n_1,1 + m2,2n_2,1 + m2,3n_3,1 m2,1n_1,2 + m2,2n_2,2 + m2,3n_3,2 m2,1n_1,3 + m2,2n_2,3 + m2,3n_3,3⎤⎦⎥⎥
Therefore, the product MN is a 2 x 2 matrix.
MN = ⎡⎣⎢⎢∑k=1^3 m1,kn_k,1∑k=1^3 m1,kn_k,2∑k=1^3 m1,kn_k,3∑k=1^3 m2,kn_k,1∑k=1^3 m2,kn_k,2∑k=1^3 m2,kn_k,3⎤⎦⎥⎥
where m1,k and m2,k are the entries of M and n_k,1 and n_k,2 are the entries of N.
We can simplify this expression by using matrix multiplication rules:
MN = ⎡⎣⎢⎢∑k=1^3 m1,kn_k,1∑k=1^3 m1,kn_k,2∑k=1^3 m1,kn_k,3∑k=1^3 m2,kn_k,1∑k=1^3 m2,kn_k,2∑k=1^3 m2,kn_k,3⎤⎦⎥⎥
= ⎡⎣⎢⎢m1,1n_1,1 + m1,2n_2,1 + m1,3n_3,1 m1,1n_1,2 + m1,2n_2,2 + m1,3n_3,2 m1,1n_1,3 + m1,2n_2,3 + m1,3n_3,3 m2,1n_1,1 + m2,2n_2,1 + m2,3n_3,1 m2,1n_1,2 + m2,2n_2,2 + m2,3n_3,2 m2,1n_1,3 + m2,2n_2,3 + m2,3n_3,3⎤⎦⎥⎥
Therefore, the product MN is a 2 x 2 matrix.
Attention JEE Students!
To make sure you are not studying endlessly, EduRev has designed JEE study material, with Structured Courses, Videos, & Test Series. Plus get personalized analysis, doubt solving and improvement plans to achieve a great score in JEE.
|
Explore Courses for JEE exam
|
|
Similar JEE Doubts
Top Courses for JEEView all
Let M be a 2 × 2 symmetric matrix with integer entries. Then M is invertible ifa)The first column of M is the transpose of the second row of Mb)The second row of M is the transpose of the first column of Mc)M is a diagonal matrix with non-zero entries in the main diagonald)The product of entries in the main diagonal of M is not the square of an integerCorrect answer is option 'C,D'. Can you explain this answer?
Question Description
Let M be a 2 × 2 symmetric matrix with integer entries. Then M is invertible ifa)The first column of M is the transpose of the second row of Mb)The second row of M is the transpose of the first column of Mc)M is a diagonal matrix with non-zero entries in the main diagonald)The product of entries in the main diagonal of M is not the square of an integerCorrect answer is option 'C,D'. Can you explain this answer? for JEE 2024 is part of JEE preparation. The Question and answers have been prepared according to the JEE exam syllabus. Information about Let M be a 2 × 2 symmetric matrix with integer entries. Then M is invertible ifa)The first column of M is the transpose of the second row of Mb)The second row of M is the transpose of the first column of Mc)M is a diagonal matrix with non-zero entries in the main diagonald)The product of entries in the main diagonal of M is not the square of an integerCorrect answer is option 'C,D'. Can you explain this answer? covers all topics & solutions for JEE 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for Let M be a 2 × 2 symmetric matrix with integer entries. Then M is invertible ifa)The first column of M is the transpose of the second row of Mb)The second row of M is the transpose of the first column of Mc)M is a diagonal matrix with non-zero entries in the main diagonald)The product of entries in the main diagonal of M is not the square of an integerCorrect answer is option 'C,D'. Can you explain this answer?.
Let M be a 2 × 2 symmetric matrix with integer entries. Then M is invertible ifa)The first column of M is the transpose of the second row of Mb)The second row of M is the transpose of the first column of Mc)M is a diagonal matrix with non-zero entries in the main diagonald)The product of entries in the main diagonal of M is not the square of an integerCorrect answer is option 'C,D'. Can you explain this answer? for JEE 2024 is part of JEE preparation. The Question and answers have been prepared according to the JEE exam syllabus. Information about Let M be a 2 × 2 symmetric matrix with integer entries. Then M is invertible ifa)The first column of M is the transpose of the second row of Mb)The second row of M is the transpose of the first column of Mc)M is a diagonal matrix with non-zero entries in the main diagonald)The product of entries in the main diagonal of M is not the square of an integerCorrect answer is option 'C,D'. Can you explain this answer? covers all topics & solutions for JEE 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for Let M be a 2 × 2 symmetric matrix with integer entries. Then M is invertible ifa)The first column of M is the transpose of the second row of Mb)The second row of M is the transpose of the first column of Mc)M is a diagonal matrix with non-zero entries in the main diagonald)The product of entries in the main diagonal of M is not the square of an integerCorrect answer is option 'C,D'. Can you explain this answer?.
Solutions for Let M be a 2 × 2 symmetric matrix with integer entries. Then M is invertible ifa)The first column of M is the transpose of the second row of Mb)The second row of M is the transpose of the first column of Mc)M is a diagonal matrix with non-zero entries in the main diagonald)The product of entries in the main diagonal of M is not the square of an integerCorrect answer is option 'C,D'. Can you explain this answer? in English & in Hindi are available as part of our courses for JEE.
Download more important topics, notes, lectures and mock test series for JEE Exam by signing up for free.
Here you can find the meaning of Let M be a 2 × 2 symmetric matrix with integer entries. Then M is invertible ifa)The first column of M is the transpose of the second row of Mb)The second row of M is the transpose of the first column of Mc)M is a diagonal matrix with non-zero entries in the main diagonald)The product of entries in the main diagonal of M is not the square of an integerCorrect answer is option 'C,D'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
Let M be a 2 × 2 symmetric matrix with integer entries. Then M is invertible ifa)The first column of M is the transpose of the second row of Mb)The second row of M is the transpose of the first column of Mc)M is a diagonal matrix with non-zero entries in the main diagonald)The product of entries in the main diagonal of M is not the square of an integerCorrect answer is option 'C,D'. Can you explain this answer?, a detailed solution for Let M be a 2 × 2 symmetric matrix with integer entries. Then M is invertible ifa)The first column of M is the transpose of the second row of Mb)The second row of M is the transpose of the first column of Mc)M is a diagonal matrix with non-zero entries in the main diagonald)The product of entries in the main diagonal of M is not the square of an integerCorrect answer is option 'C,D'. Can you explain this answer? has been provided alongside types of Let M be a 2 × 2 symmetric matrix with integer entries. Then M is invertible ifa)The first column of M is the transpose of the second row of Mb)The second row of M is the transpose of the first column of Mc)M is a diagonal matrix with non-zero entries in the main diagonald)The product of entries in the main diagonal of M is not the square of an integerCorrect answer is option 'C,D'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice Let M be a 2 × 2 symmetric matrix with integer entries. Then M is invertible ifa)The first column of M is the transpose of the second row of Mb)The second row of M is the transpose of the first column of Mc)M is a diagonal matrix with non-zero entries in the main diagonald)The product of entries in the main diagonal of M is not the square of an integerCorrect answer is option 'C,D'. Can you explain this answer? tests, examples and also practice JEE tests.
|
|
Explore Courses for JEE exam
|
|
Suggested Free Tests
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.
|
© EduRev
|
Education Revolution
|
Follow Us
|
Signup to see your scores
go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup