A motorist used 15% of his fuel to cover 30% of his total journey. He covered another 40% of his total journey under similar conditions. For the rest of the journey conditions were different. Find the maximum percentage by which his fuel efficiency can drop, so that he can still cover the remaining journey without refill.Note: Fuel efficiency = distance covered per unit quantity of fuel.a)76.92%b)71.45%c)79.13%d)None of theseCorrect answer is option 'A'. Can you explain this answer?

Explore Courses UPSC Exam UPSC Test Series Free Notes EduRev Infinity

Open App

CAT Exam > CAT Questions > A motorist used 15% of his fuel to cover 30% ...

A motorist used 15% of his fuel to cover 30% of his total journey. He covered another 40% of his total journey under similar conditions. For the rest of the journey conditions were different. Find the maximum percentage by which his fuel efficiency can drop, so that he can still cover the remaining journey without refill.Note: Fuel efficiency = distance covered per unit quantity of fuel.

a)
76.92%
b)
71.45%
c)
79.13%
d)
None of these

Correct answer is option 'A'. Can you explain this answer?

Join for Free

Join for Free

Verified Answer

A motorist used 15% of his fuel to cover 30% of his total journey. He ...

Let total fuel and total distance be 100 litres and 100 km respectively.

He covers 30 km in 15 litres.

Similarly, He covers 40 km in 20 litres.
Efficiency = Total distance/Total fuel consumption = 70/35 = 2 Remaining distance = 30 and remaining fuel = 65 litres.
Now, He will travel 30 km in 65 litres.

∴ Efficiency = 30/65 = 6/13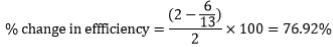

Hence, option 1.

View all questions of this test

Most Upvoted Answer

A motorist used 15% of his fuel to cover 30% of his total journey. He ...

To find the maximum percentage by which the motorist's fuel efficiency can drop, we need to analyze the given information step by step.

Step 1: Calculate the distance covered using 15% of fuel
Let's assume the total distance of the journey as D.
The motorist used 15% of his fuel to cover 30% of the total journey.
So, the distance covered using 15% of the fuel = 0.3D
Let's call this distance as D1.

Step 2: Calculate the distance covered using another 40% of fuel
The motorist covered another 40% of the total journey using similar conditions.
So, the distance covered using another 40% of the fuel = 0.4D
Let's call this distance as D2.

Step 3: Calculate the remaining distance
The remaining distance can be calculated by subtracting the distances covered (D1 + D2) from the total distance (D).
Remaining distance = D - (D1 + D2)

Step 4: Calculate the remaining fuel efficiency
To calculate the remaining fuel efficiency, we need to find the ratio of the remaining distance to the remaining fuel.
Let's assume the remaining fuel efficiency as E.
Remaining fuel efficiency E = (Remaining distance) / (Remaining fuel)

Step 5: Find the maximum percentage by which fuel efficiency can drop
To find the maximum percentage, we need to compare the remaining fuel efficiency (E) to the initial fuel efficiency (100%).
Let's calculate the maximum percentage by which fuel efficiency can drop using the formula:
Maximum percentage = ((Initial fuel efficiency - Remaining fuel efficiency) / Initial fuel efficiency) * 100

Let's summarize the calculations:

- Distance covered using 15% of fuel (D1) = 0.3D
- Distance covered using another 40% of fuel (D2) = 0.4D
- Remaining distance = D - (D1 + D2)
- Remaining fuel efficiency E = (Remaining distance) / (Remaining fuel)
- Maximum percentage = ((100% - E) / 100%) * 100

Now, let's substitute the values and calculate the maximum percentage.

From step 1, we know that D1 = 0.3D
From step 2, we know that D2 = 0.4D
From step 3, we know that Remaining distance = D - (D1 + D2) = D - (0.3D + 0.4D) = D - 0.7D = 0.3D
From step 4, we know that Remaining fuel efficiency E = (Remaining distance) / (Remaining fuel) = (0.3D) / (0.3D) = 1

Substituting the values in the formula of maximum percentage, we get:
Maximum percentage = ((100% - 1) / 100%) * 100 = (99 / 100) * 100 = 99%

Therefore, the maximum percentage by which the motorist's fuel efficiency can drop is 99%.

This does not match with any of the given options (a, b, c, d).
Hence, the correct answer cannot be determined from the given options.

Answered by Wizius Careers · View profile

Free Test

FREE

Test: CAT Quantitative Aptitude- 7
22 Ques | 40 Min

Start Free Test

View all free CAT tests

Community Answer

A motorist used 15% of his fuel to cover 30% of his total journey. He ...

Elaborate more i didn't get the last part

View all answers Start learning for free

Explore Courses for CAT exam

Similar CAT Doubts

A motorist uses 24% of his fuel in covering the first 20% of his total journey (in city driving conditions). He has to cover another 25% of his total journey in city driving conditions. What should be the minimum percentage increase in fuel efficiency for non-city driving over that in city driving, so that he is just able to cover his entire journey without having to refuel?

View answer

Answer the following question based on the information given below.Vijay has just started saving enough money and he wants to learn how to invest it in the best possible manner. His friend Amit has agreed to help him. Amit tells Vijay that he invests his money in four broad categories: fixed deposits, equities, equity mutual funds and debt mutual funds. Amit saves Rs. 40,000 every year and deposits all of it across these four categories on 1st April of every year. He started investing in 2004 with equal amounts in the four categories, but since then, the break-up of his deposits across these four categories has differed. However, he ensures that 50% of his yearly savings go into equities and equity mutual funds and the remaining 50% in the other 2 categories.Also, Amit maintains a data table recording the total amount he has in each of these fourcategories as on 1st April of every year (table given below). It is also known that the interest rates on fixed deposits have been decreasing: they were 10%, 9% and 8% per annum in the years 2004-05, 2005-06, and 2006-07 respectively. Amit also remembers that the percentage returns on equities in 2006-07 were five times the percentage returns on debt mutual funds in the same year and the percentage returns on equity mutual funds in 2004-05 and 2005-06 were half of the percentage returns on equities in 2005-06 and 2006-07 respectively. Amit does not remember too many details besides that.Q. What were the percentage returns on equities in the year 2004-05? Correct answer is '30'. Can you explain this answer?

View answer

Vijay has just started saving enough money and he wants to learn how to invest it in the best possible manner. His friend Amit has agreed to help him. Amit tells Vijay that he invests his money in four broad categories: fixed deposits, equities, equity mutual funds and debt mutual funds. Amit saves Rs. 40,000 every year and deposits all of it across these four categories on 1st April of every year. He started investing in 2004 with equal amounts in the four categories, but since then, the break-up of his deposits across these four categories has differed. However, he ensures that 50% of his yearly savings go into equities and equity mutual funds and the remaining 50% in the other 2 categories.Also, Amit maintains a data table recording the total amount he has in each of these fourcategories as on 1st April of every year (table given below). It is also known that the interest rates on fixed deposits have been decreasing: they were 10%, 9% and 8% per annum in the years 2004-05, 2005-06, and 2006-07 respectively. Amit also remembers that the percentage returns on equities in 2006-07 were five times the percentage returns on debt mutual funds in the same year and the percentage returns on equity mutual funds in 2004-05 and 2005-06 were half of the percentage returns on equities in 2005-06 and 2006-07 respectively. Amit does not remember too many details besides that.Q. What were the percentage returns on debt mutual funds in the year 2005-06? Correct answer is '12'. Can you explain this answer?

View answer

For a particular industry, Supply Efficiency is measured in terms of the actual supply of a product as a percentage of its demand. Similarly, the Market Potential measures the demand for a product compared in percentage terms to the production capacity for that product. The graph below shows the Supply Efficiency and Market Potential for a product in this industry.Q. Which of these years shows the highest increase in the difference between the Production Capacity and Supply over the previous year, if the Demand for the product is 80000 tons for each year?

View answer

Directorate of Techincal Education (DTE) holds an admission counseling round. DTE categorizes the institutes in four different types A, B, C and D. DTE also divides the students into four categories according to their percentiles. In each type of institute, a certain number of seats are reserved for each percentile range and each student has to select exactly one type of institute as their choice. Table 1 shows the percentage breakup of students of various categories interested in the different categories of colleges. Table 2 shows the number of students interested per seat. Table 3 shows the number of colleges in each category and the number of students per college. Table 1 : Percentage of students interested in a college category with respect to the number of students with the same range of percentiles.Table 2 : Students interested per seatTable 3 : Number of seats in an institute and number of institute in a category of college the students with 80 and above percentileQ. What percentage of students who are interested in category C have 85-90 percentile?

View answer

Top Courses for CATView all

Quantitative Aptitude (Quant)

CAT Mock Test Series 2025

Crash Course for CAT

Mock Test Series for SNAP

Mock Test Series for XAT

Top Courses for CAT

View all

Share with a Friend

Answer this doubt

Question Description
A motorist used 15% of his fuel to cover 30% of his total journey. He covered another 40% of his total journey under similar conditions. For the rest of the journey conditions were different. Find the maximum percentage by which his fuel efficiency can drop, so that he can still cover the remaining journey without refill.Note: Fuel efficiency = distance covered per unit quantity of fuel.a)76.92%b)71.45%c)79.13%d)None of theseCorrect answer is option 'A'. Can you explain this answer? for CAT 2025 is part of CAT preparation. The Question and answers have been prepared according to the CAT exam syllabus. Information about A motorist used 15% of his fuel to cover 30% of his total journey. He covered another 40% of his total journey under similar conditions. For the rest of the journey conditions were different. Find the maximum percentage by which his fuel efficiency can drop, so that he can still cover the remaining journey without refill.Note: Fuel efficiency = distance covered per unit quantity of fuel.a)76.92%b)71.45%c)79.13%d)None of theseCorrect answer is option 'A'. Can you explain this answer? covers all topics & solutions for CAT 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for A motorist used 15% of his fuel to cover 30% of his total journey. He covered another 40% of his total journey under similar conditions. For the rest of the journey conditions were different. Find the maximum percentage by which his fuel efficiency can drop, so that he can still cover the remaining journey without refill.Note: Fuel efficiency = distance covered per unit quantity of fuel.a)76.92%b)71.45%c)79.13%d)None of theseCorrect answer is option 'A'. Can you explain this answer?.

Solutions for A motorist used 15% of his fuel to cover 30% of his total journey. He covered another 40% of his total journey under similar conditions. For the rest of the journey conditions were different. Find the maximum percentage by which his fuel efficiency can drop, so that he can still cover the remaining journey without refill.Note: Fuel efficiency = distance covered per unit quantity of fuel.a)76.92%b)71.45%c)79.13%d)None of theseCorrect answer is option 'A'. Can you explain this answer? in English & in Hindi are available as part of our courses for CAT. Download more important topics, notes, lectures and mock test series for CAT Exam by signing up for free.

Here you can find the meaning of A motorist used 15% of his fuel to cover 30% of his total journey. He covered another 40% of his total journey under similar conditions. For the rest of the journey conditions were different. Find the maximum percentage by which his fuel efficiency can drop, so that he can still cover the remaining journey without refill.Note: Fuel efficiency = distance covered per unit quantity of fuel.a)76.92%b)71.45%c)79.13%d)None of theseCorrect answer is option 'A'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of A motorist used 15% of his fuel to cover 30% of his total journey. He covered another 40% of his total journey under similar conditions. For the rest of the journey conditions were different. Find the maximum percentage by which his fuel efficiency can drop, so that he can still cover the remaining journey without refill.Note: Fuel efficiency = distance covered per unit quantity of fuel.a)76.92%b)71.45%c)79.13%d)None of theseCorrect answer is option 'A'. Can you explain this answer?, a detailed solution for A motorist used 15% of his fuel to cover 30% of his total journey. He covered another 40% of his total journey under similar conditions. For the rest of the journey conditions were different. Find the maximum percentage by which his fuel efficiency can drop, so that he can still cover the remaining journey without refill.Note: Fuel efficiency = distance covered per unit quantity of fuel.a)76.92%b)71.45%c)79.13%d)None of theseCorrect answer is option 'A'. Can you explain this answer? has been provided alongside types of A motorist used 15% of his fuel to cover 30% of his total journey. He covered another 40% of his total journey under similar conditions. For the rest of the journey conditions were different. Find the maximum percentage by which his fuel efficiency can drop, so that he can still cover the remaining journey without refill.Note: Fuel efficiency = distance covered per unit quantity of fuel.a)76.92%b)71.45%c)79.13%d)None of theseCorrect answer is option 'A'. Can you explain this answer? theory, EduRev gives you an ample number of questions to practice A motorist used 15% of his fuel to cover 30% of his total journey. He covered another 40% of his total journey under similar conditions. For the rest of the journey conditions were different. Find the maximum percentage by which his fuel efficiency can drop, so that he can still cover the remaining journey without refill.Note: Fuel efficiency = distance covered per unit quantity of fuel.a)76.92%b)71.45%c)79.13%d)None of theseCorrect answer is option 'A'. Can you explain this answer? tests, examples and also practice CAT tests.

Explore Courses for CAT exam