Computer Science Engineering (CSE) Exam > Computer Science Engineering (CSE) Questions > A complete binary tree with n non-leaf nodes ...
Start Learning for Free
A complete binary tree with n non-leaf nodes contains
- a)log2 n nodes
- b)n + 1 nodes
- c)2n nodes
- d)2n + 1 nodes
Correct answer is option 'D'. Can you explain this answer?
Verified Answer
A complete binary tree with n non-leaf nodes containsa)log2 n nodesb)n...
In complete binary tree.
Number of internal nodes = No. of leaf node - 1
So total number of nodes = Internal nodes + Leaf node
Number of internal nodes = No. of leaf node - 1
So total number of nodes = Internal nodes + Leaf node

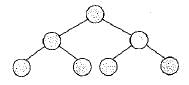
Most Upvoted Answer
A complete binary tree with n non-leaf nodes containsa)log2 n nodesb)n...
Explanation:
To understand why option D is the correct answer, let's first define what a complete binary tree is and how it is related to non-leaf nodes.
Complete Binary Tree:
A binary tree is said to be complete if all levels of the tree are completely filled except possibly the last level, which is filled from left to right. In other words, a complete binary tree is a binary tree in which all nodes have either 0 or 2 children, except for the last level which may have only 1 child.
Non-Leaf Nodes:
Non-leaf nodes in a binary tree are those nodes that have at least one child. These nodes are also known as internal nodes.
Now, let's analyze the options provided in the question and determine which one is correct.
Option A: log2 n nodes
This option suggests that the number of nodes in a complete binary tree with n non-leaf nodes is equal to log2 n. However, this is incorrect because the number of nodes in a complete binary tree is related to the height of the tree, not the number of non-leaf nodes.
Option B: n - 1 nodes
This option suggests that the number of nodes in a complete binary tree with n non-leaf nodes is equal to n - 1. Again, this is incorrect because the number of nodes in a complete binary tree is not directly dependent on the number of non-leaf nodes.
Option C: 2n nodes
This option suggests that the number of nodes in a complete binary tree with n non-leaf nodes is equal to 2n. This is incorrect because 2n would include both leaf and non-leaf nodes.
Option D: 2n - 1 nodes
This option suggests that the number of nodes in a complete binary tree with n non-leaf nodes is equal to 2n - 1. This is the correct answer. Here's why:
- In a complete binary tree, the number of leaf nodes is always one more than the number of non-leaf nodes.
- So, if we have n non-leaf nodes, we will have n + 1 leaf nodes.
- Each leaf node is also a non-leaf node in the next level.
- Therefore, the total number of nodes in a complete binary tree with n non-leaf nodes is 2n + (n + 1) = 2n + n + 1 = 3n + 1.
- But since we only need to consider non-leaf nodes, the number of nodes in the complete binary tree with n non-leaf nodes is 3n.
- Subtracting 1 from this count (to exclude the root node) gives us 3n - 1, which is equal to 2n - 1.
Hence, option D is the correct answer.
To understand why option D is the correct answer, let's first define what a complete binary tree is and how it is related to non-leaf nodes.
Complete Binary Tree:
A binary tree is said to be complete if all levels of the tree are completely filled except possibly the last level, which is filled from left to right. In other words, a complete binary tree is a binary tree in which all nodes have either 0 or 2 children, except for the last level which may have only 1 child.
Non-Leaf Nodes:
Non-leaf nodes in a binary tree are those nodes that have at least one child. These nodes are also known as internal nodes.
Now, let's analyze the options provided in the question and determine which one is correct.
Option A: log2 n nodes
This option suggests that the number of nodes in a complete binary tree with n non-leaf nodes is equal to log2 n. However, this is incorrect because the number of nodes in a complete binary tree is related to the height of the tree, not the number of non-leaf nodes.
Option B: n - 1 nodes
This option suggests that the number of nodes in a complete binary tree with n non-leaf nodes is equal to n - 1. Again, this is incorrect because the number of nodes in a complete binary tree is not directly dependent on the number of non-leaf nodes.
Option C: 2n nodes
This option suggests that the number of nodes in a complete binary tree with n non-leaf nodes is equal to 2n. This is incorrect because 2n would include both leaf and non-leaf nodes.
Option D: 2n - 1 nodes
This option suggests that the number of nodes in a complete binary tree with n non-leaf nodes is equal to 2n - 1. This is the correct answer. Here's why:
- In a complete binary tree, the number of leaf nodes is always one more than the number of non-leaf nodes.
- So, if we have n non-leaf nodes, we will have n + 1 leaf nodes.
- Each leaf node is also a non-leaf node in the next level.
- Therefore, the total number of nodes in a complete binary tree with n non-leaf nodes is 2n + (n + 1) = 2n + n + 1 = 3n + 1.
- But since we only need to consider non-leaf nodes, the number of nodes in the complete binary tree with n non-leaf nodes is 3n.
- Subtracting 1 from this count (to exclude the root node) gives us 3n - 1, which is equal to 2n - 1.
Hence, option D is the correct answer.

|
Explore Courses for Computer Science Engineering (CSE) exam
|

|
Question Description
A complete binary tree with n non-leaf nodes containsa)log2 n nodesb)n + 1 nodesc)2n nodesd)2n + 1 nodesCorrect answer is option 'D'. Can you explain this answer? for Computer Science Engineering (CSE) 2025 is part of Computer Science Engineering (CSE) preparation. The Question and answers have been prepared according to the Computer Science Engineering (CSE) exam syllabus. Information about A complete binary tree with n non-leaf nodes containsa)log2 n nodesb)n + 1 nodesc)2n nodesd)2n + 1 nodesCorrect answer is option 'D'. Can you explain this answer? covers all topics & solutions for Computer Science Engineering (CSE) 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for A complete binary tree with n non-leaf nodes containsa)log2 n nodesb)n + 1 nodesc)2n nodesd)2n + 1 nodesCorrect answer is option 'D'. Can you explain this answer?.
A complete binary tree with n non-leaf nodes containsa)log2 n nodesb)n + 1 nodesc)2n nodesd)2n + 1 nodesCorrect answer is option 'D'. Can you explain this answer? for Computer Science Engineering (CSE) 2025 is part of Computer Science Engineering (CSE) preparation. The Question and answers have been prepared according to the Computer Science Engineering (CSE) exam syllabus. Information about A complete binary tree with n non-leaf nodes containsa)log2 n nodesb)n + 1 nodesc)2n nodesd)2n + 1 nodesCorrect answer is option 'D'. Can you explain this answer? covers all topics & solutions for Computer Science Engineering (CSE) 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for A complete binary tree with n non-leaf nodes containsa)log2 n nodesb)n + 1 nodesc)2n nodesd)2n + 1 nodesCorrect answer is option 'D'. Can you explain this answer?.
Solutions for A complete binary tree with n non-leaf nodes containsa)log2 n nodesb)n + 1 nodesc)2n nodesd)2n + 1 nodesCorrect answer is option 'D'. Can you explain this answer? in English & in Hindi are available as part of our courses for Computer Science Engineering (CSE).
Download more important topics, notes, lectures and mock test series for Computer Science Engineering (CSE) Exam by signing up for free.
Here you can find the meaning of A complete binary tree with n non-leaf nodes containsa)log2 n nodesb)n + 1 nodesc)2n nodesd)2n + 1 nodesCorrect answer is option 'D'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
A complete binary tree with n non-leaf nodes containsa)log2 n nodesb)n + 1 nodesc)2n nodesd)2n + 1 nodesCorrect answer is option 'D'. Can you explain this answer?, a detailed solution for A complete binary tree with n non-leaf nodes containsa)log2 n nodesb)n + 1 nodesc)2n nodesd)2n + 1 nodesCorrect answer is option 'D'. Can you explain this answer? has been provided alongside types of A complete binary tree with n non-leaf nodes containsa)log2 n nodesb)n + 1 nodesc)2n nodesd)2n + 1 nodesCorrect answer is option 'D'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice A complete binary tree with n non-leaf nodes containsa)log2 n nodesb)n + 1 nodesc)2n nodesd)2n + 1 nodesCorrect answer is option 'D'. Can you explain this answer? tests, examples and also practice Computer Science Engineering (CSE) tests.

|
Explore Courses for Computer Science Engineering (CSE) exam
|

|
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.


















