Mathematics Exam > Mathematics Questions > Which of the following is not correct?a)The s...
Start Learning for Free
Which of the following is not correct?
- a)The set R of real number is uncountable
- b)The set of rational number in [0, 1] is countable
- c)The set of all rational numbers is countable
- d)None of the above
Correct answer is option 'D'. Can you explain this answer?
| FREE This question is part of | Download PDF Attempt this Test |
Verified Answer
Which of the following is not correct?a)The set R of real number is un...
Let us suppose that the set of real num ber R is countable, then R = {x1, x2, ..., xn, ...}. Enclose each member xn of R in an open interval In =
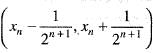of length 
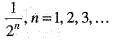where the sum of lengths of In's is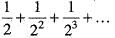 
But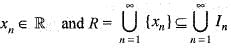
Implies, The whole real line is contained in the union of intervals whose lengths add up to 1. Which is a contradiction. Hence, R is uncountable.
Arrange the set of rationals according to increasing denominators as
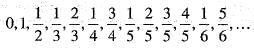Then the one-one correspondence can be indicated as
which shows that the set of rational number in [0, 1] is countable. Now, the set of all rational numbers is the union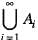 
, where Ai is the set of rationals which can be written with denominator i. Then is A, =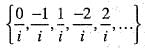 
Each Ai' is equivalent to the set of all positive integers and hence countable.
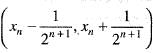of length 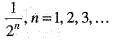where the sum of lengths of In's is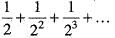 But
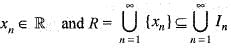
Implies, The whole real line is contained in the union of intervals whose lengths add up to 1. Which is a contradiction. Hence, R is uncountable.
Arrange the set of rationals according to increasing denominators as
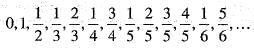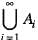Then the one-one correspondence can be indicated aswhich shows that the set of rational number in [0, 1] is countable. Now, the set of all rational numbers is the union , where Ai is the set of rationals which can be written with denominator i. Then is A, =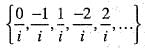 Each Ai' is equivalent to the set of all positive integers and hence countable.
Most Upvoted Answer
Which of the following is not correct?a)The set R of real number is un...
Answer:
The correct answer is option 'D' which states that none of the above statements is incorrect. Let's analyze each statement to understand why option 'D' is the correct answer.
a) The set R of real numbers is uncountable:
This statement is correct. The set of real numbers, denoted by R, is uncountable. This means that there is no one-to-one correspondence between the elements of the set and the natural numbers. The proof of this fact is known as Cantor's diagonal argument, which shows that any attempt to list all the real numbers between 0 and 1 will inevitably miss some numbers.
b) The set of rational numbers in [0, 1] is countable:
This statement is correct. The set of rational numbers in the interval [0, 1] is countable. A set is countable if its elements can be put into a one-to-one correspondence with the natural numbers. The rational numbers can be listed by arranging them in a grid, where each row represents a fraction in its simplest form. By following a specific pattern, we can assign a unique natural number to each rational number in [0, 1].
c) The set of all rational numbers is countable:
This statement is also correct. The set of all rational numbers is countable. We can use a similar method as mentioned in statement (b) to list all the rational numbers. By arranging the fractions in a grid, we can assign a unique natural number to each rational number.
Explanation of option 'D':
Since all the given statements (a, b, c) are correct, the correct answer is option 'D' which states that none of the above statements is incorrect. This means that all the statements are true and there is no incorrect statement among them.
In conclusion, the correct answer is option 'D' - None of the above.
The correct answer is option 'D' which states that none of the above statements is incorrect. Let's analyze each statement to understand why option 'D' is the correct answer.
a) The set R of real numbers is uncountable:
This statement is correct. The set of real numbers, denoted by R, is uncountable. This means that there is no one-to-one correspondence between the elements of the set and the natural numbers. The proof of this fact is known as Cantor's diagonal argument, which shows that any attempt to list all the real numbers between 0 and 1 will inevitably miss some numbers.
b) The set of rational numbers in [0, 1] is countable:
This statement is correct. The set of rational numbers in the interval [0, 1] is countable. A set is countable if its elements can be put into a one-to-one correspondence with the natural numbers. The rational numbers can be listed by arranging them in a grid, where each row represents a fraction in its simplest form. By following a specific pattern, we can assign a unique natural number to each rational number in [0, 1].
c) The set of all rational numbers is countable:
This statement is also correct. The set of all rational numbers is countable. We can use a similar method as mentioned in statement (b) to list all the rational numbers. By arranging the fractions in a grid, we can assign a unique natural number to each rational number.
Explanation of option 'D':
Since all the given statements (a, b, c) are correct, the correct answer is option 'D' which states that none of the above statements is incorrect. This means that all the statements are true and there is no incorrect statement among them.
In conclusion, the correct answer is option 'D' - None of the above.
|
Explore Courses for Mathematics exam
|
|
Which of the following is not correct?a)The set R of real number is uncountableb)The set of rational number in [0, 1] is countablec)The set of all rational numbers is countabled)None of the aboveCorrect answer is option 'D'. Can you explain this answer?
Question Description
Which of the following is not correct?a)The set R of real number is uncountableb)The set of rational number in [0, 1] is countablec)The set of all rational numbers is countabled)None of the aboveCorrect answer is option 'D'. Can you explain this answer? for Mathematics 2024 is part of Mathematics preparation. The Question and answers have been prepared according to the Mathematics exam syllabus. Information about Which of the following is not correct?a)The set R of real number is uncountableb)The set of rational number in [0, 1] is countablec)The set of all rational numbers is countabled)None of the aboveCorrect answer is option 'D'. Can you explain this answer? covers all topics & solutions for Mathematics 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for Which of the following is not correct?a)The set R of real number is uncountableb)The set of rational number in [0, 1] is countablec)The set of all rational numbers is countabled)None of the aboveCorrect answer is option 'D'. Can you explain this answer?.
Which of the following is not correct?a)The set R of real number is uncountableb)The set of rational number in [0, 1] is countablec)The set of all rational numbers is countabled)None of the aboveCorrect answer is option 'D'. Can you explain this answer? for Mathematics 2024 is part of Mathematics preparation. The Question and answers have been prepared according to the Mathematics exam syllabus. Information about Which of the following is not correct?a)The set R of real number is uncountableb)The set of rational number in [0, 1] is countablec)The set of all rational numbers is countabled)None of the aboveCorrect answer is option 'D'. Can you explain this answer? covers all topics & solutions for Mathematics 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for Which of the following is not correct?a)The set R of real number is uncountableb)The set of rational number in [0, 1] is countablec)The set of all rational numbers is countabled)None of the aboveCorrect answer is option 'D'. Can you explain this answer?.
Solutions for Which of the following is not correct?a)The set R of real number is uncountableb)The set of rational number in [0, 1] is countablec)The set of all rational numbers is countabled)None of the aboveCorrect answer is option 'D'. Can you explain this answer? in English & in Hindi are available as part of our courses for Mathematics.
Download more important topics, notes, lectures and mock test series for Mathematics Exam by signing up for free.
Here you can find the meaning of Which of the following is not correct?a)The set R of real number is uncountableb)The set of rational number in [0, 1] is countablec)The set of all rational numbers is countabled)None of the aboveCorrect answer is option 'D'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
Which of the following is not correct?a)The set R of real number is uncountableb)The set of rational number in [0, 1] is countablec)The set of all rational numbers is countabled)None of the aboveCorrect answer is option 'D'. Can you explain this answer?, a detailed solution for Which of the following is not correct?a)The set R of real number is uncountableb)The set of rational number in [0, 1] is countablec)The set of all rational numbers is countabled)None of the aboveCorrect answer is option 'D'. Can you explain this answer? has been provided alongside types of Which of the following is not correct?a)The set R of real number is uncountableb)The set of rational number in [0, 1] is countablec)The set of all rational numbers is countabled)None of the aboveCorrect answer is option 'D'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice Which of the following is not correct?a)The set R of real number is uncountableb)The set of rational number in [0, 1] is countablec)The set of all rational numbers is countabled)None of the aboveCorrect answer is option 'D'. Can you explain this answer? tests, examples and also practice Mathematics tests.
|
|
Explore Courses for Mathematics exam
|
|
Suggested Free Tests
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.
|
© EduRev
|
Education Revolution
|
Follow Us
|
Signup to see your scores
go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup