Physics Exam > Physics Questions > Which of the following is true for a quantum ...
Start Learning for Free
Which of the following is true for a quantum harmonic oscillator?
- a)A spectrum of evenly spaced energy levels
- b)A non zero probability of finding the oscillator outside the classical turning points
- c)A ground state that is characterized by zero kinetic energy.
- d)A potential energy function that is linear in the position coordinate
Correct answer is option 'A,B'. Can you explain this answer?
Most Upvoted Answer
Which of the following is true for a quantum harmonic oscillator?a)A s...
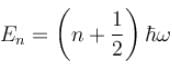 for a harmonic oscillator
for a harmonic oscillator
∴ evenly spaced.
The correct answers are: A spectrum of evenly spaced energy levels, A non zero probability of finding the oscillator outside the classical turning points
Free Test
FREE
| Start Free Test |
Community Answer
Which of the following is true for a quantum harmonic oscillator?a)A s...
Quantum Harmonic Oscillator
The quantum harmonic oscillator is a fundamental concept in quantum mechanics that describes a particle subject to a restoring force proportional to its displacement from equilibrium. It has a potential energy function that is quadratic in the position coordinate and is given by V(x) = 1/2 kx^2, where k is the spring constant.
Spectrum of Evenly Spaced Energy Levels
One of the key properties of the quantum harmonic oscillator is that it exhibits a spectrum of evenly spaced energy levels. This means that the energy levels of the oscillator are quantized, with each level corresponding to a specific energy value. The energy levels are given by E_n = (n + 1/2) ħω, where n is a non-negative integer and ħ is the reduced Planck's constant. The energy spacing between consecutive levels is constant and equal to ħω, where ω is the angular frequency of the oscillator.
Non-zero Probability of Finding the Oscillator Outside Classical Turning Points
The classical turning points of a harmonic oscillator correspond to the points where the particle momentarily comes to rest before changing direction. In classical mechanics, a particle cannot exist outside these turning points. However, in quantum mechanics, the wave nature of particles allows for a non-zero probability of finding the oscillator outside the classical turning points. This is because the position of the particle in quantum mechanics is described by a probability distribution, represented by the wavefunction. The wavefunction can extend beyond the classical turning points, indicating a non-zero probability of finding the particle in those regions.
Ground State with Zero Kinetic Energy
The ground state of a quantum harmonic oscillator corresponds to the lowest energy level. In this state, the particle has the lowest possible energy. However, contrary to option C, the ground state does not have zero kinetic energy. In fact, the ground state has the lowest possible energy while maintaining a balance between its kinetic and potential energy. The ground state wavefunction is a Gaussian function centered around the equilibrium position, and it exhibits oscillatory behavior.
Potential Energy Function
The potential energy function of a quantum harmonic oscillator is quadratic in the position coordinate, as mentioned earlier. The potential energy increases quadratically as the particle is displaced from its equilibrium position. It is not linear in the position coordinate, so option D is incorrect.
To summarize, the true statements about a quantum harmonic oscillator are:
- It exhibits a spectrum of evenly spaced energy levels.
- It has a non-zero probability of finding the oscillator outside the classical turning points.
The quantum harmonic oscillator is a fundamental concept in quantum mechanics that describes a particle subject to a restoring force proportional to its displacement from equilibrium. It has a potential energy function that is quadratic in the position coordinate and is given by V(x) = 1/2 kx^2, where k is the spring constant.
Spectrum of Evenly Spaced Energy Levels
One of the key properties of the quantum harmonic oscillator is that it exhibits a spectrum of evenly spaced energy levels. This means that the energy levels of the oscillator are quantized, with each level corresponding to a specific energy value. The energy levels are given by E_n = (n + 1/2) ħω, where n is a non-negative integer and ħ is the reduced Planck's constant. The energy spacing between consecutive levels is constant and equal to ħω, where ω is the angular frequency of the oscillator.
Non-zero Probability of Finding the Oscillator Outside Classical Turning Points
The classical turning points of a harmonic oscillator correspond to the points where the particle momentarily comes to rest before changing direction. In classical mechanics, a particle cannot exist outside these turning points. However, in quantum mechanics, the wave nature of particles allows for a non-zero probability of finding the oscillator outside the classical turning points. This is because the position of the particle in quantum mechanics is described by a probability distribution, represented by the wavefunction. The wavefunction can extend beyond the classical turning points, indicating a non-zero probability of finding the particle in those regions.
Ground State with Zero Kinetic Energy
The ground state of a quantum harmonic oscillator corresponds to the lowest energy level. In this state, the particle has the lowest possible energy. However, contrary to option C, the ground state does not have zero kinetic energy. In fact, the ground state has the lowest possible energy while maintaining a balance between its kinetic and potential energy. The ground state wavefunction is a Gaussian function centered around the equilibrium position, and it exhibits oscillatory behavior.
Potential Energy Function
The potential energy function of a quantum harmonic oscillator is quadratic in the position coordinate, as mentioned earlier. The potential energy increases quadratically as the particle is displaced from its equilibrium position. It is not linear in the position coordinate, so option D is incorrect.
To summarize, the true statements about a quantum harmonic oscillator are:
- It exhibits a spectrum of evenly spaced energy levels.
- It has a non-zero probability of finding the oscillator outside the classical turning points.

|
Explore Courses for Physics exam
|

|
Similar Physics Doubts
Which of the following is true for a quantum harmonic oscillator?a)A spectrum of evenly spaced energy levelsb)A non zero probability of finding the oscillator outside the classical turning pointsc)A ground state that is characterized by zero kinetic energy.d)A potential energy function that is linear in the position coordinateCorrect answer is option 'A,B'. Can you explain this answer?
Question Description
Which of the following is true for a quantum harmonic oscillator?a)A spectrum of evenly spaced energy levelsb)A non zero probability of finding the oscillator outside the classical turning pointsc)A ground state that is characterized by zero kinetic energy.d)A potential energy function that is linear in the position coordinateCorrect answer is option 'A,B'. Can you explain this answer? for Physics 2025 is part of Physics preparation. The Question and answers have been prepared according to the Physics exam syllabus. Information about Which of the following is true for a quantum harmonic oscillator?a)A spectrum of evenly spaced energy levelsb)A non zero probability of finding the oscillator outside the classical turning pointsc)A ground state that is characterized by zero kinetic energy.d)A potential energy function that is linear in the position coordinateCorrect answer is option 'A,B'. Can you explain this answer? covers all topics & solutions for Physics 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for Which of the following is true for a quantum harmonic oscillator?a)A spectrum of evenly spaced energy levelsb)A non zero probability of finding the oscillator outside the classical turning pointsc)A ground state that is characterized by zero kinetic energy.d)A potential energy function that is linear in the position coordinateCorrect answer is option 'A,B'. Can you explain this answer?.
Which of the following is true for a quantum harmonic oscillator?a)A spectrum of evenly spaced energy levelsb)A non zero probability of finding the oscillator outside the classical turning pointsc)A ground state that is characterized by zero kinetic energy.d)A potential energy function that is linear in the position coordinateCorrect answer is option 'A,B'. Can you explain this answer? for Physics 2025 is part of Physics preparation. The Question and answers have been prepared according to the Physics exam syllabus. Information about Which of the following is true for a quantum harmonic oscillator?a)A spectrum of evenly spaced energy levelsb)A non zero probability of finding the oscillator outside the classical turning pointsc)A ground state that is characterized by zero kinetic energy.d)A potential energy function that is linear in the position coordinateCorrect answer is option 'A,B'. Can you explain this answer? covers all topics & solutions for Physics 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for Which of the following is true for a quantum harmonic oscillator?a)A spectrum of evenly spaced energy levelsb)A non zero probability of finding the oscillator outside the classical turning pointsc)A ground state that is characterized by zero kinetic energy.d)A potential energy function that is linear in the position coordinateCorrect answer is option 'A,B'. Can you explain this answer?.
Solutions for Which of the following is true for a quantum harmonic oscillator?a)A spectrum of evenly spaced energy levelsb)A non zero probability of finding the oscillator outside the classical turning pointsc)A ground state that is characterized by zero kinetic energy.d)A potential energy function that is linear in the position coordinateCorrect answer is option 'A,B'. Can you explain this answer? in English & in Hindi are available as part of our courses for Physics.
Download more important topics, notes, lectures and mock test series for Physics Exam by signing up for free.
Here you can find the meaning of Which of the following is true for a quantum harmonic oscillator?a)A spectrum of evenly spaced energy levelsb)A non zero probability of finding the oscillator outside the classical turning pointsc)A ground state that is characterized by zero kinetic energy.d)A potential energy function that is linear in the position coordinateCorrect answer is option 'A,B'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
Which of the following is true for a quantum harmonic oscillator?a)A spectrum of evenly spaced energy levelsb)A non zero probability of finding the oscillator outside the classical turning pointsc)A ground state that is characterized by zero kinetic energy.d)A potential energy function that is linear in the position coordinateCorrect answer is option 'A,B'. Can you explain this answer?, a detailed solution for Which of the following is true for a quantum harmonic oscillator?a)A spectrum of evenly spaced energy levelsb)A non zero probability of finding the oscillator outside the classical turning pointsc)A ground state that is characterized by zero kinetic energy.d)A potential energy function that is linear in the position coordinateCorrect answer is option 'A,B'. Can you explain this answer? has been provided alongside types of Which of the following is true for a quantum harmonic oscillator?a)A spectrum of evenly spaced energy levelsb)A non zero probability of finding the oscillator outside the classical turning pointsc)A ground state that is characterized by zero kinetic energy.d)A potential energy function that is linear in the position coordinateCorrect answer is option 'A,B'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice Which of the following is true for a quantum harmonic oscillator?a)A spectrum of evenly spaced energy levelsb)A non zero probability of finding the oscillator outside the classical turning pointsc)A ground state that is characterized by zero kinetic energy.d)A potential energy function that is linear in the position coordinateCorrect answer is option 'A,B'. Can you explain this answer? tests, examples and also practice Physics tests.

|
Explore Courses for Physics exam
|

|
Signup to solve all Doubts
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.















