Mathematics Exam > Mathematics Questions > The Euler’s method for solving a differ...
Start Learning for Free
The Euler’s method for solving a differential equation of the type dy/dx = f(x, y) provides
- a)An approximate solution in general
- b)Always an exact solution
- c)An exact solution only when the differential equation is of the type dy/dx = h(y) or g(x)
- d)None of the above
Correct answer is option 'A'. Can you explain this answer?
| FREE This question is part of | Download PDF Attempt this Test |
Verified Answer
The Euler’s method for solving a differentialequation of the typ...
Euler’s method.
This method provides the solution of the differential equations of the form
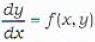
in the form of a set of tabulated values. This method is very slow and to obtain reasonable accuracy with Euler's method, h should be taken very small. This method provid es an approximate solution of equation (i) in general.
This method provides the solution of the differential equations of the form
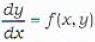
in the form of a set of tabulated values. This method is very slow and to obtain reasonable accuracy with Euler's method, h should be taken very small. This method provid es an approximate solution of equation (i) in general.
Most Upvoted Answer
The Euler’s method for solving a differentialequation of the typ...
Euler’s method.
This method provides the solution of the differential equations of the form
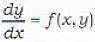
in the form of a set of tabulated values. This method is very slow and to obtain reasonable accuracy with Euler's method, h should be taken very small. This method provid es an approximate solution of equation (i) in general.
This method provides the solution of the differential equations of the form
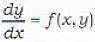
in the form of a set of tabulated values. This method is very slow and to obtain reasonable accuracy with Euler's method, h should be taken very small. This method provid es an approximate solution of equation (i) in general.
Free Test
FREE
| Start Free Test |
Community Answer
The Euler’s method for solving a differentialequation of the typ...
The Euler is a mathematical constant that is approximately equal to 2.71828. It is named after the Swiss mathematician Leonhard Euler, who made significant contributions to the field of mathematics.
The Euler is an irrational number, meaning it cannot be expressed as a fraction and its decimal representation goes on infinitely without repeating. It is also a transcendental number, which means it is not a solution to any non-zero polynomial equation with integer coefficients.
The Euler is commonly denoted by the letter "e" and is often used in mathematical formulas and equations, particularly in calculus. It has numerous applications in various branches of mathematics, including exponential growth and decay, compound interest, and differential equations.
One of the most famous formulas involving the Euler is Euler's formula, which relates the imaginary unit "i", the trigonometric functions sine and cosine, and the Euler itself:
e^(iπ) + 1 = 0
This formula is often considered one of the most beautiful and elegant equations in mathematics, as it combines five fundamental mathematical constants: e, i, π, 1, and 0.
In addition to its significance in mathematics, the Euler also has important applications in other fields, such as physics, engineering, and finance. It is used in various calculations and models to describe natural phenomena, solve complex problems, and make predictions.
Overall, the Euler is a fundamental mathematical constant that plays a crucial role in many areas of mathematics and science. Its unique properties and applications make it an essential concept for understanding and solving a wide range of problems.
The Euler is an irrational number, meaning it cannot be expressed as a fraction and its decimal representation goes on infinitely without repeating. It is also a transcendental number, which means it is not a solution to any non-zero polynomial equation with integer coefficients.
The Euler is commonly denoted by the letter "e" and is often used in mathematical formulas and equations, particularly in calculus. It has numerous applications in various branches of mathematics, including exponential growth and decay, compound interest, and differential equations.
One of the most famous formulas involving the Euler is Euler's formula, which relates the imaginary unit "i", the trigonometric functions sine and cosine, and the Euler itself:
e^(iπ) + 1 = 0
This formula is often considered one of the most beautiful and elegant equations in mathematics, as it combines five fundamental mathematical constants: e, i, π, 1, and 0.
In addition to its significance in mathematics, the Euler also has important applications in other fields, such as physics, engineering, and finance. It is used in various calculations and models to describe natural phenomena, solve complex problems, and make predictions.
Overall, the Euler is a fundamental mathematical constant that plays a crucial role in many areas of mathematics and science. Its unique properties and applications make it an essential concept for understanding and solving a wide range of problems.

|
Explore Courses for Mathematics exam
|

|
Similar Mathematics Doubts
The Euler’s method for solving a differentialequation of the type dy/dx = f(x, y)providesa)An approximate solution in generalb)Always an exact solutionc)An exact solution only when the differential equation is of the type dy/dx = h(y) or g(x)d)None of the aboveCorrect answer is option 'A'. Can you explain this answer?
Question Description
The Euler’s method for solving a differentialequation of the type dy/dx = f(x, y)providesa)An approximate solution in generalb)Always an exact solutionc)An exact solution only when the differential equation is of the type dy/dx = h(y) or g(x)d)None of the aboveCorrect answer is option 'A'. Can you explain this answer? for Mathematics 2024 is part of Mathematics preparation. The Question and answers have been prepared according to the Mathematics exam syllabus. Information about The Euler’s method for solving a differentialequation of the type dy/dx = f(x, y)providesa)An approximate solution in generalb)Always an exact solutionc)An exact solution only when the differential equation is of the type dy/dx = h(y) or g(x)d)None of the aboveCorrect answer is option 'A'. Can you explain this answer? covers all topics & solutions for Mathematics 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for The Euler’s method for solving a differentialequation of the type dy/dx = f(x, y)providesa)An approximate solution in generalb)Always an exact solutionc)An exact solution only when the differential equation is of the type dy/dx = h(y) or g(x)d)None of the aboveCorrect answer is option 'A'. Can you explain this answer?.
The Euler’s method for solving a differentialequation of the type dy/dx = f(x, y)providesa)An approximate solution in generalb)Always an exact solutionc)An exact solution only when the differential equation is of the type dy/dx = h(y) or g(x)d)None of the aboveCorrect answer is option 'A'. Can you explain this answer? for Mathematics 2024 is part of Mathematics preparation. The Question and answers have been prepared according to the Mathematics exam syllabus. Information about The Euler’s method for solving a differentialequation of the type dy/dx = f(x, y)providesa)An approximate solution in generalb)Always an exact solutionc)An exact solution only when the differential equation is of the type dy/dx = h(y) or g(x)d)None of the aboveCorrect answer is option 'A'. Can you explain this answer? covers all topics & solutions for Mathematics 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for The Euler’s method for solving a differentialequation of the type dy/dx = f(x, y)providesa)An approximate solution in generalb)Always an exact solutionc)An exact solution only when the differential equation is of the type dy/dx = h(y) or g(x)d)None of the aboveCorrect answer is option 'A'. Can you explain this answer?.
Solutions for The Euler’s method for solving a differentialequation of the type dy/dx = f(x, y)providesa)An approximate solution in generalb)Always an exact solutionc)An exact solution only when the differential equation is of the type dy/dx = h(y) or g(x)d)None of the aboveCorrect answer is option 'A'. Can you explain this answer? in English & in Hindi are available as part of our courses for Mathematics.
Download more important topics, notes, lectures and mock test series for Mathematics Exam by signing up for free.
Here you can find the meaning of The Euler’s method for solving a differentialequation of the type dy/dx = f(x, y)providesa)An approximate solution in generalb)Always an exact solutionc)An exact solution only when the differential equation is of the type dy/dx = h(y) or g(x)d)None of the aboveCorrect answer is option 'A'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
The Euler’s method for solving a differentialequation of the type dy/dx = f(x, y)providesa)An approximate solution in generalb)Always an exact solutionc)An exact solution only when the differential equation is of the type dy/dx = h(y) or g(x)d)None of the aboveCorrect answer is option 'A'. Can you explain this answer?, a detailed solution for The Euler’s method for solving a differentialequation of the type dy/dx = f(x, y)providesa)An approximate solution in generalb)Always an exact solutionc)An exact solution only when the differential equation is of the type dy/dx = h(y) or g(x)d)None of the aboveCorrect answer is option 'A'. Can you explain this answer? has been provided alongside types of The Euler’s method for solving a differentialequation of the type dy/dx = f(x, y)providesa)An approximate solution in generalb)Always an exact solutionc)An exact solution only when the differential equation is of the type dy/dx = h(y) or g(x)d)None of the aboveCorrect answer is option 'A'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice The Euler’s method for solving a differentialequation of the type dy/dx = f(x, y)providesa)An approximate solution in generalb)Always an exact solutionc)An exact solution only when the differential equation is of the type dy/dx = h(y) or g(x)d)None of the aboveCorrect answer is option 'A'. Can you explain this answer? tests, examples and also practice Mathematics tests.

|
Explore Courses for Mathematics exam
|

|
Suggested Free Tests
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.


















