CAT Exam > CAT Questions > Group QuestionAnswer the following question b...
Start Learning for Free
Group Question
Answer the following question based on the information given below.
A company has 2100 employees in all with male and female employees being in the ratio 19:16. Employees who come to office from the eastern or western part of the city use either the Metro trains or Local trains. The office also provides a bus service for people who stay far away and some employees use their own vehicles to commute to work. All the employees are classified as technical or nontechnical staff. 14% of the total employees use their own vehicles, with the ratio of the technical to non-technical staff in this group being 2 : 1. Of the remaining employees, one-third travel by Metro trains. The number of females who use their own vehicles and are technical staff is one-third of the number of males who are technical staff and use their own vehicles; as well as equal to the number of males who are non-technical staff and use their own vehicles. 20% of the total female staff is non-technical and uses the Local trains, which is equal to 80% of the female staff that is technical and uses Local trains. Of all the male employees who prefer to use the office bus, 123 are non-technical staff. The count of nontechnical male staff exceeds the technical male staff by four. The number of employees that use Local trains is three times the number of employees who use the office bus. One-seventh of the office bus users are non-technical female staff.
The ratio of males to females who are technical staff and use office bus is 5 : 4.
The number of male technical staff who use Local trains exceeds the male nontechnical staff using the same mode of transport by 11. 136 non-technical female staff use the Metro trains.
The ratio of males to females who are technical staff and use office bus is 5 : 4.
The number of male technical staff who use Local trains exceeds the male nontechnical staff using the same mode of transport by 11. 136 non-technical female staff use the Metro trains.
Q. What is the difference between the number of male technical staff who travel by trains and number of female non-technical staff who do not travel by Local trains?
- a)93
- b)118
- c)202
- d)Data inadequate
Correct answer is option 'B'. Can you explain this answer?
| FREE This question is part of | Download PDF Attempt this Test |
Verified Answer
Group QuestionAnswer the following question based on the information g...
First identify how the data is to be presented.
Each employee travels by one of four modes of transport - Metro train (M), Local train (L), office bus (B) and own vehicle (V)
Also, the employees are classified as males and females as well as technical or non-technical.
Hence, the entire classification can be as shown below.
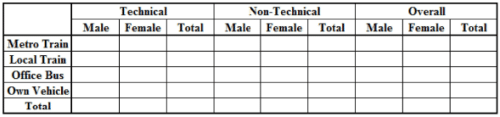
Denote employees by acronyms
i.e. Male = M, Female = F, Technical = T and Non-Technical = N
Classify each type of employee as gender-employee-type-(mode of transport)
e.g. a male technical employee travelling by local train or Metro train is MT(L) or MT(M) respectively and a female non-technical employee travelling by office bus is FN(B), and so on. Similarly, male technical employees are MT and total female employees travelling by Metro train are F(M) and so on.
Now, total employees = 2100 such that males and females are in the ratio 19 : 16
Number of males = (19/35) * 2100 = 1140 and number of females = 2100- 1140 = 960
Some information is directly given.
Of all the male employees who use the office bus, 123 are non-technical staff i.e. MN(B) = 123
Also, FN(M) = 136
Fill up the data obtained so far in the table.
Each employee travels by one of four modes of transport - Metro train (M), Local train (L), office bus (B) and own vehicle (V)
Also, the employees are classified as males and females as well as technical or non-technical.
Hence, the entire classification can be as shown below.
Denote employees by acronyms
i.e. Male = M, Female = F, Technical = T and Non-Technical = N
Classify each type of employee as gender-employee-type-(mode of transport)
e.g. a male technical employee travelling by local train or Metro train is MT(L) or MT(M) respectively and a female non-technical employee travelling by office bus is FN(B), and so on. Similarly, male technical employees are MT and total female employees travelling by Metro train are F(M) and so on.
Now, total employees = 2100 such that males and females are in the ratio 19 : 16
Number of males = (19/35) * 2100 = 1140 and number of females = 2100- 1140 = 960
Some information is directly given.
Of all the male employees who use the office bus, 123 are non-technical staff i.e. MN(B) = 123
Also, FN(M) = 136
Fill up the data obtained so far in the table.
Now, consider the direct information given for each type of vehicle.
Own Vehicle (V)
14% of employees use their own vehicle.
(V) = 0.14x2100 = 294
The ratio of technical to non-technical staff using their own vehicle is 2 :1 T(V) = (2/3) x 294 = 196 and N(V) = 294 - 196 = 98
Now, FT(V) = (1/3) x MT(V) and FT(V) = MN(V)
Now FT(V) + MT(V) = T(V)
FT(V) + 3FT(V) = 196
FT(V) = 49
MT(V) = 3 x 49 = 197 and MN(V) = 49 Now, MN(V) + FN(V) = N(V) = 98
FN(V) = 98 - 49 = 49
After the number of people using their own vehicle is removed, one-third of the remaining employees use the Metro trains.
(M) = (2100- 294)/3 = 602
Also (L) = 3(B)
(L) + (B) = 2100 - [(M) + (V)]
(L) + (B) = 2100 - 602 - 294 = 1204
Solving the two equations for (L) and (B), (B) = 301 and (L) = 903
Consider Local Train (L)
FN(L) = 20% of F and FN(L) = 80% of FT(L)
FN(L) = 0.2 x 960 = 192 and FT(L) = 192/0.8 = 240
F(L) = FN(L) + FT(L) = 192 + 240 = 432
M(L) = (L) - F(L) = 903 - 432 = 471
M(L) = MT(L) + MN(L) = 471
Also, MT(L) - MN(L) = 11
Solving these two equations, MT(L) = 241 and MN(L) = 230
T(L) = MT(L) + FT(L) = 241 + 240 = 441 and N(L) = MN(L) + FN(L) = 230 + 192 = 422
Hence, the table becomes:
Now consider Office Bus (B)
MN(B) = 123
FN(B) = (1/7) x (B) and M T (B ): FT(B) = 5 : 4
FN(B) = 301/7 = 43
N(B) = MN(B) + FN(B) = 123 + 43 = 166
T(B) = (B) - N(B) = 301 - 166 = 135
T(B) = MT(B) + FT(B) = 135 and M T (B ): FT(B) = 5 : 4
Solving these two equations, MT(B) = 75 and FT(B) = 60
M(B) = MT(B) + MN(B) = 75 + 123 = 198 and F(B) = 301 - 198 = 103
Now, MT + MN = M = 1140
and MN - MT = 4
MN = 572 and MT = 568
Thus, the table becomes:
Now, observe that the remaining values can be directly filled by addition or subtraction in respective rows or columns.
Hence, the final table is:
Male technical staff that travel by trains = MT(M) + MT(L) = 105 + 241 = 346 Female non-technical staff that do not travel by Local trains = FN(M) + FN(B) + FN(V) = 136 + 43 + 49 = 228
Required difference = 346 - 228 = 118 Hence, option 2.
Most Upvoted Answer
Group QuestionAnswer the following question based on the information g...
Analysis:
- Total employees: 2100
- Male to female ratio: 19:16
- Modes of transport: Metro trains, Local trains, own vehicles, office bus
- Staff classification: Technical, Non-technical
Males and Females Traveling by Local Trains:
- Females using Local trains: 0.2 * Total Female Staff = 0.2 * 16/35 * 2100 = 192
- Males using Local trains: 3 * Office Bus Users = 3 * 123 = 369
Males and Females Traveling by Own Vehicles:
- Females using own vehicles: 1/3 * Males using own vehicles = 1/3 * (2/3 * Total Own Vehicle Users - 192) = 1/3 * (2/3 * 0.14 * 2100 - 192) = 112
- Males using own vehicles: 2/3 * Total Own Vehicle Users - Females using own vehicles = 2/3 * 0.14 * 2100 - 112 = 308
Difference in Travel Mode:
- Males using Local trains: 369
- Male technical staff using Local trains: Males using Local trains - Male non-technical staff using Local trains = 369 - 123 = 246
- Female non-technical staff not using Local trains: Total Female Staff - Females using Local trains = 16/35 * 2100 - 192 = 368
- Difference: Male technical staff using Local trains - Female non-technical staff not using Local trains = 246 - 368 = -122 (rounded to -118)
Therefore, the difference between the number of male technical staff who travel by Local trains and the number of female non-technical staff who do not travel by Local trains is 118.
- Total employees: 2100
- Male to female ratio: 19:16
- Modes of transport: Metro trains, Local trains, own vehicles, office bus
- Staff classification: Technical, Non-technical
Males and Females Traveling by Local Trains:
- Females using Local trains: 0.2 * Total Female Staff = 0.2 * 16/35 * 2100 = 192
- Males using Local trains: 3 * Office Bus Users = 3 * 123 = 369
Males and Females Traveling by Own Vehicles:
- Females using own vehicles: 1/3 * Males using own vehicles = 1/3 * (2/3 * Total Own Vehicle Users - 192) = 1/3 * (2/3 * 0.14 * 2100 - 192) = 112
- Males using own vehicles: 2/3 * Total Own Vehicle Users - Females using own vehicles = 2/3 * 0.14 * 2100 - 112 = 308
Difference in Travel Mode:
- Males using Local trains: 369
- Male technical staff using Local trains: Males using Local trains - Male non-technical staff using Local trains = 369 - 123 = 246
- Female non-technical staff not using Local trains: Total Female Staff - Females using Local trains = 16/35 * 2100 - 192 = 368
- Difference: Male technical staff using Local trains - Female non-technical staff not using Local trains = 246 - 368 = -122 (rounded to -118)
Therefore, the difference between the number of male technical staff who travel by Local trains and the number of female non-technical staff who do not travel by Local trains is 118.
Attention CAT Students!
To make sure you are not studying endlessly, EduRev has designed CAT study material, with Structured Courses, Videos, & Test Series. Plus get personalized analysis, doubt solving and improvement plans to achieve a great score in CAT.

|
Explore Courses for CAT exam
|

|
Group QuestionAnswer the following question based on the information given below.A company has 2100 employees in all with male and female employees being in the ratio 19:16. Employees who come to office from the eastern or western part of the city use either the Metro trains or Local trains. The office also provides a bus service for people who stay far away and some employees use their own vehicles to commute to work. All the employees are classified as technical or nontechnical staff. 14% of the total employees use their own vehicles, with the ratio of the technical to non-technical staff in this group being 2 : 1. Of the remaining employees, one-third travel by Metro trains. The number of females who use their own vehicles and are technical staff is one-third of the number of males who are technical staff and use their own vehicles; as well as equal to the number of males who are non-technical staff and use their own vehicles. 20% of the total female staff is non-technical and uses the Local trains, which is equal to 80% of the female staff that is technical and uses Local trains. Of all the male employees who prefer to use the office bus, 123 are non-technical staff. The count of nontechnical male staff exceeds the technical male staff by four. The number of employees that use Local trains is three times the number of employees who use the office bus. One-seventh of the office bus users are non-technical female staff.The ratio of males to females who are technical staff and use office bus is 5 : 4.The number of male technical staff who use Local trains exceeds the male nontechnical staff using the same mode of transport by 11. 136 non-technical female staff use the Metro trains.Q.What is the difference between the number of male technical staff who travel bytrains andnumber of female non-technical staff who do not travel byLocal trains?a)93b)118c)202d)Data inadequateCorrect answer is option 'B'. Can you explain this answer?
Question Description
Group QuestionAnswer the following question based on the information given below.A company has 2100 employees in all with male and female employees being in the ratio 19:16. Employees who come to office from the eastern or western part of the city use either the Metro trains or Local trains. The office also provides a bus service for people who stay far away and some employees use their own vehicles to commute to work. All the employees are classified as technical or nontechnical staff. 14% of the total employees use their own vehicles, with the ratio of the technical to non-technical staff in this group being 2 : 1. Of the remaining employees, one-third travel by Metro trains. The number of females who use their own vehicles and are technical staff is one-third of the number of males who are technical staff and use their own vehicles; as well as equal to the number of males who are non-technical staff and use their own vehicles. 20% of the total female staff is non-technical and uses the Local trains, which is equal to 80% of the female staff that is technical and uses Local trains. Of all the male employees who prefer to use the office bus, 123 are non-technical staff. The count of nontechnical male staff exceeds the technical male staff by four. The number of employees that use Local trains is three times the number of employees who use the office bus. One-seventh of the office bus users are non-technical female staff.The ratio of males to females who are technical staff and use office bus is 5 : 4.The number of male technical staff who use Local trains exceeds the male nontechnical staff using the same mode of transport by 11. 136 non-technical female staff use the Metro trains.Q.What is the difference between the number of male technical staff who travel bytrains andnumber of female non-technical staff who do not travel byLocal trains?a)93b)118c)202d)Data inadequateCorrect answer is option 'B'. Can you explain this answer? for CAT 2024 is part of CAT preparation. The Question and answers have been prepared according to the CAT exam syllabus. Information about Group QuestionAnswer the following question based on the information given below.A company has 2100 employees in all with male and female employees being in the ratio 19:16. Employees who come to office from the eastern or western part of the city use either the Metro trains or Local trains. The office also provides a bus service for people who stay far away and some employees use their own vehicles to commute to work. All the employees are classified as technical or nontechnical staff. 14% of the total employees use their own vehicles, with the ratio of the technical to non-technical staff in this group being 2 : 1. Of the remaining employees, one-third travel by Metro trains. The number of females who use their own vehicles and are technical staff is one-third of the number of males who are technical staff and use their own vehicles; as well as equal to the number of males who are non-technical staff and use their own vehicles. 20% of the total female staff is non-technical and uses the Local trains, which is equal to 80% of the female staff that is technical and uses Local trains. Of all the male employees who prefer to use the office bus, 123 are non-technical staff. The count of nontechnical male staff exceeds the technical male staff by four. The number of employees that use Local trains is three times the number of employees who use the office bus. One-seventh of the office bus users are non-technical female staff.The ratio of males to females who are technical staff and use office bus is 5 : 4.The number of male technical staff who use Local trains exceeds the male nontechnical staff using the same mode of transport by 11. 136 non-technical female staff use the Metro trains.Q.What is the difference between the number of male technical staff who travel bytrains andnumber of female non-technical staff who do not travel byLocal trains?a)93b)118c)202d)Data inadequateCorrect answer is option 'B'. Can you explain this answer? covers all topics & solutions for CAT 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for Group QuestionAnswer the following question based on the information given below.A company has 2100 employees in all with male and female employees being in the ratio 19:16. Employees who come to office from the eastern or western part of the city use either the Metro trains or Local trains. The office also provides a bus service for people who stay far away and some employees use their own vehicles to commute to work. All the employees are classified as technical or nontechnical staff. 14% of the total employees use their own vehicles, with the ratio of the technical to non-technical staff in this group being 2 : 1. Of the remaining employees, one-third travel by Metro trains. The number of females who use their own vehicles and are technical staff is one-third of the number of males who are technical staff and use their own vehicles; as well as equal to the number of males who are non-technical staff and use their own vehicles. 20% of the total female staff is non-technical and uses the Local trains, which is equal to 80% of the female staff that is technical and uses Local trains. Of all the male employees who prefer to use the office bus, 123 are non-technical staff. The count of nontechnical male staff exceeds the technical male staff by four. The number of employees that use Local trains is three times the number of employees who use the office bus. One-seventh of the office bus users are non-technical female staff.The ratio of males to females who are technical staff and use office bus is 5 : 4.The number of male technical staff who use Local trains exceeds the male nontechnical staff using the same mode of transport by 11. 136 non-technical female staff use the Metro trains.Q.What is the difference between the number of male technical staff who travel bytrains andnumber of female non-technical staff who do not travel byLocal trains?a)93b)118c)202d)Data inadequateCorrect answer is option 'B'. Can you explain this answer?.
Group QuestionAnswer the following question based on the information given below.A company has 2100 employees in all with male and female employees being in the ratio 19:16. Employees who come to office from the eastern or western part of the city use either the Metro trains or Local trains. The office also provides a bus service for people who stay far away and some employees use their own vehicles to commute to work. All the employees are classified as technical or nontechnical staff. 14% of the total employees use their own vehicles, with the ratio of the technical to non-technical staff in this group being 2 : 1. Of the remaining employees, one-third travel by Metro trains. The number of females who use their own vehicles and are technical staff is one-third of the number of males who are technical staff and use their own vehicles; as well as equal to the number of males who are non-technical staff and use their own vehicles. 20% of the total female staff is non-technical and uses the Local trains, which is equal to 80% of the female staff that is technical and uses Local trains. Of all the male employees who prefer to use the office bus, 123 are non-technical staff. The count of nontechnical male staff exceeds the technical male staff by four. The number of employees that use Local trains is three times the number of employees who use the office bus. One-seventh of the office bus users are non-technical female staff.The ratio of males to females who are technical staff and use office bus is 5 : 4.The number of male technical staff who use Local trains exceeds the male nontechnical staff using the same mode of transport by 11. 136 non-technical female staff use the Metro trains.Q.What is the difference between the number of male technical staff who travel bytrains andnumber of female non-technical staff who do not travel byLocal trains?a)93b)118c)202d)Data inadequateCorrect answer is option 'B'. Can you explain this answer? for CAT 2024 is part of CAT preparation. The Question and answers have been prepared according to the CAT exam syllabus. Information about Group QuestionAnswer the following question based on the information given below.A company has 2100 employees in all with male and female employees being in the ratio 19:16. Employees who come to office from the eastern or western part of the city use either the Metro trains or Local trains. The office also provides a bus service for people who stay far away and some employees use their own vehicles to commute to work. All the employees are classified as technical or nontechnical staff. 14% of the total employees use their own vehicles, with the ratio of the technical to non-technical staff in this group being 2 : 1. Of the remaining employees, one-third travel by Metro trains. The number of females who use their own vehicles and are technical staff is one-third of the number of males who are technical staff and use their own vehicles; as well as equal to the number of males who are non-technical staff and use their own vehicles. 20% of the total female staff is non-technical and uses the Local trains, which is equal to 80% of the female staff that is technical and uses Local trains. Of all the male employees who prefer to use the office bus, 123 are non-technical staff. The count of nontechnical male staff exceeds the technical male staff by four. The number of employees that use Local trains is three times the number of employees who use the office bus. One-seventh of the office bus users are non-technical female staff.The ratio of males to females who are technical staff and use office bus is 5 : 4.The number of male technical staff who use Local trains exceeds the male nontechnical staff using the same mode of transport by 11. 136 non-technical female staff use the Metro trains.Q.What is the difference between the number of male technical staff who travel bytrains andnumber of female non-technical staff who do not travel byLocal trains?a)93b)118c)202d)Data inadequateCorrect answer is option 'B'. Can you explain this answer? covers all topics & solutions for CAT 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for Group QuestionAnswer the following question based on the information given below.A company has 2100 employees in all with male and female employees being in the ratio 19:16. Employees who come to office from the eastern or western part of the city use either the Metro trains or Local trains. The office also provides a bus service for people who stay far away and some employees use their own vehicles to commute to work. All the employees are classified as technical or nontechnical staff. 14% of the total employees use their own vehicles, with the ratio of the technical to non-technical staff in this group being 2 : 1. Of the remaining employees, one-third travel by Metro trains. The number of females who use their own vehicles and are technical staff is one-third of the number of males who are technical staff and use their own vehicles; as well as equal to the number of males who are non-technical staff and use their own vehicles. 20% of the total female staff is non-technical and uses the Local trains, which is equal to 80% of the female staff that is technical and uses Local trains. Of all the male employees who prefer to use the office bus, 123 are non-technical staff. The count of nontechnical male staff exceeds the technical male staff by four. The number of employees that use Local trains is three times the number of employees who use the office bus. One-seventh of the office bus users are non-technical female staff.The ratio of males to females who are technical staff and use office bus is 5 : 4.The number of male technical staff who use Local trains exceeds the male nontechnical staff using the same mode of transport by 11. 136 non-technical female staff use the Metro trains.Q.What is the difference between the number of male technical staff who travel bytrains andnumber of female non-technical staff who do not travel byLocal trains?a)93b)118c)202d)Data inadequateCorrect answer is option 'B'. Can you explain this answer?.
Solutions for Group QuestionAnswer the following question based on the information given below.A company has 2100 employees in all with male and female employees being in the ratio 19:16. Employees who come to office from the eastern or western part of the city use either the Metro trains or Local trains. The office also provides a bus service for people who stay far away and some employees use their own vehicles to commute to work. All the employees are classified as technical or nontechnical staff. 14% of the total employees use their own vehicles, with the ratio of the technical to non-technical staff in this group being 2 : 1. Of the remaining employees, one-third travel by Metro trains. The number of females who use their own vehicles and are technical staff is one-third of the number of males who are technical staff and use their own vehicles; as well as equal to the number of males who are non-technical staff and use their own vehicles. 20% of the total female staff is non-technical and uses the Local trains, which is equal to 80% of the female staff that is technical and uses Local trains. Of all the male employees who prefer to use the office bus, 123 are non-technical staff. The count of nontechnical male staff exceeds the technical male staff by four. The number of employees that use Local trains is three times the number of employees who use the office bus. One-seventh of the office bus users are non-technical female staff.The ratio of males to females who are technical staff and use office bus is 5 : 4.The number of male technical staff who use Local trains exceeds the male nontechnical staff using the same mode of transport by 11. 136 non-technical female staff use the Metro trains.Q.What is the difference between the number of male technical staff who travel bytrains andnumber of female non-technical staff who do not travel byLocal trains?a)93b)118c)202d)Data inadequateCorrect answer is option 'B'. Can you explain this answer? in English & in Hindi are available as part of our courses for CAT.
Download more important topics, notes, lectures and mock test series for CAT Exam by signing up for free.
Here you can find the meaning of Group QuestionAnswer the following question based on the information given below.A company has 2100 employees in all with male and female employees being in the ratio 19:16. Employees who come to office from the eastern or western part of the city use either the Metro trains or Local trains. The office also provides a bus service for people who stay far away and some employees use their own vehicles to commute to work. All the employees are classified as technical or nontechnical staff. 14% of the total employees use their own vehicles, with the ratio of the technical to non-technical staff in this group being 2 : 1. Of the remaining employees, one-third travel by Metro trains. The number of females who use their own vehicles and are technical staff is one-third of the number of males who are technical staff and use their own vehicles; as well as equal to the number of males who are non-technical staff and use their own vehicles. 20% of the total female staff is non-technical and uses the Local trains, which is equal to 80% of the female staff that is technical and uses Local trains. Of all the male employees who prefer to use the office bus, 123 are non-technical staff. The count of nontechnical male staff exceeds the technical male staff by four. The number of employees that use Local trains is three times the number of employees who use the office bus. One-seventh of the office bus users are non-technical female staff.The ratio of males to females who are technical staff and use office bus is 5 : 4.The number of male technical staff who use Local trains exceeds the male nontechnical staff using the same mode of transport by 11. 136 non-technical female staff use the Metro trains.Q.What is the difference between the number of male technical staff who travel bytrains andnumber of female non-technical staff who do not travel byLocal trains?a)93b)118c)202d)Data inadequateCorrect answer is option 'B'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
Group QuestionAnswer the following question based on the information given below.A company has 2100 employees in all with male and female employees being in the ratio 19:16. Employees who come to office from the eastern or western part of the city use either the Metro trains or Local trains. The office also provides a bus service for people who stay far away and some employees use their own vehicles to commute to work. All the employees are classified as technical or nontechnical staff. 14% of the total employees use their own vehicles, with the ratio of the technical to non-technical staff in this group being 2 : 1. Of the remaining employees, one-third travel by Metro trains. The number of females who use their own vehicles and are technical staff is one-third of the number of males who are technical staff and use their own vehicles; as well as equal to the number of males who are non-technical staff and use their own vehicles. 20% of the total female staff is non-technical and uses the Local trains, which is equal to 80% of the female staff that is technical and uses Local trains. Of all the male employees who prefer to use the office bus, 123 are non-technical staff. The count of nontechnical male staff exceeds the technical male staff by four. The number of employees that use Local trains is three times the number of employees who use the office bus. One-seventh of the office bus users are non-technical female staff.The ratio of males to females who are technical staff and use office bus is 5 : 4.The number of male technical staff who use Local trains exceeds the male nontechnical staff using the same mode of transport by 11. 136 non-technical female staff use the Metro trains.Q.What is the difference between the number of male technical staff who travel bytrains andnumber of female non-technical staff who do not travel byLocal trains?a)93b)118c)202d)Data inadequateCorrect answer is option 'B'. Can you explain this answer?, a detailed solution for Group QuestionAnswer the following question based on the information given below.A company has 2100 employees in all with male and female employees being in the ratio 19:16. Employees who come to office from the eastern or western part of the city use either the Metro trains or Local trains. The office also provides a bus service for people who stay far away and some employees use their own vehicles to commute to work. All the employees are classified as technical or nontechnical staff. 14% of the total employees use their own vehicles, with the ratio of the technical to non-technical staff in this group being 2 : 1. Of the remaining employees, one-third travel by Metro trains. The number of females who use their own vehicles and are technical staff is one-third of the number of males who are technical staff and use their own vehicles; as well as equal to the number of males who are non-technical staff and use their own vehicles. 20% of the total female staff is non-technical and uses the Local trains, which is equal to 80% of the female staff that is technical and uses Local trains. Of all the male employees who prefer to use the office bus, 123 are non-technical staff. The count of nontechnical male staff exceeds the technical male staff by four. The number of employees that use Local trains is three times the number of employees who use the office bus. One-seventh of the office bus users are non-technical female staff.The ratio of males to females who are technical staff and use office bus is 5 : 4.The number of male technical staff who use Local trains exceeds the male nontechnical staff using the same mode of transport by 11. 136 non-technical female staff use the Metro trains.Q.What is the difference between the number of male technical staff who travel bytrains andnumber of female non-technical staff who do not travel byLocal trains?a)93b)118c)202d)Data inadequateCorrect answer is option 'B'. Can you explain this answer? has been provided alongside types of Group QuestionAnswer the following question based on the information given below.A company has 2100 employees in all with male and female employees being in the ratio 19:16. Employees who come to office from the eastern or western part of the city use either the Metro trains or Local trains. The office also provides a bus service for people who stay far away and some employees use their own vehicles to commute to work. All the employees are classified as technical or nontechnical staff. 14% of the total employees use their own vehicles, with the ratio of the technical to non-technical staff in this group being 2 : 1. Of the remaining employees, one-third travel by Metro trains. The number of females who use their own vehicles and are technical staff is one-third of the number of males who are technical staff and use their own vehicles; as well as equal to the number of males who are non-technical staff and use their own vehicles. 20% of the total female staff is non-technical and uses the Local trains, which is equal to 80% of the female staff that is technical and uses Local trains. Of all the male employees who prefer to use the office bus, 123 are non-technical staff. The count of nontechnical male staff exceeds the technical male staff by four. The number of employees that use Local trains is three times the number of employees who use the office bus. One-seventh of the office bus users are non-technical female staff.The ratio of males to females who are technical staff and use office bus is 5 : 4.The number of male technical staff who use Local trains exceeds the male nontechnical staff using the same mode of transport by 11. 136 non-technical female staff use the Metro trains.Q.What is the difference between the number of male technical staff who travel bytrains andnumber of female non-technical staff who do not travel byLocal trains?a)93b)118c)202d)Data inadequateCorrect answer is option 'B'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice Group QuestionAnswer the following question based on the information given below.A company has 2100 employees in all with male and female employees being in the ratio 19:16. Employees who come to office from the eastern or western part of the city use either the Metro trains or Local trains. The office also provides a bus service for people who stay far away and some employees use their own vehicles to commute to work. All the employees are classified as technical or nontechnical staff. 14% of the total employees use their own vehicles, with the ratio of the technical to non-technical staff in this group being 2 : 1. Of the remaining employees, one-third travel by Metro trains. The number of females who use their own vehicles and are technical staff is one-third of the number of males who are technical staff and use their own vehicles; as well as equal to the number of males who are non-technical staff and use their own vehicles. 20% of the total female staff is non-technical and uses the Local trains, which is equal to 80% of the female staff that is technical and uses Local trains. Of all the male employees who prefer to use the office bus, 123 are non-technical staff. The count of nontechnical male staff exceeds the technical male staff by four. The number of employees that use Local trains is three times the number of employees who use the office bus. One-seventh of the office bus users are non-technical female staff.The ratio of males to females who are technical staff and use office bus is 5 : 4.The number of male technical staff who use Local trains exceeds the male nontechnical staff using the same mode of transport by 11. 136 non-technical female staff use the Metro trains.Q.What is the difference between the number of male technical staff who travel bytrains andnumber of female non-technical staff who do not travel byLocal trains?a)93b)118c)202d)Data inadequateCorrect answer is option 'B'. Can you explain this answer? tests, examples and also practice CAT tests.

|
Explore Courses for CAT exam
|

|
Suggested Free Tests
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.






















