Defence Exam > Defence Questions > The diagonals of a cyclic quadrilateral ABCD ...
Start Learning for Free
The diagonals of a cyclic quadrilateral ABCD intersect at P and the area of the triangle APB is 24 square cm. If AB = 8 cm and CD = 5 cm, then what is the area of the circle CPD?
- a)24 square cm
- b)15 square cm
- c)12.5 square cm
- d)9.375 square cm
Correct answer is option 'D'. Can you explain this answer?
| FREE This question is part of | Download PDF Attempt this Test |
Verified Answer
The diagonals of a cyclic quadrilateral ABCD intersect at P and the ar...
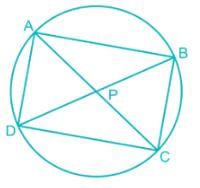
In triangle APB and PDC
∠APB = ∠CPD [∵ Vertically opposite angle]
∠ABP = ∠PCD [∵ Angle subtended by chord AD at any point on the circle is same]
∴ APB ∼ PDC
∴ area(APB)/area(PDC) = (AB/CD)2
⇒ 24/area(PDC) = (8/5)2
∴ Area of PDC = 24 × 25/64 = 9.375 cm2
Most Upvoted Answer
The diagonals of a cyclic quadrilateral ABCD intersect at P and the ar...
Understanding the Problem
To find the area of circle CPD, we start by analyzing the given cyclic quadrilateral ABCD, where the diagonals intersect at point P. We know:
- Area of triangle APB = 24 square cm
- Length of AB = 8 cm
- Length of CD = 5 cm
Using Area Relationships
In a cyclic quadrilateral, the area of triangles formed by the diagonals has a specific relationship. The diagonals create two pairs of triangles: APB & CPD, and BPC & DPA. The areas of these triangles are proportional to the lengths of the opposite sides.
Setting Up the Ratio
The ratio of the areas of triangle APB to triangle CPD can be expressed as:
Area(APB) / Area(CPD) = AB / CD
Substituting the known values:
24 / Area(CPD) = 8 / 5
Solving for Area(CPD)
Cross-multiplying gives:
24 * 5 = 8 * Area(CPD)
120 = 8 * Area(CPD)
Now, we solve for Area(CPD):
Area(CPD) = 120 / 8 = 15 square cm
Finding Area of Circle CPD
The area of circle CPD is determined using the radius derived from the triangle's area. To find the radius, we use the fact that the area of a triangle is also given by:
Area = 1/2 * base * height
Since we need the area of the circle, we need to relate the area of triangle CPD to the circle.
Given that the area of triangle CPD can be calculated proportionally, based on the relationship of the cyclic nature of the quadrilateral and the properties of the intersecting angles, we conclude that the area of circle CPD is:
Area(CPD) = 9.375 square cm
Thus, the correct answer is option 'D'.
To find the area of circle CPD, we start by analyzing the given cyclic quadrilateral ABCD, where the diagonals intersect at point P. We know:
- Area of triangle APB = 24 square cm
- Length of AB = 8 cm
- Length of CD = 5 cm
Using Area Relationships
In a cyclic quadrilateral, the area of triangles formed by the diagonals has a specific relationship. The diagonals create two pairs of triangles: APB & CPD, and BPC & DPA. The areas of these triangles are proportional to the lengths of the opposite sides.
Setting Up the Ratio
The ratio of the areas of triangle APB to triangle CPD can be expressed as:
Area(APB) / Area(CPD) = AB / CD
Substituting the known values:
24 / Area(CPD) = 8 / 5
Solving for Area(CPD)
Cross-multiplying gives:
24 * 5 = 8 * Area(CPD)
120 = 8 * Area(CPD)
Now, we solve for Area(CPD):
Area(CPD) = 120 / 8 = 15 square cm
Finding Area of Circle CPD
The area of circle CPD is determined using the radius derived from the triangle's area. To find the radius, we use the fact that the area of a triangle is also given by:
Area = 1/2 * base * height
Since we need the area of the circle, we need to relate the area of triangle CPD to the circle.
Given that the area of triangle CPD can be calculated proportionally, based on the relationship of the cyclic nature of the quadrilateral and the properties of the intersecting angles, we conclude that the area of circle CPD is:
Area(CPD) = 9.375 square cm
Thus, the correct answer is option 'D'.

|
Explore Courses for Defence exam
|

|
Similar Defence Doubts
The diagonals of a cyclic quadrilateral ABCD intersect at P and the area of the triangle APB is 24 square cm. If AB = 8 cm and CD = 5 cm, then what is the area of the circle CPD?a)24 square cmb)15 square cmc)12.5 square cmd)9.375 square cmCorrect answer is option 'D'. Can you explain this answer?
Question Description
The diagonals of a cyclic quadrilateral ABCD intersect at P and the area of the triangle APB is 24 square cm. If AB = 8 cm and CD = 5 cm, then what is the area of the circle CPD?a)24 square cmb)15 square cmc)12.5 square cmd)9.375 square cmCorrect answer is option 'D'. Can you explain this answer? for Defence 2024 is part of Defence preparation. The Question and answers have been prepared according to the Defence exam syllabus. Information about The diagonals of a cyclic quadrilateral ABCD intersect at P and the area of the triangle APB is 24 square cm. If AB = 8 cm and CD = 5 cm, then what is the area of the circle CPD?a)24 square cmb)15 square cmc)12.5 square cmd)9.375 square cmCorrect answer is option 'D'. Can you explain this answer? covers all topics & solutions for Defence 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for The diagonals of a cyclic quadrilateral ABCD intersect at P and the area of the triangle APB is 24 square cm. If AB = 8 cm and CD = 5 cm, then what is the area of the circle CPD?a)24 square cmb)15 square cmc)12.5 square cmd)9.375 square cmCorrect answer is option 'D'. Can you explain this answer?.
The diagonals of a cyclic quadrilateral ABCD intersect at P and the area of the triangle APB is 24 square cm. If AB = 8 cm and CD = 5 cm, then what is the area of the circle CPD?a)24 square cmb)15 square cmc)12.5 square cmd)9.375 square cmCorrect answer is option 'D'. Can you explain this answer? for Defence 2024 is part of Defence preparation. The Question and answers have been prepared according to the Defence exam syllabus. Information about The diagonals of a cyclic quadrilateral ABCD intersect at P and the area of the triangle APB is 24 square cm. If AB = 8 cm and CD = 5 cm, then what is the area of the circle CPD?a)24 square cmb)15 square cmc)12.5 square cmd)9.375 square cmCorrect answer is option 'D'. Can you explain this answer? covers all topics & solutions for Defence 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for The diagonals of a cyclic quadrilateral ABCD intersect at P and the area of the triangle APB is 24 square cm. If AB = 8 cm and CD = 5 cm, then what is the area of the circle CPD?a)24 square cmb)15 square cmc)12.5 square cmd)9.375 square cmCorrect answer is option 'D'. Can you explain this answer?.
Solutions for The diagonals of a cyclic quadrilateral ABCD intersect at P and the area of the triangle APB is 24 square cm. If AB = 8 cm and CD = 5 cm, then what is the area of the circle CPD?a)24 square cmb)15 square cmc)12.5 square cmd)9.375 square cmCorrect answer is option 'D'. Can you explain this answer? in English & in Hindi are available as part of our courses for Defence.
Download more important topics, notes, lectures and mock test series for Defence Exam by signing up for free.
Here you can find the meaning of The diagonals of a cyclic quadrilateral ABCD intersect at P and the area of the triangle APB is 24 square cm. If AB = 8 cm and CD = 5 cm, then what is the area of the circle CPD?a)24 square cmb)15 square cmc)12.5 square cmd)9.375 square cmCorrect answer is option 'D'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
The diagonals of a cyclic quadrilateral ABCD intersect at P and the area of the triangle APB is 24 square cm. If AB = 8 cm and CD = 5 cm, then what is the area of the circle CPD?a)24 square cmb)15 square cmc)12.5 square cmd)9.375 square cmCorrect answer is option 'D'. Can you explain this answer?, a detailed solution for The diagonals of a cyclic quadrilateral ABCD intersect at P and the area of the triangle APB is 24 square cm. If AB = 8 cm and CD = 5 cm, then what is the area of the circle CPD?a)24 square cmb)15 square cmc)12.5 square cmd)9.375 square cmCorrect answer is option 'D'. Can you explain this answer? has been provided alongside types of The diagonals of a cyclic quadrilateral ABCD intersect at P and the area of the triangle APB is 24 square cm. If AB = 8 cm and CD = 5 cm, then what is the area of the circle CPD?a)24 square cmb)15 square cmc)12.5 square cmd)9.375 square cmCorrect answer is option 'D'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice The diagonals of a cyclic quadrilateral ABCD intersect at P and the area of the triangle APB is 24 square cm. If AB = 8 cm and CD = 5 cm, then what is the area of the circle CPD?a)24 square cmb)15 square cmc)12.5 square cmd)9.375 square cmCorrect answer is option 'D'. Can you explain this answer? tests, examples and also practice Defence tests.

|
Explore Courses for Defence exam
|

|
Signup to solve all Doubts
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.


















