Defence Exam > Defence Questions > The numbers 1, 5 and 25 can be three terms (n...
Start Learning for Free
The numbers 1, 5 and 25 can be three terms (not necessarily consecutive) of
- a)only one AP
- b)more than one but finite numbers of APs
- c)infinite number of APs
- d)finite number of GPs
Correct answer is option 'C'. Can you explain this answer?
| FREE This question is part of | Download PDF Attempt this Test |
Verified Answer
The numbers 1, 5 and 25 can be three terms (not necessarily consecutiv...
The numbers 1,5 and 25 can be three terms (not necessarily consecutive) of one or many numbers of Arithmetic and Geometric Progressions.
To check the Arithmetic Progression: Let us assume that given number series 1, 5 and 25 are Ith, Jth and Qth terms in the AP series whose distance is equal to d.
Therefore,
To check the Arithmetic Progression: Let us assume that given number series 1, 5 and 25 are Ith, Jth and Qth terms in the AP series whose distance is equal to d.
Therefore,
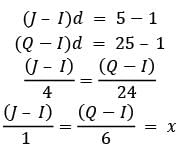
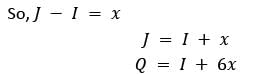
Here x is a natural number.
So, the given three numbers can be terms in one or many numbers of
Arithmetic Progressions.
Most Upvoted Answer
The numbers 1, 5 and 25 can be three terms (not necessarily consecutiv...
Question Analysis:
The question asks us to determine which categories the numbers 1, 5, and 25 fall into. We need to consider whether these numbers can form an arithmetic progression (AP) or a geometric progression (GP), and if so, how many such progressions they can form.
Answer Explanation:
The numbers 1, 5, and 25 can form an infinite number of arithmetic progressions. We can see this by considering the common differences between the terms.
Arithmetic Progression:
An arithmetic progression is a sequence of numbers in which the difference between any two consecutive terms is always the same. In other words, if we subtract any term from the next term, we will always get the same value.
To determine if 1, 5, and 25 can form an arithmetic progression, we need to check if the differences between consecutive terms are the same.
- Difference between 5 and 1: 5 - 1 = 4
- Difference between 25 and 5: 25 - 5 = 20
The difference between consecutive terms is not the same. Therefore, the numbers 1, 5, and 25 cannot form an arithmetic progression on their own. However, if we consider the common differences between the terms and use them as the common differences for an arithmetic progression, we can see that an infinite number of arithmetic progressions can be formed.
Example of an Arithmetic Progression:
Let's take the common difference between consecutive terms as 4 (the difference between 5 and 1). Using this common difference, we can form an arithmetic progression as follows:
1, 5, 9, 13, 17, 21, ...
In this progression, the difference between any two consecutive terms is always 4. We can continue this progression indefinitely, creating an infinite number of arithmetic progressions using the numbers 1, 5, and 25. Therefore, the correct answer is option C: an infinite number of arithmetic progressions.
Conclusion:
The numbers 1, 5, and 25 can form an infinite number of arithmetic progressions. This is because the common differences between the terms can be used to create an infinite number of arithmetic progressions.
The question asks us to determine which categories the numbers 1, 5, and 25 fall into. We need to consider whether these numbers can form an arithmetic progression (AP) or a geometric progression (GP), and if so, how many such progressions they can form.
Answer Explanation:
The numbers 1, 5, and 25 can form an infinite number of arithmetic progressions. We can see this by considering the common differences between the terms.
Arithmetic Progression:
An arithmetic progression is a sequence of numbers in which the difference between any two consecutive terms is always the same. In other words, if we subtract any term from the next term, we will always get the same value.
To determine if 1, 5, and 25 can form an arithmetic progression, we need to check if the differences between consecutive terms are the same.
- Difference between 5 and 1: 5 - 1 = 4
- Difference between 25 and 5: 25 - 5 = 20
The difference between consecutive terms is not the same. Therefore, the numbers 1, 5, and 25 cannot form an arithmetic progression on their own. However, if we consider the common differences between the terms and use them as the common differences for an arithmetic progression, we can see that an infinite number of arithmetic progressions can be formed.
Example of an Arithmetic Progression:
Let's take the common difference between consecutive terms as 4 (the difference between 5 and 1). Using this common difference, we can form an arithmetic progression as follows:
1, 5, 9, 13, 17, 21, ...
In this progression, the difference between any two consecutive terms is always 4. We can continue this progression indefinitely, creating an infinite number of arithmetic progressions using the numbers 1, 5, and 25. Therefore, the correct answer is option C: an infinite number of arithmetic progressions.
Conclusion:
The numbers 1, 5, and 25 can form an infinite number of arithmetic progressions. This is because the common differences between the terms can be used to create an infinite number of arithmetic progressions.

|
Explore Courses for Defence exam
|

|
Similar Defence Doubts
The numbers 1, 5 and 25 can be three terms (not necessarily consecutive) ofa)only one APb)more than one but finite numbers of APsc)infinite number of APsd)finite number of GPsCorrect answer is option 'C'. Can you explain this answer?
Question Description
The numbers 1, 5 and 25 can be three terms (not necessarily consecutive) ofa)only one APb)more than one but finite numbers of APsc)infinite number of APsd)finite number of GPsCorrect answer is option 'C'. Can you explain this answer? for Defence 2024 is part of Defence preparation. The Question and answers have been prepared according to the Defence exam syllabus. Information about The numbers 1, 5 and 25 can be three terms (not necessarily consecutive) ofa)only one APb)more than one but finite numbers of APsc)infinite number of APsd)finite number of GPsCorrect answer is option 'C'. Can you explain this answer? covers all topics & solutions for Defence 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for The numbers 1, 5 and 25 can be three terms (not necessarily consecutive) ofa)only one APb)more than one but finite numbers of APsc)infinite number of APsd)finite number of GPsCorrect answer is option 'C'. Can you explain this answer?.
The numbers 1, 5 and 25 can be three terms (not necessarily consecutive) ofa)only one APb)more than one but finite numbers of APsc)infinite number of APsd)finite number of GPsCorrect answer is option 'C'. Can you explain this answer? for Defence 2024 is part of Defence preparation. The Question and answers have been prepared according to the Defence exam syllabus. Information about The numbers 1, 5 and 25 can be three terms (not necessarily consecutive) ofa)only one APb)more than one but finite numbers of APsc)infinite number of APsd)finite number of GPsCorrect answer is option 'C'. Can you explain this answer? covers all topics & solutions for Defence 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for The numbers 1, 5 and 25 can be three terms (not necessarily consecutive) ofa)only one APb)more than one but finite numbers of APsc)infinite number of APsd)finite number of GPsCorrect answer is option 'C'. Can you explain this answer?.
Solutions for The numbers 1, 5 and 25 can be three terms (not necessarily consecutive) ofa)only one APb)more than one but finite numbers of APsc)infinite number of APsd)finite number of GPsCorrect answer is option 'C'. Can you explain this answer? in English & in Hindi are available as part of our courses for Defence.
Download more important topics, notes, lectures and mock test series for Defence Exam by signing up for free.
Here you can find the meaning of The numbers 1, 5 and 25 can be three terms (not necessarily consecutive) ofa)only one APb)more than one but finite numbers of APsc)infinite number of APsd)finite number of GPsCorrect answer is option 'C'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
The numbers 1, 5 and 25 can be three terms (not necessarily consecutive) ofa)only one APb)more than one but finite numbers of APsc)infinite number of APsd)finite number of GPsCorrect answer is option 'C'. Can you explain this answer?, a detailed solution for The numbers 1, 5 and 25 can be three terms (not necessarily consecutive) ofa)only one APb)more than one but finite numbers of APsc)infinite number of APsd)finite number of GPsCorrect answer is option 'C'. Can you explain this answer? has been provided alongside types of The numbers 1, 5 and 25 can be three terms (not necessarily consecutive) ofa)only one APb)more than one but finite numbers of APsc)infinite number of APsd)finite number of GPsCorrect answer is option 'C'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice The numbers 1, 5 and 25 can be three terms (not necessarily consecutive) ofa)only one APb)more than one but finite numbers of APsc)infinite number of APsd)finite number of GPsCorrect answer is option 'C'. Can you explain this answer? tests, examples and also practice Defence tests.

|
Explore Courses for Defence exam
|

|
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.


















