Defence Exam > Defence Questions > The sum of the focal distances of a point on ...
Start Learning for Free
The sum of the focal distances of a point on an ellipse is constant and equal to the
- a)length of minor axis
- b)length of major axis
- c)length of latus rectum
- d)sum of the lengths of semi-major and semi-minor axes
Correct answer is option 'B'. Can you explain this answer?
| FREE This question is part of | Download PDF Attempt this Test |
Verified Answer
The sum of the focal distances of a point on an ellipse is constant an...
The sum of the focal distance of any point on an ellipse is constant and equal to the length of the major axis of the ellipse.
Let P (x, y) be any point on the ellipse
Let P (x, y) be any point on the ellipse
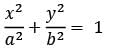
Let MPM' be the perpendicular through P on directrices ZK and Z'K'. Now by definition we get,

Hence, the sum of the focal distance of a point P 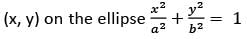 is constant and equal to the length of the major axis i.e., 2a of the ellipse.
is constant and equal to the length of the major axis i.e., 2a of the ellipse.
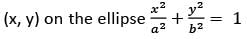 is constant and equal to the length of the major axis i.e., 2a of the ellipse.
is constant and equal to the length of the major axis i.e., 2a of the ellipse.Most Upvoted Answer
The sum of the focal distances of a point on an ellipse is constant an...
Explanation:
An ellipse is a closed curve formed by the intersection of a cone and a plane. It has two main axes - the major axis and the minor axis. The major axis is the longer axis and the minor axis is the shorter axis of the ellipse.
The focal points of an ellipse are two points on the major axis, denoted as F1 and F2. The sum of the distances of any point on the ellipse from these two focal points is always constant and equal to the length of the major axis.
Proof:
Let's consider an ellipse with semi-major axis 'a' and semi-minor axis 'b'. The distance between the center of the ellipse and each focal point is denoted as 'c'.
The sum of the distances of a point on the ellipse from the two focal points is:
S = PF1 + PF2
where PF1 is the distance from the point to F1 and PF2 is the distance from the point to F2.
Using the distance formula, we can calculate PF1 and PF2 as follows:
PF1 = sqrt((x-c)^2 + y^2)
PF2 = sqrt((x+c)^2 + y^2)
where (x, y) are the coordinates of the point on the ellipse.
Substituting the values of PF1 and PF2 into the equation for S:
S = sqrt((x-c)^2 + y^2) + sqrt((x+c)^2 + y^2)
To simplify this equation, we can square both sides:
S^2 = ((x-c)^2 + y^2) + 2(sqrt((x-c)^2 + y^2) * sqrt((x+c)^2 + y^2)) + ((x+c)^2 + y^2)
Simplifying further, we get:
S^2 = 2(x^2 + c^2 + y^2) + 2(sqrt((x-c)^2 + y^2) * sqrt((x+c)^2 + y^2))
Using the equation of the ellipse, which states that (x^2/a^2) + (y^2/b^2) = 1, we can substitute (x^2 + y^2) with a^2 - (a^2/b^2) * x^2:
S^2 = 2(a^2 - (a^2/b^2) * x^2 + c^2) + 2(sqrt((x-c)^2 + y^2) * sqrt((x+c)^2 + y^2))
Simplifying further, we get:
S^2 = 2(a^2 + c^2) - (2a^2/b^2) * x^2 + 2(sqrt((x-c)^2 + y^2) * sqrt((x+c)^2 + y^2))
Notice that the term (2a^2/b^2) * x^2 is independent of the point on the ellipse. This means that it remains constant for all points on the ellipse.
Therefore, the sum of the distances of any point on the ellipse from the two focal points is constant and equal to:
S^2 = 2(a^2 + c^2)
Since the length of the major axis is 2a, we can rewrite the equation as:
S
An ellipse is a closed curve formed by the intersection of a cone and a plane. It has two main axes - the major axis and the minor axis. The major axis is the longer axis and the minor axis is the shorter axis of the ellipse.
The focal points of an ellipse are two points on the major axis, denoted as F1 and F2. The sum of the distances of any point on the ellipse from these two focal points is always constant and equal to the length of the major axis.
Proof:
Let's consider an ellipse with semi-major axis 'a' and semi-minor axis 'b'. The distance between the center of the ellipse and each focal point is denoted as 'c'.
The sum of the distances of a point on the ellipse from the two focal points is:
S = PF1 + PF2
where PF1 is the distance from the point to F1 and PF2 is the distance from the point to F2.
Using the distance formula, we can calculate PF1 and PF2 as follows:
PF1 = sqrt((x-c)^2 + y^2)
PF2 = sqrt((x+c)^2 + y^2)
where (x, y) are the coordinates of the point on the ellipse.
Substituting the values of PF1 and PF2 into the equation for S:
S = sqrt((x-c)^2 + y^2) + sqrt((x+c)^2 + y^2)
To simplify this equation, we can square both sides:
S^2 = ((x-c)^2 + y^2) + 2(sqrt((x-c)^2 + y^2) * sqrt((x+c)^2 + y^2)) + ((x+c)^2 + y^2)
Simplifying further, we get:
S^2 = 2(x^2 + c^2 + y^2) + 2(sqrt((x-c)^2 + y^2) * sqrt((x+c)^2 + y^2))
Using the equation of the ellipse, which states that (x^2/a^2) + (y^2/b^2) = 1, we can substitute (x^2 + y^2) with a^2 - (a^2/b^2) * x^2:
S^2 = 2(a^2 - (a^2/b^2) * x^2 + c^2) + 2(sqrt((x-c)^2 + y^2) * sqrt((x+c)^2 + y^2))
Simplifying further, we get:
S^2 = 2(a^2 + c^2) - (2a^2/b^2) * x^2 + 2(sqrt((x-c)^2 + y^2) * sqrt((x+c)^2 + y^2))
Notice that the term (2a^2/b^2) * x^2 is independent of the point on the ellipse. This means that it remains constant for all points on the ellipse.
Therefore, the sum of the distances of any point on the ellipse from the two focal points is constant and equal to:
S^2 = 2(a^2 + c^2)
Since the length of the major axis is 2a, we can rewrite the equation as:
S

|
Explore Courses for Defence exam
|

|
The sum of the focal distances of a point on an ellipse is constant and equal to thea)length of minor axisb)length of major axisc)length of latus rectumd)sum of the lengths of semi-major and semi-minor axesCorrect answer is option 'B'. Can you explain this answer?
Question Description
The sum of the focal distances of a point on an ellipse is constant and equal to thea)length of minor axisb)length of major axisc)length of latus rectumd)sum of the lengths of semi-major and semi-minor axesCorrect answer is option 'B'. Can you explain this answer? for Defence 2024 is part of Defence preparation. The Question and answers have been prepared according to the Defence exam syllabus. Information about The sum of the focal distances of a point on an ellipse is constant and equal to thea)length of minor axisb)length of major axisc)length of latus rectumd)sum of the lengths of semi-major and semi-minor axesCorrect answer is option 'B'. Can you explain this answer? covers all topics & solutions for Defence 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for The sum of the focal distances of a point on an ellipse is constant and equal to thea)length of minor axisb)length of major axisc)length of latus rectumd)sum of the lengths of semi-major and semi-minor axesCorrect answer is option 'B'. Can you explain this answer?.
The sum of the focal distances of a point on an ellipse is constant and equal to thea)length of minor axisb)length of major axisc)length of latus rectumd)sum of the lengths of semi-major and semi-minor axesCorrect answer is option 'B'. Can you explain this answer? for Defence 2024 is part of Defence preparation. The Question and answers have been prepared according to the Defence exam syllabus. Information about The sum of the focal distances of a point on an ellipse is constant and equal to thea)length of minor axisb)length of major axisc)length of latus rectumd)sum of the lengths of semi-major and semi-minor axesCorrect answer is option 'B'. Can you explain this answer? covers all topics & solutions for Defence 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for The sum of the focal distances of a point on an ellipse is constant and equal to thea)length of minor axisb)length of major axisc)length of latus rectumd)sum of the lengths of semi-major and semi-minor axesCorrect answer is option 'B'. Can you explain this answer?.
Solutions for The sum of the focal distances of a point on an ellipse is constant and equal to thea)length of minor axisb)length of major axisc)length of latus rectumd)sum of the lengths of semi-major and semi-minor axesCorrect answer is option 'B'. Can you explain this answer? in English & in Hindi are available as part of our courses for Defence.
Download more important topics, notes, lectures and mock test series for Defence Exam by signing up for free.
Here you can find the meaning of The sum of the focal distances of a point on an ellipse is constant and equal to thea)length of minor axisb)length of major axisc)length of latus rectumd)sum of the lengths of semi-major and semi-minor axesCorrect answer is option 'B'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
The sum of the focal distances of a point on an ellipse is constant and equal to thea)length of minor axisb)length of major axisc)length of latus rectumd)sum of the lengths of semi-major and semi-minor axesCorrect answer is option 'B'. Can you explain this answer?, a detailed solution for The sum of the focal distances of a point on an ellipse is constant and equal to thea)length of minor axisb)length of major axisc)length of latus rectumd)sum of the lengths of semi-major and semi-minor axesCorrect answer is option 'B'. Can you explain this answer? has been provided alongside types of The sum of the focal distances of a point on an ellipse is constant and equal to thea)length of minor axisb)length of major axisc)length of latus rectumd)sum of the lengths of semi-major and semi-minor axesCorrect answer is option 'B'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice The sum of the focal distances of a point on an ellipse is constant and equal to thea)length of minor axisb)length of major axisc)length of latus rectumd)sum of the lengths of semi-major and semi-minor axesCorrect answer is option 'B'. Can you explain this answer? tests, examples and also practice Defence tests.

|
Explore Courses for Defence exam
|

|
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.


















