CAT Exam > CAT Questions > InstructionsFun Sports (FS) provides training...
Start Learning for Free
Instructions
Fun Sports (FS) provides training in three sports - Gilli-danda (G), Kho-Kho (K), and Ludo (L). Currently it has an enrollment of 39 students each of whom is enrolled in at least one of the three sports. The following details are known:
1. The number of students enrolled only in L is double the number of students enrolled in all the three sports.
2. There are a total of 17 students enrolled in G.
3. The number of students enrolled only in G is one less than the number of students enrolled only in L.
4. The number of students enrolled only in K is equal to the number of students who are enrolled in both K and L.
5. The maximum student enrollment is in L.
6. Ten students enrolled in G are also enrolled in at least one more sport.
Q. Due to academic pressure, students who were enrolled in all three sports were asked to withdraw from one of the three sports. After the withdrawal, the number of students enrolled in G was six less than the number of students enrolled in L, while the number of students enrolled in K went down by one. After the withdrawal, how many students were enrolled in both G and K?
Fun Sports (FS) provides training in three sports - Gilli-danda (G), Kho-Kho (K), and Ludo (L). Currently it has an enrollment of 39 students each of whom is enrolled in at least one of the three sports. The following details are known:
1. The number of students enrolled only in L is double the number of students enrolled in all the three sports.
2. There are a total of 17 students enrolled in G.
3. The number of students enrolled only in G is one less than the number of students enrolled only in L.
4. The number of students enrolled only in K is equal to the number of students who are enrolled in both K and L.
5. The maximum student enrollment is in L.
6. Ten students enrolled in G are also enrolled in at least one more sport.
Q. Due to academic pressure, students who were enrolled in all three sports were asked to withdraw from one of the three sports. After the withdrawal, the number of students enrolled in G was six less than the number of students enrolled in L, while the number of students enrolled in K went down by one. After the withdrawal, how many students were enrolled in both G and K?
Correct answer is '2'. Can you explain this answer?
Verified Answer
InstructionsFun Sports (FS) provides training in three sports - Gilli-...
Let 'x' be the number of students enrolled in all three sports. Then the number of students enrolled only in L = 2x It is given that there are a total of 17 students enrolled in G. Also, ten students enrolled in G are also enrolled in at least one more sport. Hence, the number of students enrolled in only G = 17 - 10 = 7
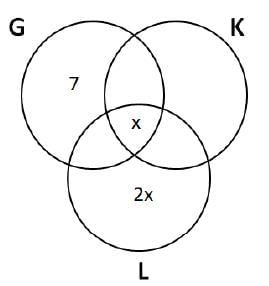
The number of students enrolled only in G is one less than the number of students enrolled only in L. Hence, the number of students enrolled only in L = 7+1
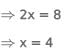
Let us assume that 'y' students are enrolled in K and L but not G. Then, the number of students enrolled only in K = y + 4
Let us assume that 'z' be the the number of students enrolled in G and K but not L. Then, the number of students enrolled G and L bot not K = 10 - 4 - z = 6 - z
It is given that a total of 39 students in the sports.
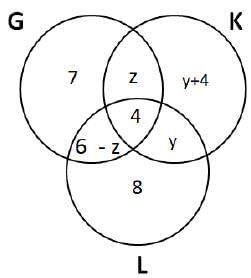
7 + z + 4 + 6 - z + 8 + y + y + 4 = 39
⇒ y = 5
Number of students enrolled in G = 17
Number of students enrolled in K = 9 + 4 + 5 + z = 18 + z
Number of students enrolled in L = 6 - z + 4 + 5 + 8 = 23 - z
It is given that the maximum student enrollment is in L.

Therefore, we can say that z can take three values = {0, 1, 2} Hence, the number of students enrolled in K = 18 + z = {18, 19, 20} It is given that after withdrawal the number of students enrolled in K went down by one. This one student must have left sports K. Hence we can say that the remaining 3 students must have left either G or L.
Before withdraw there were a total of 24 students were enrolled in exactly 1 sports, 11 students were enrolled in exactly 2 courses and 4 students were enrolled in all three courses.
The students which were enrolled in all three sports, withdrew from one of the sports. Hence, we can say that now the number of students who were enrolled in exactly 2 courses = 11 + 4 = 15.
It is given that the number of students enrolled in G was six less than the number of students enrolled in L. Let 'a' be the number of students who were enrolled in G and K but not L. Then, the number of students who were enrolled in L and K but not G = a + 5
Consequently, we can say that the number of students enrolled in G and L but not K = 15 - (2a + 5) = 10 - 2a
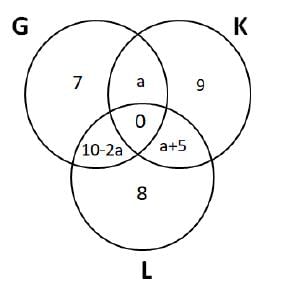
Number of students enrolled in this case = a + a+5 + 9 = 14 + 2a. We can see that '14+2a' is an even number. It is given that the number of students enrolled in K went down by one. Therefore, we can say that the number of students
enrolled in K earlier was an odd number.
Hence, the number of students enrolled in K = 18 + z = {18, 19, 20}
We can see that only '19' is an odd number. Hence, we can say that the number of students enrolled in K after withdrawal = 18
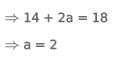
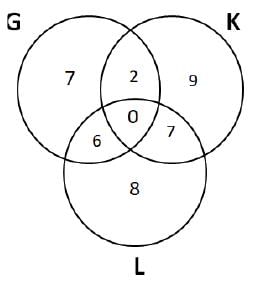
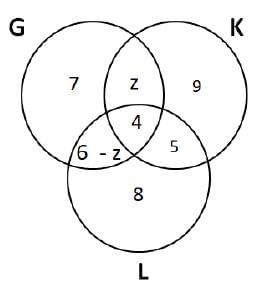
From the diagram we can see that the number of students enrolled in both G and K = 2.

The number of students enrolled only in G is one less than the number of students enrolled only in L. Hence, the number of students enrolled only in L = 7+1
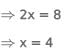
Let us assume that 'y' students are enrolled in K and L but not G. Then, the number of students enrolled only in K = y + 4
Let us assume that 'z' be the the number of students enrolled in G and K but not L. Then, the number of students enrolled G and L bot not K = 10 - 4 - z = 6 - z

It is given that a total of 39 students in the sports.
7 + z + 4 + 6 - z + 8 + y + y + 4 = 39
⇒ y = 5

Number of students enrolled in G = 17
Number of students enrolled in K = 9 + 4 + 5 + z = 18 + z
Number of students enrolled in L = 6 - z + 4 + 5 + 8 = 23 - z
It is given that the maximum student enrollment is in L.

Therefore, we can say that z can take three values = {0, 1, 2} Hence, the number of students enrolled in K = 18 + z = {18, 19, 20} It is given that after withdrawal the number of students enrolled in K went down by one. This one student must have left sports K. Hence we can say that the remaining 3 students must have left either G or L.
Before withdraw there were a total of 24 students were enrolled in exactly 1 sports, 11 students were enrolled in exactly 2 courses and 4 students were enrolled in all three courses.
The students which were enrolled in all three sports, withdrew from one of the sports. Hence, we can say that now the number of students who were enrolled in exactly 2 courses = 11 + 4 = 15.
It is given that the number of students enrolled in G was six less than the number of students enrolled in L. Let 'a' be the number of students who were enrolled in G and K but not L. Then, the number of students who were enrolled in L and K but not G = a + 5
Consequently, we can say that the number of students enrolled in G and L but not K = 15 - (2a + 5) = 10 - 2a

Number of students enrolled in this case = a + a+5 + 9 = 14 + 2a. We can see that '14+2a' is an even number. It is given that the number of students enrolled in K went down by one. Therefore, we can say that the number of students
enrolled in K earlier was an odd number.
Hence, the number of students enrolled in K = 18 + z = {18, 19, 20}
We can see that only '19' is an odd number. Hence, we can say that the number of students enrolled in K after withdrawal = 18
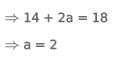

From the diagram we can see that the number of students enrolled in both G and K = 2.
Most Upvoted Answer
InstructionsFun Sports (FS) provides training in three sports - Gilli-...
Explanation:
Initial Enrollment:
- Let the number of students enrolled only in G be x.
- Number of students enrolled only in L = 2x (as per the given information).
- Number of students enrolled only in K = y.
- Number of students enrolled in both G and L = 10 (as per the given information).
- Number of students enrolled in both K and L = y (as per the given information).
- Total number of students enrolled in G = 17 (as per the given information).
- Total number of students enrolled in L = Maximum.
After Withdrawal:
- After withdrawal, number of students enrolled in G = 17 - 6 = 11.
- Number of students enrolled in L remains the same.
- Number of students enrolled in K = y - 1.
Final Enrollment:
- Let the number of students enrolled in both G and K be z.
- According to the information, the number of students enrolled only in G (11) is one less than the number of students enrolled only in L (2x).
- Therefore, 11 = 2x - 1.
- Solving the equation, we get x = 6.
- Number of students enrolled only in L = 2x = 12.
- Number of students enrolled only in K = y = 5.
- Number of students enrolled in both G and K = z.
Therefore, the number of students enrolled in both G and K after the withdrawal is 2.

|
Explore Courses for CAT exam
|

|
Similar CAT Doubts
InstructionsFun Sports (FS) provides training in three sports - Gilli-danda (G), Kho-Kho (K), and Ludo (L). Currently it has an enrollment of 39 students each of whom is enrolled in at least one of the three sports. The following details are known:1. The number of students enrolled only in L is double the number of students enrolled in all the three sports.2. There are a total of 17 students enrolled in G.3. The number of students enrolled only in G is one less than the number of students enrolled only in L.4. The number of students enrolled only in K is equal to the number of students who are enrolled in both K and L.5. The maximum student enrollment is in L.6. Ten students enrolled in G are also enrolled in at least one more sport.Q.Due to academic pressure, students who were enrolled in all three sports were asked to withdraw from one of the three sports. After the withdrawal, the number of students enrolled in G was six less than the number of students enrolled in L, while the number of students enrolled in K went down by one. After the withdrawal, how many students were enrolled in both G and K?Correct answer is '2'. Can you explain this answer?
Question Description
InstructionsFun Sports (FS) provides training in three sports - Gilli-danda (G), Kho-Kho (K), and Ludo (L). Currently it has an enrollment of 39 students each of whom is enrolled in at least one of the three sports. The following details are known:1. The number of students enrolled only in L is double the number of students enrolled in all the three sports.2. There are a total of 17 students enrolled in G.3. The number of students enrolled only in G is one less than the number of students enrolled only in L.4. The number of students enrolled only in K is equal to the number of students who are enrolled in both K and L.5. The maximum student enrollment is in L.6. Ten students enrolled in G are also enrolled in at least one more sport.Q.Due to academic pressure, students who were enrolled in all three sports were asked to withdraw from one of the three sports. After the withdrawal, the number of students enrolled in G was six less than the number of students enrolled in L, while the number of students enrolled in K went down by one. After the withdrawal, how many students were enrolled in both G and K?Correct answer is '2'. Can you explain this answer? for CAT 2025 is part of CAT preparation. The Question and answers have been prepared according to the CAT exam syllabus. Information about InstructionsFun Sports (FS) provides training in three sports - Gilli-danda (G), Kho-Kho (K), and Ludo (L). Currently it has an enrollment of 39 students each of whom is enrolled in at least one of the three sports. The following details are known:1. The number of students enrolled only in L is double the number of students enrolled in all the three sports.2. There are a total of 17 students enrolled in G.3. The number of students enrolled only in G is one less than the number of students enrolled only in L.4. The number of students enrolled only in K is equal to the number of students who are enrolled in both K and L.5. The maximum student enrollment is in L.6. Ten students enrolled in G are also enrolled in at least one more sport.Q.Due to academic pressure, students who were enrolled in all three sports were asked to withdraw from one of the three sports. After the withdrawal, the number of students enrolled in G was six less than the number of students enrolled in L, while the number of students enrolled in K went down by one. After the withdrawal, how many students were enrolled in both G and K?Correct answer is '2'. Can you explain this answer? covers all topics & solutions for CAT 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for InstructionsFun Sports (FS) provides training in three sports - Gilli-danda (G), Kho-Kho (K), and Ludo (L). Currently it has an enrollment of 39 students each of whom is enrolled in at least one of the three sports. The following details are known:1. The number of students enrolled only in L is double the number of students enrolled in all the three sports.2. There are a total of 17 students enrolled in G.3. The number of students enrolled only in G is one less than the number of students enrolled only in L.4. The number of students enrolled only in K is equal to the number of students who are enrolled in both K and L.5. The maximum student enrollment is in L.6. Ten students enrolled in G are also enrolled in at least one more sport.Q.Due to academic pressure, students who were enrolled in all three sports were asked to withdraw from one of the three sports. After the withdrawal, the number of students enrolled in G was six less than the number of students enrolled in L, while the number of students enrolled in K went down by one. After the withdrawal, how many students were enrolled in both G and K?Correct answer is '2'. Can you explain this answer?.
InstructionsFun Sports (FS) provides training in three sports - Gilli-danda (G), Kho-Kho (K), and Ludo (L). Currently it has an enrollment of 39 students each of whom is enrolled in at least one of the three sports. The following details are known:1. The number of students enrolled only in L is double the number of students enrolled in all the three sports.2. There are a total of 17 students enrolled in G.3. The number of students enrolled only in G is one less than the number of students enrolled only in L.4. The number of students enrolled only in K is equal to the number of students who are enrolled in both K and L.5. The maximum student enrollment is in L.6. Ten students enrolled in G are also enrolled in at least one more sport.Q.Due to academic pressure, students who were enrolled in all three sports were asked to withdraw from one of the three sports. After the withdrawal, the number of students enrolled in G was six less than the number of students enrolled in L, while the number of students enrolled in K went down by one. After the withdrawal, how many students were enrolled in both G and K?Correct answer is '2'. Can you explain this answer? for CAT 2025 is part of CAT preparation. The Question and answers have been prepared according to the CAT exam syllabus. Information about InstructionsFun Sports (FS) provides training in three sports - Gilli-danda (G), Kho-Kho (K), and Ludo (L). Currently it has an enrollment of 39 students each of whom is enrolled in at least one of the three sports. The following details are known:1. The number of students enrolled only in L is double the number of students enrolled in all the three sports.2. There are a total of 17 students enrolled in G.3. The number of students enrolled only in G is one less than the number of students enrolled only in L.4. The number of students enrolled only in K is equal to the number of students who are enrolled in both K and L.5. The maximum student enrollment is in L.6. Ten students enrolled in G are also enrolled in at least one more sport.Q.Due to academic pressure, students who were enrolled in all three sports were asked to withdraw from one of the three sports. After the withdrawal, the number of students enrolled in G was six less than the number of students enrolled in L, while the number of students enrolled in K went down by one. After the withdrawal, how many students were enrolled in both G and K?Correct answer is '2'. Can you explain this answer? covers all topics & solutions for CAT 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for InstructionsFun Sports (FS) provides training in three sports - Gilli-danda (G), Kho-Kho (K), and Ludo (L). Currently it has an enrollment of 39 students each of whom is enrolled in at least one of the three sports. The following details are known:1. The number of students enrolled only in L is double the number of students enrolled in all the three sports.2. There are a total of 17 students enrolled in G.3. The number of students enrolled only in G is one less than the number of students enrolled only in L.4. The number of students enrolled only in K is equal to the number of students who are enrolled in both K and L.5. The maximum student enrollment is in L.6. Ten students enrolled in G are also enrolled in at least one more sport.Q.Due to academic pressure, students who were enrolled in all three sports were asked to withdraw from one of the three sports. After the withdrawal, the number of students enrolled in G was six less than the number of students enrolled in L, while the number of students enrolled in K went down by one. After the withdrawal, how many students were enrolled in both G and K?Correct answer is '2'. Can you explain this answer?.
Solutions for InstructionsFun Sports (FS) provides training in three sports - Gilli-danda (G), Kho-Kho (K), and Ludo (L). Currently it has an enrollment of 39 students each of whom is enrolled in at least one of the three sports. The following details are known:1. The number of students enrolled only in L is double the number of students enrolled in all the three sports.2. There are a total of 17 students enrolled in G.3. The number of students enrolled only in G is one less than the number of students enrolled only in L.4. The number of students enrolled only in K is equal to the number of students who are enrolled in both K and L.5. The maximum student enrollment is in L.6. Ten students enrolled in G are also enrolled in at least one more sport.Q.Due to academic pressure, students who were enrolled in all three sports were asked to withdraw from one of the three sports. After the withdrawal, the number of students enrolled in G was six less than the number of students enrolled in L, while the number of students enrolled in K went down by one. After the withdrawal, how many students were enrolled in both G and K?Correct answer is '2'. Can you explain this answer? in English & in Hindi are available as part of our courses for CAT.
Download more important topics, notes, lectures and mock test series for CAT Exam by signing up for free.
Here you can find the meaning of InstructionsFun Sports (FS) provides training in three sports - Gilli-danda (G), Kho-Kho (K), and Ludo (L). Currently it has an enrollment of 39 students each of whom is enrolled in at least one of the three sports. The following details are known:1. The number of students enrolled only in L is double the number of students enrolled in all the three sports.2. There are a total of 17 students enrolled in G.3. The number of students enrolled only in G is one less than the number of students enrolled only in L.4. The number of students enrolled only in K is equal to the number of students who are enrolled in both K and L.5. The maximum student enrollment is in L.6. Ten students enrolled in G are also enrolled in at least one more sport.Q.Due to academic pressure, students who were enrolled in all three sports were asked to withdraw from one of the three sports. After the withdrawal, the number of students enrolled in G was six less than the number of students enrolled in L, while the number of students enrolled in K went down by one. After the withdrawal, how many students were enrolled in both G and K?Correct answer is '2'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
InstructionsFun Sports (FS) provides training in three sports - Gilli-danda (G), Kho-Kho (K), and Ludo (L). Currently it has an enrollment of 39 students each of whom is enrolled in at least one of the three sports. The following details are known:1. The number of students enrolled only in L is double the number of students enrolled in all the three sports.2. There are a total of 17 students enrolled in G.3. The number of students enrolled only in G is one less than the number of students enrolled only in L.4. The number of students enrolled only in K is equal to the number of students who are enrolled in both K and L.5. The maximum student enrollment is in L.6. Ten students enrolled in G are also enrolled in at least one more sport.Q.Due to academic pressure, students who were enrolled in all three sports were asked to withdraw from one of the three sports. After the withdrawal, the number of students enrolled in G was six less than the number of students enrolled in L, while the number of students enrolled in K went down by one. After the withdrawal, how many students were enrolled in both G and K?Correct answer is '2'. Can you explain this answer?, a detailed solution for InstructionsFun Sports (FS) provides training in three sports - Gilli-danda (G), Kho-Kho (K), and Ludo (L). Currently it has an enrollment of 39 students each of whom is enrolled in at least one of the three sports. The following details are known:1. The number of students enrolled only in L is double the number of students enrolled in all the three sports.2. There are a total of 17 students enrolled in G.3. The number of students enrolled only in G is one less than the number of students enrolled only in L.4. The number of students enrolled only in K is equal to the number of students who are enrolled in both K and L.5. The maximum student enrollment is in L.6. Ten students enrolled in G are also enrolled in at least one more sport.Q.Due to academic pressure, students who were enrolled in all three sports were asked to withdraw from one of the three sports. After the withdrawal, the number of students enrolled in G was six less than the number of students enrolled in L, while the number of students enrolled in K went down by one. After the withdrawal, how many students were enrolled in both G and K?Correct answer is '2'. Can you explain this answer? has been provided alongside types of InstructionsFun Sports (FS) provides training in three sports - Gilli-danda (G), Kho-Kho (K), and Ludo (L). Currently it has an enrollment of 39 students each of whom is enrolled in at least one of the three sports. The following details are known:1. The number of students enrolled only in L is double the number of students enrolled in all the three sports.2. There are a total of 17 students enrolled in G.3. The number of students enrolled only in G is one less than the number of students enrolled only in L.4. The number of students enrolled only in K is equal to the number of students who are enrolled in both K and L.5. The maximum student enrollment is in L.6. Ten students enrolled in G are also enrolled in at least one more sport.Q.Due to academic pressure, students who were enrolled in all three sports were asked to withdraw from one of the three sports. After the withdrawal, the number of students enrolled in G was six less than the number of students enrolled in L, while the number of students enrolled in K went down by one. After the withdrawal, how many students were enrolled in both G and K?Correct answer is '2'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice InstructionsFun Sports (FS) provides training in three sports - Gilli-danda (G), Kho-Kho (K), and Ludo (L). Currently it has an enrollment of 39 students each of whom is enrolled in at least one of the three sports. The following details are known:1. The number of students enrolled only in L is double the number of students enrolled in all the three sports.2. There are a total of 17 students enrolled in G.3. The number of students enrolled only in G is one less than the number of students enrolled only in L.4. The number of students enrolled only in K is equal to the number of students who are enrolled in both K and L.5. The maximum student enrollment is in L.6. Ten students enrolled in G are also enrolled in at least one more sport.Q.Due to academic pressure, students who were enrolled in all three sports were asked to withdraw from one of the three sports. After the withdrawal, the number of students enrolled in G was six less than the number of students enrolled in L, while the number of students enrolled in K went down by one. After the withdrawal, how many students were enrolled in both G and K?Correct answer is '2'. Can you explain this answer? tests, examples and also practice CAT tests.

|
Explore Courses for CAT exam
|

|
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.


























