Physics Exam > Physics Questions > A wire carrying current 4iand other carrying ...
Start Learning for Free
A wire carrying current 4i and other carrying current 2i in the same direction produce a magnetic field B at the mid-point. What will be the field when 2i current is switched off?
- a)2B
- b)4B
- c)B
- d)B/2
Correct answer is option 'C'. Can you explain this answer?
Verified Answer
A wire carrying current 4iand other carrying current2i in the same dir...
Magnetic field
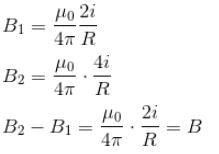
B2 = 2B1
2B1 – B1 = B
B1 = B
Most Upvoted Answer
A wire carrying current 4iand other carrying current2i in the same dir...
Magnetic field
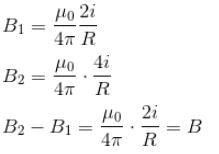
B2 = 2B1
2B1 – B1 = B
B1 = B
Free Test
FREE
| Start Free Test |
Community Answer
A wire carrying current 4iand other carrying current2i in the same dir...
Magnetic Field Produced by a Current-carrying Wire
When a wire carries a current, it produces a magnetic field around it. The magnitude of this magnetic field depends on the current and the distance from the wire. The direction of the magnetic field is given by the right-hand rule, where if you point your thumb in the direction of the current, your fingers curl in the direction of the magnetic field.
Magnetic Field Produced by Two Current-carrying Wires
When two wires carry currents in the same direction, the magnetic fields produced by each wire at a given point add up to create a stronger magnetic field. The magnitude of the magnetic field produced by each wire is given by the equation:
B = (μ0 * I) / (2π * r)
Where B is the magnetic field, μ0 is the permeability of free space (a constant), I is the current, and r is the distance from the wire.
Magnetic Field at the Mid-point
When two wires carrying currents i and 2i in the same direction are placed parallel to each other, the magnetic field at the mid-point is the sum of the magnetic fields produced by each wire. Let's call the magnetic field produced by the wire carrying current i as B1 and the magnetic field produced by the wire carrying current 2i as B2.
Initially, when both currents are present, the magnetic field at the mid-point is given by:
B = B1 + B2 = (μ0 * i) / (2π * r) + (μ0 * 2i) / (2π * r)
B = (μ0 * 3i) / (2π * r)
Switching Off the Current 2i
When the current 2i is switched off, we only have the current i flowing through one wire. Therefore, the magnetic field at the mid-point will only be due to the current i. The magnetic field can be calculated using the same equation:
B' = (μ0 * i) / (2π * r)
Comparing the Magnetic Fields
To determine the change in the magnetic field, we can compare the magnetic field when both currents are present (B) and when only the current i is present (B').
B / B' = [(μ0 * 3i) / (2π * r)] / [(μ0 * i) / (2π * r)]
B / B' = (3i) / i
B / B' = 3
Therefore, the magnetic field when the current 2i is switched off is three times smaller than the magnetic field when both currents are present. In other words, B' = B/3.
Hence, the correct answer is option c) B.
When a wire carries a current, it produces a magnetic field around it. The magnitude of this magnetic field depends on the current and the distance from the wire. The direction of the magnetic field is given by the right-hand rule, where if you point your thumb in the direction of the current, your fingers curl in the direction of the magnetic field.
Magnetic Field Produced by Two Current-carrying Wires
When two wires carry currents in the same direction, the magnetic fields produced by each wire at a given point add up to create a stronger magnetic field. The magnitude of the magnetic field produced by each wire is given by the equation:
B = (μ0 * I) / (2π * r)
Where B is the magnetic field, μ0 is the permeability of free space (a constant), I is the current, and r is the distance from the wire.
Magnetic Field at the Mid-point
When two wires carrying currents i and 2i in the same direction are placed parallel to each other, the magnetic field at the mid-point is the sum of the magnetic fields produced by each wire. Let's call the magnetic field produced by the wire carrying current i as B1 and the magnetic field produced by the wire carrying current 2i as B2.
Initially, when both currents are present, the magnetic field at the mid-point is given by:
B = B1 + B2 = (μ0 * i) / (2π * r) + (μ0 * 2i) / (2π * r)
B = (μ0 * 3i) / (2π * r)
Switching Off the Current 2i
When the current 2i is switched off, we only have the current i flowing through one wire. Therefore, the magnetic field at the mid-point will only be due to the current i. The magnetic field can be calculated using the same equation:
B' = (μ0 * i) / (2π * r)
Comparing the Magnetic Fields
To determine the change in the magnetic field, we can compare the magnetic field when both currents are present (B) and when only the current i is present (B').
B / B' = [(μ0 * 3i) / (2π * r)] / [(μ0 * i) / (2π * r)]
B / B' = (3i) / i
B / B' = 3
Therefore, the magnetic field when the current 2i is switched off is three times smaller than the magnetic field when both currents are present. In other words, B' = B/3.
Hence, the correct answer is option c) B.

|
Explore Courses for Physics exam
|

|
Question Description
A wire carrying current 4iand other carrying current2i in the same direction produce a magnetic fieldBat the mid-point. What will be the field when2icurrent is switched off?a)2Bb)4Bc)Bd)B/2Correct answer is option 'C'. Can you explain this answer? for Physics 2025 is part of Physics preparation. The Question and answers have been prepared according to the Physics exam syllabus. Information about A wire carrying current 4iand other carrying current2i in the same direction produce a magnetic fieldBat the mid-point. What will be the field when2icurrent is switched off?a)2Bb)4Bc)Bd)B/2Correct answer is option 'C'. Can you explain this answer? covers all topics & solutions for Physics 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for A wire carrying current 4iand other carrying current2i in the same direction produce a magnetic fieldBat the mid-point. What will be the field when2icurrent is switched off?a)2Bb)4Bc)Bd)B/2Correct answer is option 'C'. Can you explain this answer?.
A wire carrying current 4iand other carrying current2i in the same direction produce a magnetic fieldBat the mid-point. What will be the field when2icurrent is switched off?a)2Bb)4Bc)Bd)B/2Correct answer is option 'C'. Can you explain this answer? for Physics 2025 is part of Physics preparation. The Question and answers have been prepared according to the Physics exam syllabus. Information about A wire carrying current 4iand other carrying current2i in the same direction produce a magnetic fieldBat the mid-point. What will be the field when2icurrent is switched off?a)2Bb)4Bc)Bd)B/2Correct answer is option 'C'. Can you explain this answer? covers all topics & solutions for Physics 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for A wire carrying current 4iand other carrying current2i in the same direction produce a magnetic fieldBat the mid-point. What will be the field when2icurrent is switched off?a)2Bb)4Bc)Bd)B/2Correct answer is option 'C'. Can you explain this answer?.
Solutions for A wire carrying current 4iand other carrying current2i in the same direction produce a magnetic fieldBat the mid-point. What will be the field when2icurrent is switched off?a)2Bb)4Bc)Bd)B/2Correct answer is option 'C'. Can you explain this answer? in English & in Hindi are available as part of our courses for Physics.
Download more important topics, notes, lectures and mock test series for Physics Exam by signing up for free.
Here you can find the meaning of A wire carrying current 4iand other carrying current2i in the same direction produce a magnetic fieldBat the mid-point. What will be the field when2icurrent is switched off?a)2Bb)4Bc)Bd)B/2Correct answer is option 'C'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
A wire carrying current 4iand other carrying current2i in the same direction produce a magnetic fieldBat the mid-point. What will be the field when2icurrent is switched off?a)2Bb)4Bc)Bd)B/2Correct answer is option 'C'. Can you explain this answer?, a detailed solution for A wire carrying current 4iand other carrying current2i in the same direction produce a magnetic fieldBat the mid-point. What will be the field when2icurrent is switched off?a)2Bb)4Bc)Bd)B/2Correct answer is option 'C'. Can you explain this answer? has been provided alongside types of A wire carrying current 4iand other carrying current2i in the same direction produce a magnetic fieldBat the mid-point. What will be the field when2icurrent is switched off?a)2Bb)4Bc)Bd)B/2Correct answer is option 'C'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice A wire carrying current 4iand other carrying current2i in the same direction produce a magnetic fieldBat the mid-point. What will be the field when2icurrent is switched off?a)2Bb)4Bc)Bd)B/2Correct answer is option 'C'. Can you explain this answer? tests, examples and also practice Physics tests.

|
Explore Courses for Physics exam
|

|
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.























