Defence Exam > Defence Questions > From a height of h units, a man observes the ...
Start Learning for Free
From a height of h units, a man observes the angle of elevation as α and angle of depression as β of the top and bottom respectively of a tower of height H (> 4h). To what further height should be climb so that the values of angle of elevation and angle of depression get interchanged for the top and bottom of the tower?
- a)H - h units
- b)H - 2h units
- c)H - 3h units
- d)H - 4h units
Correct answer is option 'B'. Can you explain this answer?
| FREE This question is part of | Download PDF Attempt this Test |
Verified Answer
From a height of h units, a man observes the angle of elevation as &al...
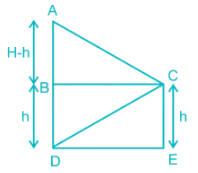
∠ACB = α and ∠BCD = β initially
In triangle BCD, cot β = BC/BD
∴ BC = BD cot β = h cot β
In triangle ABC, tan α = AB/BC
∴ AB = BC tan α
H - h = h cotβ × tan α ----1
∴ H = h (cotβ tan α + 1) ----2
In triangle BCD, cot β = BC/BD
∴ BC = BD cot β = h cot β
In triangle ABC, tan α = AB/BC
∴ AB = BC tan α
H - h = h cotβ × tan α ----1
∴ H = h (cotβ tan α + 1) ----2
Now height changes to h’ and the angles get interchanged
∴ H = h’ (cot α tanβ + 1) ----3
∴ H = h’ (cot α tanβ + 1) ----3
Equating the RHS of equations 2 and 3
h(cotβ tan α + 1) = h’(cot α tan β + 1)
h (1/tanβ × tanα + 1) = h’ (1/tan α × tan β + 1) [∵ tan A = 1/cot A]
h (tan α + tan β)/tan β = h’ (tan α + tan β)/tan α
∴ h’ = h/tan β × tan α
∴ h’ = h/tan β × tan α
⇒ h cot β × tan α = H - h [From equation 1]
∴ h’ = H - h
∴ h’ = H - h
Increase in height = h’ - h = H - h - h = H - 2h units
Shortcut:
Since the distance between the building does not change [BC]
If the angle interchanges corresponding height portion of the tallest building should be interchanged
Length of AB in original case = Length of BD in new case
H - h = h’
∴ h’ - h = H - 2h units
∴ h’ - h = H - 2h units
Most Upvoted Answer
From a height of h units, a man observes the angle of elevation as &al...
X. If the man moves a distance of d units closer to the object, his angle of elevation increases to y. We can use these observations to find the height of the object.
First, let's draw a diagram to visualize the situation:
```
A
|\
h | \ x
| \
| \
| \
| \
| \
| \
| \
|__________\
d B
```
In this diagram, A represents the man's original position, B represents the object, and AB represents the distance between the man and the object.
We are given that the angle of elevation from A to B is x. This means that angle A is a right angle (90 degrees) and angle B is equal to x.
When the man moves closer to the object, his new position is represented by C:
```
A
|\
h | \ x
| \
| \
| \
| \
| \
| \
| \
d | \
|__________\
C B
```
In this diagram, C represents the man's new position, and BC represents the distance between the man and the object.
We are given that the angle of elevation from C to B is y. This means that angle C is now a right angle (90 degrees) and angle B is equal to y.
From this diagram, we can create two right triangles: triangle ABC and triangle BCD.
In triangle ABC, we have angle A = 90 degrees, angle B = x, and side AC = h.
In triangle BCD, we have angle C = 90 degrees, angle B = y, and side BC = d.
Using basic trigonometry, we can write the following equations based on these triangles:
1) tan(x) = h / AC
2) tan(y) = h / BC
Since AC = BC - d, we can substitute this into equation 1:
1') tan(x) = h / (BC - d)
Now, we can solve these two equations for h.
From equation 2, we can solve for h:
h = tan(y) * BC
Substituting this into equation 1':
tan(x) = (tan(y) * BC) / (BC - d)
To solve for BC, we can rearrange the equation as follows:
tan(x) * (BC - d) = tan(y) * BC
tan(x) * BC - tan(x) * d = tan(y) * BC
tan(x) * BC - tan(y) * BC = tan(x) * d
BC * (tan(x) - tan(y)) = tan(x) * d
BC = (tan(x) * d) / (tan(x) - tan(y))
Now that we have BC, we can substitute it back into equation 2 to solve for h:
h = tan(y) * BC
h = tan(y) * ((tan(x) * d) / (tan(x) - tan(y)))
Therefore, the height of the object is given by:
h = (tan(x) * tan(y) * d) / (tan(x) - tan(y))
Note: It's important to ensure that the angles x and y are measured
First, let's draw a diagram to visualize the situation:
```
A
|\
h | \ x
| \
| \
| \
| \
| \
| \
| \
|__________\
d B
```
In this diagram, A represents the man's original position, B represents the object, and AB represents the distance between the man and the object.
We are given that the angle of elevation from A to B is x. This means that angle A is a right angle (90 degrees) and angle B is equal to x.
When the man moves closer to the object, his new position is represented by C:
```
A
|\
h | \ x
| \
| \
| \
| \
| \
| \
| \
d | \
|__________\
C B
```
In this diagram, C represents the man's new position, and BC represents the distance between the man and the object.
We are given that the angle of elevation from C to B is y. This means that angle C is now a right angle (90 degrees) and angle B is equal to y.
From this diagram, we can create two right triangles: triangle ABC and triangle BCD.
In triangle ABC, we have angle A = 90 degrees, angle B = x, and side AC = h.
In triangle BCD, we have angle C = 90 degrees, angle B = y, and side BC = d.
Using basic trigonometry, we can write the following equations based on these triangles:
1) tan(x) = h / AC
2) tan(y) = h / BC
Since AC = BC - d, we can substitute this into equation 1:
1') tan(x) = h / (BC - d)
Now, we can solve these two equations for h.
From equation 2, we can solve for h:
h = tan(y) * BC
Substituting this into equation 1':
tan(x) = (tan(y) * BC) / (BC - d)
To solve for BC, we can rearrange the equation as follows:
tan(x) * (BC - d) = tan(y) * BC
tan(x) * BC - tan(x) * d = tan(y) * BC
tan(x) * BC - tan(y) * BC = tan(x) * d
BC * (tan(x) - tan(y)) = tan(x) * d
BC = (tan(x) * d) / (tan(x) - tan(y))
Now that we have BC, we can substitute it back into equation 2 to solve for h:
h = tan(y) * BC
h = tan(y) * ((tan(x) * d) / (tan(x) - tan(y)))
Therefore, the height of the object is given by:
h = (tan(x) * tan(y) * d) / (tan(x) - tan(y))
Note: It's important to ensure that the angles x and y are measured

|
Explore Courses for Defence exam
|

|
Similar Defence Doubts
From a height of h units, a man observes the angle of elevation as α and angle of depression as β of the top and bottom respectively of a tower of height H (> 4h). To what further height should be climb so that the values of angle of elevation and angle of depression get interchanged for the top and bottom of the tower?a)H - h unitsb)H - 2h unitsc)H - 3h unitsd)H - 4h unitsCorrect answer is option 'B'. Can you explain this answer?
Question Description
From a height of h units, a man observes the angle of elevation as α and angle of depression as β of the top and bottom respectively of a tower of height H (> 4h). To what further height should be climb so that the values of angle of elevation and angle of depression get interchanged for the top and bottom of the tower?a)H - h unitsb)H - 2h unitsc)H - 3h unitsd)H - 4h unitsCorrect answer is option 'B'. Can you explain this answer? for Defence 2024 is part of Defence preparation. The Question and answers have been prepared according to the Defence exam syllabus. Information about From a height of h units, a man observes the angle of elevation as α and angle of depression as β of the top and bottom respectively of a tower of height H (> 4h). To what further height should be climb so that the values of angle of elevation and angle of depression get interchanged for the top and bottom of the tower?a)H - h unitsb)H - 2h unitsc)H - 3h unitsd)H - 4h unitsCorrect answer is option 'B'. Can you explain this answer? covers all topics & solutions for Defence 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for From a height of h units, a man observes the angle of elevation as α and angle of depression as β of the top and bottom respectively of a tower of height H (> 4h). To what further height should be climb so that the values of angle of elevation and angle of depression get interchanged for the top and bottom of the tower?a)H - h unitsb)H - 2h unitsc)H - 3h unitsd)H - 4h unitsCorrect answer is option 'B'. Can you explain this answer?.
From a height of h units, a man observes the angle of elevation as α and angle of depression as β of the top and bottom respectively of a tower of height H (> 4h). To what further height should be climb so that the values of angle of elevation and angle of depression get interchanged for the top and bottom of the tower?a)H - h unitsb)H - 2h unitsc)H - 3h unitsd)H - 4h unitsCorrect answer is option 'B'. Can you explain this answer? for Defence 2024 is part of Defence preparation. The Question and answers have been prepared according to the Defence exam syllabus. Information about From a height of h units, a man observes the angle of elevation as α and angle of depression as β of the top and bottom respectively of a tower of height H (> 4h). To what further height should be climb so that the values of angle of elevation and angle of depression get interchanged for the top and bottom of the tower?a)H - h unitsb)H - 2h unitsc)H - 3h unitsd)H - 4h unitsCorrect answer is option 'B'. Can you explain this answer? covers all topics & solutions for Defence 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for From a height of h units, a man observes the angle of elevation as α and angle of depression as β of the top and bottom respectively of a tower of height H (> 4h). To what further height should be climb so that the values of angle of elevation and angle of depression get interchanged for the top and bottom of the tower?a)H - h unitsb)H - 2h unitsc)H - 3h unitsd)H - 4h unitsCorrect answer is option 'B'. Can you explain this answer?.
Solutions for From a height of h units, a man observes the angle of elevation as α and angle of depression as β of the top and bottom respectively of a tower of height H (> 4h). To what further height should be climb so that the values of angle of elevation and angle of depression get interchanged for the top and bottom of the tower?a)H - h unitsb)H - 2h unitsc)H - 3h unitsd)H - 4h unitsCorrect answer is option 'B'. Can you explain this answer? in English & in Hindi are available as part of our courses for Defence.
Download more important topics, notes, lectures and mock test series for Defence Exam by signing up for free.
Here you can find the meaning of From a height of h units, a man observes the angle of elevation as α and angle of depression as β of the top and bottom respectively of a tower of height H (> 4h). To what further height should be climb so that the values of angle of elevation and angle of depression get interchanged for the top and bottom of the tower?a)H - h unitsb)H - 2h unitsc)H - 3h unitsd)H - 4h unitsCorrect answer is option 'B'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
From a height of h units, a man observes the angle of elevation as α and angle of depression as β of the top and bottom respectively of a tower of height H (> 4h). To what further height should be climb so that the values of angle of elevation and angle of depression get interchanged for the top and bottom of the tower?a)H - h unitsb)H - 2h unitsc)H - 3h unitsd)H - 4h unitsCorrect answer is option 'B'. Can you explain this answer?, a detailed solution for From a height of h units, a man observes the angle of elevation as α and angle of depression as β of the top and bottom respectively of a tower of height H (> 4h). To what further height should be climb so that the values of angle of elevation and angle of depression get interchanged for the top and bottom of the tower?a)H - h unitsb)H - 2h unitsc)H - 3h unitsd)H - 4h unitsCorrect answer is option 'B'. Can you explain this answer? has been provided alongside types of From a height of h units, a man observes the angle of elevation as α and angle of depression as β of the top and bottom respectively of a tower of height H (> 4h). To what further height should be climb so that the values of angle of elevation and angle of depression get interchanged for the top and bottom of the tower?a)H - h unitsb)H - 2h unitsc)H - 3h unitsd)H - 4h unitsCorrect answer is option 'B'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice From a height of h units, a man observes the angle of elevation as α and angle of depression as β of the top and bottom respectively of a tower of height H (> 4h). To what further height should be climb so that the values of angle of elevation and angle of depression get interchanged for the top and bottom of the tower?a)H - h unitsb)H - 2h unitsc)H - 3h unitsd)H - 4h unitsCorrect answer is option 'B'. Can you explain this answer? tests, examples and also practice Defence tests.

|
Explore Courses for Defence exam
|

|
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.


















