JEE Exam > JEE Questions > Consider two liquids B and C that form an ide...
Start Learning for Free
Consider two liquids ‘B’ and ‘C’ that form an ideal solutlion. We hold the temperature fixed at some value T that is above the freezing points of ‘B’ and ‘C’ .We shall plot the system’s pressure P and against XB’ the overall mole fraction of B in the system :
Where nbl and nbv are the number of moles of B in the liquid and vapor phases, respectively. For a close system xB, is fixed, although nBl and nBv may vary.
Let the system be enclosed in a cylinder fitted with a piston and immersed in a constant-temperature bath.To see what the P-versus-xB phase diagram looks like, let us initially set the external pressure on the piston high enough for the system to be entirely liquid (point A in figure) As the pressure is lowered below that at A, the system eventually reaches a pressure where the liquid just begins to vaporizes (point D). At point D, the liquid has composition xlb where xlb at D is equal to the overall mole fraction xB since only an infinitesimal amount of liquid has vapourized. What is the composition of the first vapour that comes off ? Raoult's law, Pb=xvbPob relates the vapour-phase mole fractions to the liquid composition as follows:
Where Pob and Pocare the vapour pressures of pure 'B' and pure 'C' at T, where the system's pressure P equals the sum PB + Pc of the partial pressures, where 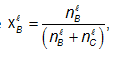 and the vapor is assumed ideal.
and the vapor is assumed ideal.
Let B be the more volatile component, meaning that Pob>Poc Above equation then shows that Xvb/Xvc>Xlb/XlcThe vapor above an ideal solution is richer than the liquid in the more volatile component. Equations (1) and (2) apply at any pressure where liquid -vapor equilibrium exists, not just at point D.
Now let us isothermally lower the pressure below point D, causing more liquid to vaporize. Eventually, WE reach point F in figure, where the last drop of liquid vaporizes. Below F, we have only vapor. For any point or the line between D and F liquid and vapor phases coexist in equilibrium.
Q.
The equation of the curve obtained by connecting all those points where the vapors of above mixture (all mixtures of different composition are taken) just start forming will be
- a)
- b)
- c)
- d)
Correct answer is option 'A'. Can you explain this answer?
| FREE This question is part of | Download PDF Attempt this Test |
Verified Answer
Consider two liquids B and C that form an ideal solutlion. We hold the...
Form solution of above question

|
Explore Courses for JEE exam
|

|
Similar JEE Doubts
Consider two liquids B and C that form an ideal solutlion. We hold the temperature fixed at some value T that is above the freezing points of B and C .We shall plot the systems pressure P and against XB the overall mole fraction of B in the system :Where nbland nbvare the number of moles of B in the liquid and vapor phases, respectively. For a close system xB, is fixed, although nBland nBvmay vary. Let the system be enclosed in a cylinder fitted with a piston and immersed in a constant-temperature bath.To see what the P-versus-xB phase diagram looks like, let us initially set the external pressure on the piston high enough for the system to be entirely liquid (point A in figure) As the pressure is lowered below that at A, the system eventually reaches a pressure where the liquid just begins to vaporizes (point D). At point D, the liquid has composition xlbwhere xlbat D is equal to the overall mole fraction xB since only an infinitesimal amount of liquid has vapourized. What is the composition of the first vapour that comes off ? Raoults law, Pb=xvbPobrelates the vapour-phase mole fractions to the liquid composition as follows:Where Poband Pocare the vapour pressures of pure B and pure C at T, where the systems pressure P equals the sum PB + Pc of the partial pressures, where and the vapor is assumed ideal.Let B be the more volatile component, meaning that PobPocAbove equation then shows that Xvb/XvcXlb/XlcThe vapor above an ideal solution is richer than the liquid in the more volatile component. Equations (1) and (2) apply at any pressure where liquid -vapor equilibrium exists, not just at point D. Now let us isothermally lower the pressure below point D, causing more liquid to vaporize. Eventually, WE reach point F in figure, where the last drop of liquid vaporizes. Below F, we have only vapor. For any point or the line between D and F liquid and vapor phases coexist in equilibrium.Q.The equation of the curve obtained by connecting all those points where the vapors of above mixture (all mixtures of different composition are taken) just start forming will bea)b)c)d)Correct answer is option 'A'. Can you explain this answer?
Question Description
Consider two liquids B and C that form an ideal solutlion. We hold the temperature fixed at some value T that is above the freezing points of B and C .We shall plot the systems pressure P and against XB the overall mole fraction of B in the system :Where nbland nbvare the number of moles of B in the liquid and vapor phases, respectively. For a close system xB, is fixed, although nBland nBvmay vary. Let the system be enclosed in a cylinder fitted with a piston and immersed in a constant-temperature bath.To see what the P-versus-xB phase diagram looks like, let us initially set the external pressure on the piston high enough for the system to be entirely liquid (point A in figure) As the pressure is lowered below that at A, the system eventually reaches a pressure where the liquid just begins to vaporizes (point D). At point D, the liquid has composition xlbwhere xlbat D is equal to the overall mole fraction xB since only an infinitesimal amount of liquid has vapourized. What is the composition of the first vapour that comes off ? Raoults law, Pb=xvbPobrelates the vapour-phase mole fractions to the liquid composition as follows:Where Poband Pocare the vapour pressures of pure B and pure C at T, where the systems pressure P equals the sum PB + Pc of the partial pressures, where and the vapor is assumed ideal.Let B be the more volatile component, meaning that PobPocAbove equation then shows that Xvb/XvcXlb/XlcThe vapor above an ideal solution is richer than the liquid in the more volatile component. Equations (1) and (2) apply at any pressure where liquid -vapor equilibrium exists, not just at point D. Now let us isothermally lower the pressure below point D, causing more liquid to vaporize. Eventually, WE reach point F in figure, where the last drop of liquid vaporizes. Below F, we have only vapor. For any point or the line between D and F liquid and vapor phases coexist in equilibrium.Q.The equation of the curve obtained by connecting all those points where the vapors of above mixture (all mixtures of different composition are taken) just start forming will bea)b)c)d)Correct answer is option 'A'. Can you explain this answer? for JEE 2024 is part of JEE preparation. The Question and answers have been prepared according to the JEE exam syllabus. Information about Consider two liquids B and C that form an ideal solutlion. We hold the temperature fixed at some value T that is above the freezing points of B and C .We shall plot the systems pressure P and against XB the overall mole fraction of B in the system :Where nbland nbvare the number of moles of B in the liquid and vapor phases, respectively. For a close system xB, is fixed, although nBland nBvmay vary. Let the system be enclosed in a cylinder fitted with a piston and immersed in a constant-temperature bath.To see what the P-versus-xB phase diagram looks like, let us initially set the external pressure on the piston high enough for the system to be entirely liquid (point A in figure) As the pressure is lowered below that at A, the system eventually reaches a pressure where the liquid just begins to vaporizes (point D). At point D, the liquid has composition xlbwhere xlbat D is equal to the overall mole fraction xB since only an infinitesimal amount of liquid has vapourized. What is the composition of the first vapour that comes off ? Raoults law, Pb=xvbPobrelates the vapour-phase mole fractions to the liquid composition as follows:Where Poband Pocare the vapour pressures of pure B and pure C at T, where the systems pressure P equals the sum PB + Pc of the partial pressures, where and the vapor is assumed ideal.Let B be the more volatile component, meaning that PobPocAbove equation then shows that Xvb/XvcXlb/XlcThe vapor above an ideal solution is richer than the liquid in the more volatile component. Equations (1) and (2) apply at any pressure where liquid -vapor equilibrium exists, not just at point D. Now let us isothermally lower the pressure below point D, causing more liquid to vaporize. Eventually, WE reach point F in figure, where the last drop of liquid vaporizes. Below F, we have only vapor. For any point or the line between D and F liquid and vapor phases coexist in equilibrium.Q.The equation of the curve obtained by connecting all those points where the vapors of above mixture (all mixtures of different composition are taken) just start forming will bea)b)c)d)Correct answer is option 'A'. Can you explain this answer? covers all topics & solutions for JEE 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for Consider two liquids B and C that form an ideal solutlion. We hold the temperature fixed at some value T that is above the freezing points of B and C .We shall plot the systems pressure P and against XB the overall mole fraction of B in the system :Where nbland nbvare the number of moles of B in the liquid and vapor phases, respectively. For a close system xB, is fixed, although nBland nBvmay vary. Let the system be enclosed in a cylinder fitted with a piston and immersed in a constant-temperature bath.To see what the P-versus-xB phase diagram looks like, let us initially set the external pressure on the piston high enough for the system to be entirely liquid (point A in figure) As the pressure is lowered below that at A, the system eventually reaches a pressure where the liquid just begins to vaporizes (point D). At point D, the liquid has composition xlbwhere xlbat D is equal to the overall mole fraction xB since only an infinitesimal amount of liquid has vapourized. What is the composition of the first vapour that comes off ? Raoults law, Pb=xvbPobrelates the vapour-phase mole fractions to the liquid composition as follows:Where Poband Pocare the vapour pressures of pure B and pure C at T, where the systems pressure P equals the sum PB + Pc of the partial pressures, where and the vapor is assumed ideal.Let B be the more volatile component, meaning that PobPocAbove equation then shows that Xvb/XvcXlb/XlcThe vapor above an ideal solution is richer than the liquid in the more volatile component. Equations (1) and (2) apply at any pressure where liquid -vapor equilibrium exists, not just at point D. Now let us isothermally lower the pressure below point D, causing more liquid to vaporize. Eventually, WE reach point F in figure, where the last drop of liquid vaporizes. Below F, we have only vapor. For any point or the line between D and F liquid and vapor phases coexist in equilibrium.Q.The equation of the curve obtained by connecting all those points where the vapors of above mixture (all mixtures of different composition are taken) just start forming will bea)b)c)d)Correct answer is option 'A'. Can you explain this answer?.
Consider two liquids B and C that form an ideal solutlion. We hold the temperature fixed at some value T that is above the freezing points of B and C .We shall plot the systems pressure P and against XB the overall mole fraction of B in the system :Where nbland nbvare the number of moles of B in the liquid and vapor phases, respectively. For a close system xB, is fixed, although nBland nBvmay vary. Let the system be enclosed in a cylinder fitted with a piston and immersed in a constant-temperature bath.To see what the P-versus-xB phase diagram looks like, let us initially set the external pressure on the piston high enough for the system to be entirely liquid (point A in figure) As the pressure is lowered below that at A, the system eventually reaches a pressure where the liquid just begins to vaporizes (point D). At point D, the liquid has composition xlbwhere xlbat D is equal to the overall mole fraction xB since only an infinitesimal amount of liquid has vapourized. What is the composition of the first vapour that comes off ? Raoults law, Pb=xvbPobrelates the vapour-phase mole fractions to the liquid composition as follows:Where Poband Pocare the vapour pressures of pure B and pure C at T, where the systems pressure P equals the sum PB + Pc of the partial pressures, where and the vapor is assumed ideal.Let B be the more volatile component, meaning that PobPocAbove equation then shows that Xvb/XvcXlb/XlcThe vapor above an ideal solution is richer than the liquid in the more volatile component. Equations (1) and (2) apply at any pressure where liquid -vapor equilibrium exists, not just at point D. Now let us isothermally lower the pressure below point D, causing more liquid to vaporize. Eventually, WE reach point F in figure, where the last drop of liquid vaporizes. Below F, we have only vapor. For any point or the line between D and F liquid and vapor phases coexist in equilibrium.Q.The equation of the curve obtained by connecting all those points where the vapors of above mixture (all mixtures of different composition are taken) just start forming will bea)b)c)d)Correct answer is option 'A'. Can you explain this answer? for JEE 2024 is part of JEE preparation. The Question and answers have been prepared according to the JEE exam syllabus. Information about Consider two liquids B and C that form an ideal solutlion. We hold the temperature fixed at some value T that is above the freezing points of B and C .We shall plot the systems pressure P and against XB the overall mole fraction of B in the system :Where nbland nbvare the number of moles of B in the liquid and vapor phases, respectively. For a close system xB, is fixed, although nBland nBvmay vary. Let the system be enclosed in a cylinder fitted with a piston and immersed in a constant-temperature bath.To see what the P-versus-xB phase diagram looks like, let us initially set the external pressure on the piston high enough for the system to be entirely liquid (point A in figure) As the pressure is lowered below that at A, the system eventually reaches a pressure where the liquid just begins to vaporizes (point D). At point D, the liquid has composition xlbwhere xlbat D is equal to the overall mole fraction xB since only an infinitesimal amount of liquid has vapourized. What is the composition of the first vapour that comes off ? Raoults law, Pb=xvbPobrelates the vapour-phase mole fractions to the liquid composition as follows:Where Poband Pocare the vapour pressures of pure B and pure C at T, where the systems pressure P equals the sum PB + Pc of the partial pressures, where and the vapor is assumed ideal.Let B be the more volatile component, meaning that PobPocAbove equation then shows that Xvb/XvcXlb/XlcThe vapor above an ideal solution is richer than the liquid in the more volatile component. Equations (1) and (2) apply at any pressure where liquid -vapor equilibrium exists, not just at point D. Now let us isothermally lower the pressure below point D, causing more liquid to vaporize. Eventually, WE reach point F in figure, where the last drop of liquid vaporizes. Below F, we have only vapor. For any point or the line between D and F liquid and vapor phases coexist in equilibrium.Q.The equation of the curve obtained by connecting all those points where the vapors of above mixture (all mixtures of different composition are taken) just start forming will bea)b)c)d)Correct answer is option 'A'. Can you explain this answer? covers all topics & solutions for JEE 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for Consider two liquids B and C that form an ideal solutlion. We hold the temperature fixed at some value T that is above the freezing points of B and C .We shall plot the systems pressure P and against XB the overall mole fraction of B in the system :Where nbland nbvare the number of moles of B in the liquid and vapor phases, respectively. For a close system xB, is fixed, although nBland nBvmay vary. Let the system be enclosed in a cylinder fitted with a piston and immersed in a constant-temperature bath.To see what the P-versus-xB phase diagram looks like, let us initially set the external pressure on the piston high enough for the system to be entirely liquid (point A in figure) As the pressure is lowered below that at A, the system eventually reaches a pressure where the liquid just begins to vaporizes (point D). At point D, the liquid has composition xlbwhere xlbat D is equal to the overall mole fraction xB since only an infinitesimal amount of liquid has vapourized. What is the composition of the first vapour that comes off ? Raoults law, Pb=xvbPobrelates the vapour-phase mole fractions to the liquid composition as follows:Where Poband Pocare the vapour pressures of pure B and pure C at T, where the systems pressure P equals the sum PB + Pc of the partial pressures, where and the vapor is assumed ideal.Let B be the more volatile component, meaning that PobPocAbove equation then shows that Xvb/XvcXlb/XlcThe vapor above an ideal solution is richer than the liquid in the more volatile component. Equations (1) and (2) apply at any pressure where liquid -vapor equilibrium exists, not just at point D. Now let us isothermally lower the pressure below point D, causing more liquid to vaporize. Eventually, WE reach point F in figure, where the last drop of liquid vaporizes. Below F, we have only vapor. For any point or the line between D and F liquid and vapor phases coexist in equilibrium.Q.The equation of the curve obtained by connecting all those points where the vapors of above mixture (all mixtures of different composition are taken) just start forming will bea)b)c)d)Correct answer is option 'A'. Can you explain this answer?.
Solutions for Consider two liquids B and C that form an ideal solutlion. We hold the temperature fixed at some value T that is above the freezing points of B and C .We shall plot the systems pressure P and against XB the overall mole fraction of B in the system :Where nbland nbvare the number of moles of B in the liquid and vapor phases, respectively. For a close system xB, is fixed, although nBland nBvmay vary. Let the system be enclosed in a cylinder fitted with a piston and immersed in a constant-temperature bath.To see what the P-versus-xB phase diagram looks like, let us initially set the external pressure on the piston high enough for the system to be entirely liquid (point A in figure) As the pressure is lowered below that at A, the system eventually reaches a pressure where the liquid just begins to vaporizes (point D). At point D, the liquid has composition xlbwhere xlbat D is equal to the overall mole fraction xB since only an infinitesimal amount of liquid has vapourized. What is the composition of the first vapour that comes off ? Raoults law, Pb=xvbPobrelates the vapour-phase mole fractions to the liquid composition as follows:Where Poband Pocare the vapour pressures of pure B and pure C at T, where the systems pressure P equals the sum PB + Pc of the partial pressures, where and the vapor is assumed ideal.Let B be the more volatile component, meaning that PobPocAbove equation then shows that Xvb/XvcXlb/XlcThe vapor above an ideal solution is richer than the liquid in the more volatile component. Equations (1) and (2) apply at any pressure where liquid -vapor equilibrium exists, not just at point D. Now let us isothermally lower the pressure below point D, causing more liquid to vaporize. Eventually, WE reach point F in figure, where the last drop of liquid vaporizes. Below F, we have only vapor. For any point or the line between D and F liquid and vapor phases coexist in equilibrium.Q.The equation of the curve obtained by connecting all those points where the vapors of above mixture (all mixtures of different composition are taken) just start forming will bea)b)c)d)Correct answer is option 'A'. Can you explain this answer? in English & in Hindi are available as part of our courses for JEE.
Download more important topics, notes, lectures and mock test series for JEE Exam by signing up for free.
Here you can find the meaning of Consider two liquids B and C that form an ideal solutlion. We hold the temperature fixed at some value T that is above the freezing points of B and C .We shall plot the systems pressure P and against XB the overall mole fraction of B in the system :Where nbland nbvare the number of moles of B in the liquid and vapor phases, respectively. For a close system xB, is fixed, although nBland nBvmay vary. Let the system be enclosed in a cylinder fitted with a piston and immersed in a constant-temperature bath.To see what the P-versus-xB phase diagram looks like, let us initially set the external pressure on the piston high enough for the system to be entirely liquid (point A in figure) As the pressure is lowered below that at A, the system eventually reaches a pressure where the liquid just begins to vaporizes (point D). At point D, the liquid has composition xlbwhere xlbat D is equal to the overall mole fraction xB since only an infinitesimal amount of liquid has vapourized. What is the composition of the first vapour that comes off ? Raoults law, Pb=xvbPobrelates the vapour-phase mole fractions to the liquid composition as follows:Where Poband Pocare the vapour pressures of pure B and pure C at T, where the systems pressure P equals the sum PB + Pc of the partial pressures, where and the vapor is assumed ideal.Let B be the more volatile component, meaning that PobPocAbove equation then shows that Xvb/XvcXlb/XlcThe vapor above an ideal solution is richer than the liquid in the more volatile component. Equations (1) and (2) apply at any pressure where liquid -vapor equilibrium exists, not just at point D. Now let us isothermally lower the pressure below point D, causing more liquid to vaporize. Eventually, WE reach point F in figure, where the last drop of liquid vaporizes. Below F, we have only vapor. For any point or the line between D and F liquid and vapor phases coexist in equilibrium.Q.The equation of the curve obtained by connecting all those points where the vapors of above mixture (all mixtures of different composition are taken) just start forming will bea)b)c)d)Correct answer is option 'A'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
Consider two liquids B and C that form an ideal solutlion. We hold the temperature fixed at some value T that is above the freezing points of B and C .We shall plot the systems pressure P and against XB the overall mole fraction of B in the system :Where nbland nbvare the number of moles of B in the liquid and vapor phases, respectively. For a close system xB, is fixed, although nBland nBvmay vary. Let the system be enclosed in a cylinder fitted with a piston and immersed in a constant-temperature bath.To see what the P-versus-xB phase diagram looks like, let us initially set the external pressure on the piston high enough for the system to be entirely liquid (point A in figure) As the pressure is lowered below that at A, the system eventually reaches a pressure where the liquid just begins to vaporizes (point D). At point D, the liquid has composition xlbwhere xlbat D is equal to the overall mole fraction xB since only an infinitesimal amount of liquid has vapourized. What is the composition of the first vapour that comes off ? Raoults law, Pb=xvbPobrelates the vapour-phase mole fractions to the liquid composition as follows:Where Poband Pocare the vapour pressures of pure B and pure C at T, where the systems pressure P equals the sum PB + Pc of the partial pressures, where and the vapor is assumed ideal.Let B be the more volatile component, meaning that PobPocAbove equation then shows that Xvb/XvcXlb/XlcThe vapor above an ideal solution is richer than the liquid in the more volatile component. Equations (1) and (2) apply at any pressure where liquid -vapor equilibrium exists, not just at point D. Now let us isothermally lower the pressure below point D, causing more liquid to vaporize. Eventually, WE reach point F in figure, where the last drop of liquid vaporizes. Below F, we have only vapor. For any point or the line between D and F liquid and vapor phases coexist in equilibrium.Q.The equation of the curve obtained by connecting all those points where the vapors of above mixture (all mixtures of different composition are taken) just start forming will bea)b)c)d)Correct answer is option 'A'. Can you explain this answer?, a detailed solution for Consider two liquids B and C that form an ideal solutlion. We hold the temperature fixed at some value T that is above the freezing points of B and C .We shall plot the systems pressure P and against XB the overall mole fraction of B in the system :Where nbland nbvare the number of moles of B in the liquid and vapor phases, respectively. For a close system xB, is fixed, although nBland nBvmay vary. Let the system be enclosed in a cylinder fitted with a piston and immersed in a constant-temperature bath.To see what the P-versus-xB phase diagram looks like, let us initially set the external pressure on the piston high enough for the system to be entirely liquid (point A in figure) As the pressure is lowered below that at A, the system eventually reaches a pressure where the liquid just begins to vaporizes (point D). At point D, the liquid has composition xlbwhere xlbat D is equal to the overall mole fraction xB since only an infinitesimal amount of liquid has vapourized. What is the composition of the first vapour that comes off ? Raoults law, Pb=xvbPobrelates the vapour-phase mole fractions to the liquid composition as follows:Where Poband Pocare the vapour pressures of pure B and pure C at T, where the systems pressure P equals the sum PB + Pc of the partial pressures, where and the vapor is assumed ideal.Let B be the more volatile component, meaning that PobPocAbove equation then shows that Xvb/XvcXlb/XlcThe vapor above an ideal solution is richer than the liquid in the more volatile component. Equations (1) and (2) apply at any pressure where liquid -vapor equilibrium exists, not just at point D. Now let us isothermally lower the pressure below point D, causing more liquid to vaporize. Eventually, WE reach point F in figure, where the last drop of liquid vaporizes. Below F, we have only vapor. For any point or the line between D and F liquid and vapor phases coexist in equilibrium.Q.The equation of the curve obtained by connecting all those points where the vapors of above mixture (all mixtures of different composition are taken) just start forming will bea)b)c)d)Correct answer is option 'A'. Can you explain this answer? has been provided alongside types of Consider two liquids B and C that form an ideal solutlion. We hold the temperature fixed at some value T that is above the freezing points of B and C .We shall plot the systems pressure P and against XB the overall mole fraction of B in the system :Where nbland nbvare the number of moles of B in the liquid and vapor phases, respectively. For a close system xB, is fixed, although nBland nBvmay vary. Let the system be enclosed in a cylinder fitted with a piston and immersed in a constant-temperature bath.To see what the P-versus-xB phase diagram looks like, let us initially set the external pressure on the piston high enough for the system to be entirely liquid (point A in figure) As the pressure is lowered below that at A, the system eventually reaches a pressure where the liquid just begins to vaporizes (point D). At point D, the liquid has composition xlbwhere xlbat D is equal to the overall mole fraction xB since only an infinitesimal amount of liquid has vapourized. What is the composition of the first vapour that comes off ? Raoults law, Pb=xvbPobrelates the vapour-phase mole fractions to the liquid composition as follows:Where Poband Pocare the vapour pressures of pure B and pure C at T, where the systems pressure P equals the sum PB + Pc of the partial pressures, where and the vapor is assumed ideal.Let B be the more volatile component, meaning that PobPocAbove equation then shows that Xvb/XvcXlb/XlcThe vapor above an ideal solution is richer than the liquid in the more volatile component. Equations (1) and (2) apply at any pressure where liquid -vapor equilibrium exists, not just at point D. Now let us isothermally lower the pressure below point D, causing more liquid to vaporize. Eventually, WE reach point F in figure, where the last drop of liquid vaporizes. Below F, we have only vapor. For any point or the line between D and F liquid and vapor phases coexist in equilibrium.Q.The equation of the curve obtained by connecting all those points where the vapors of above mixture (all mixtures of different composition are taken) just start forming will bea)b)c)d)Correct answer is option 'A'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice Consider two liquids B and C that form an ideal solutlion. We hold the temperature fixed at some value T that is above the freezing points of B and C .We shall plot the systems pressure P and against XB the overall mole fraction of B in the system :Where nbland nbvare the number of moles of B in the liquid and vapor phases, respectively. For a close system xB, is fixed, although nBland nBvmay vary. Let the system be enclosed in a cylinder fitted with a piston and immersed in a constant-temperature bath.To see what the P-versus-xB phase diagram looks like, let us initially set the external pressure on the piston high enough for the system to be entirely liquid (point A in figure) As the pressure is lowered below that at A, the system eventually reaches a pressure where the liquid just begins to vaporizes (point D). At point D, the liquid has composition xlbwhere xlbat D is equal to the overall mole fraction xB since only an infinitesimal amount of liquid has vapourized. What is the composition of the first vapour that comes off ? Raoults law, Pb=xvbPobrelates the vapour-phase mole fractions to the liquid composition as follows:Where Poband Pocare the vapour pressures of pure B and pure C at T, where the systems pressure P equals the sum PB + Pc of the partial pressures, where and the vapor is assumed ideal.Let B be the more volatile component, meaning that PobPocAbove equation then shows that Xvb/XvcXlb/XlcThe vapor above an ideal solution is richer than the liquid in the more volatile component. Equations (1) and (2) apply at any pressure where liquid -vapor equilibrium exists, not just at point D. Now let us isothermally lower the pressure below point D, causing more liquid to vaporize. Eventually, WE reach point F in figure, where the last drop of liquid vaporizes. Below F, we have only vapor. For any point or the line between D and F liquid and vapor phases coexist in equilibrium.Q.The equation of the curve obtained by connecting all those points where the vapors of above mixture (all mixtures of different composition are taken) just start forming will bea)b)c)d)Correct answer is option 'A'. Can you explain this answer? tests, examples and also practice JEE tests.

|
Explore Courses for JEE exam
|

|
Suggested Free Tests
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.























