JEE Exam > JEE Questions > Ideal Solution at Fixed TemperatureConsider t...
Start Learning for Free
Ideal Solution at Fixed Temperature
Consider two liquids 'B' and 'C' that form an ideal solution. We hold the temperature fixed at some value T that
is above the freezing points of 'B' and 'C'. We shall plot the system's pressure P against XB, the overall mole
fraction of B in the system :
Consider two liquids 'B' and 'C' that form an ideal solution. We hold the temperature fixed at some value T that
is above the freezing points of 'B' and 'C'. We shall plot the system's pressure P against XB, the overall mole
fraction of B in the system :
Where 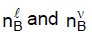 are the number of moles of B in the liquid and vapor phases, respectively. For a closed system XB is fixed, although
are the number of moles of B in the liquid and vapor phases, respectively. For a closed system XB is fixed, although 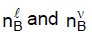 may vary.
may vary.
Let the system be enclosed in a cylinder fitted with a piston and immersed in a constant-temperature bath. To see what the P-versus–XB phase diagram looks like, let us initially set the external pressure on the piston high enough for the system to be entirely liquid (point A in figure) As the pressure is lowered below that at A, the system eventually reaches a pressure where the liquid just begins to vaporizes (point D). At point D, the liquid has composition at D is equal to the overall mole fraction XB since only an infinitesimal amount of liquid has vapourized. What is the composition of the first vapour that comes off ? Raoult's law,
at D is equal to the overall mole fraction XB since only an infinitesimal amount of liquid has vapourized. What is the composition of the first vapour that comes off ? Raoult's law, 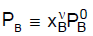 relates the vapour-phase mole fractions to the liquid composition as follows :
relates the vapour-phase mole fractions to the liquid composition as follows :
Let the system be enclosed in a cylinder fitted with a piston and immersed in a constant-temperature bath. To see what the P-versus–XB phase diagram looks like, let us initially set the external pressure on the piston high enough for the system to be entirely liquid (point A in figure) As the pressure is lowered below that at A, the system eventually reaches a pressure where the liquid just begins to vaporizes (point D). At point D, the liquid has composition
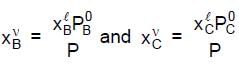 ............(1)
............(1)Where PB0 and PC0 are the vapour pressures of pure 'B' and pure 'C' at T, where the system's pressure P equals the sum PB + PC of the partial pressures, where
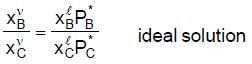 ............(2)
............(2)Let B be the more volatile component, meaning that
Now let us isothermally lower the pressure below point D, causing more liquid to vaporize. Eventually, we
reach point F in figure , where the last drop of liquid vaporizes. Below F, we have only vapour. For any point
on the line between D and F liquid and vapour phases coexist in equilibrium.
Q. Two liquids A and B have the same molecular weight and form an ideal solution. The solution has a vapour pressure of 700 Torrs at 80ºC. It is distilled till 2/3rd of the solution (2/3rd moles out of total moles) is collected as condensate. The composition of the condensate is x'A = 0.75 and that of the residue is x''A= 0.30. If the vapour pressure of the residue at 80ºC is 600 Torrs, find the original composition of the liquid ?
- a)XA = 0.5
- b)XB = 0.6
- c)XA = 0.6
- d)XB = 0.3
Correct answer is option 'C'. Can you explain this answer?
Most Upvoted Answer
Ideal Solution at Fixed TemperatureConsider two liquids B and C that f...
If initially is liquid there are x moles of A and y moles of B then 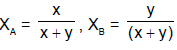
we have
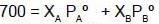 ........(1)
........(1)
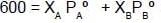 .......(2)
.......(2)
and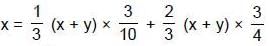
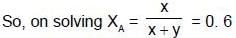
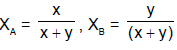
we have
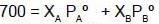 ........(1)
........(1)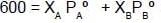 .......(2)
.......(2)and
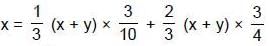
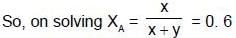

|
Explore Courses for JEE exam
|

|
Question Description
Ideal Solution at Fixed TemperatureConsider two liquids B and C that form an ideal solution. We hold the temperature fixed at some value T thatis above the freezing points of B and C. We shall plot the systems pressure P against XB, the overall molefraction of B in the system :Where are the number of moles of B in the liquid and vapor phases, respectively. For a closed system XB is fixed, although may vary.Let the system be enclosed in a cylinder fitted with a piston and immersed in a constant-temperature bath. To see what the P-versus–XB phase diagram looks like, let us initially set the external pressure on the piston high enough for the system to be entirely liquid (point A in figure) As the pressure is lowered below that at A, the system eventually reaches a pressure where the liquid just begins to vaporizes (point D). At point D, the liquid has composition at D is equal to the overall mole fraction XB since only an infinitesimal amount of liquid has vapourized. What is the composition of the first vapour that comes off ? Raoults law, relates the vapour-phase mole fractions to the liquid composition as follows :............(1)Where PB0 and PC0 are the vapour pressures of pure B and pure C at T, where the systems pressure P equals the sum PB + PC of the partial pressures, where, and the vapour is assumed ideal. ............(2)Let B be the more volatile component, meaning that . Above equation then shows that The vapour above an ideal solution is richer than the liquid in the more volatile component. Equations (1) and (2) apply at any pressure where liquid –vapour equilibrium exists, not just at point D.Now let us isothermally lower the pressure below point D, causing more liquid to vaporize. Eventually, wereach point F in figure , where the last drop of liquid vaporizes. Below F, we have only vapour. For any pointon the line between D and F liquid and vapour phases coexist in equilibrium.Q. Two liquids A and B have the same molecular weight and form an ideal solution. The solution has a vapour pressure of 700 Torrs at 80ºC. It is distilled till 2/3rd of the solution (2/3rd moles out of total moles) is collected as condensate. The composition of the condensate is xA = 0.75 and that of the residue is xA= 0.30. If the vapour pressure of the residue at 80ºC is 600 Torrs, find the original composition of the liquid ?a)XA = 0.5b)XB = 0.6c)XA = 0.6d)XB = 0.3Correct answer is option 'C'. Can you explain this answer? for JEE 2025 is part of JEE preparation. The Question and answers have been prepared according to the JEE exam syllabus. Information about Ideal Solution at Fixed TemperatureConsider two liquids B and C that form an ideal solution. We hold the temperature fixed at some value T thatis above the freezing points of B and C. We shall plot the systems pressure P against XB, the overall molefraction of B in the system :Where are the number of moles of B in the liquid and vapor phases, respectively. For a closed system XB is fixed, although may vary.Let the system be enclosed in a cylinder fitted with a piston and immersed in a constant-temperature bath. To see what the P-versus–XB phase diagram looks like, let us initially set the external pressure on the piston high enough for the system to be entirely liquid (point A in figure) As the pressure is lowered below that at A, the system eventually reaches a pressure where the liquid just begins to vaporizes (point D). At point D, the liquid has composition at D is equal to the overall mole fraction XB since only an infinitesimal amount of liquid has vapourized. What is the composition of the first vapour that comes off ? Raoults law, relates the vapour-phase mole fractions to the liquid composition as follows :............(1)Where PB0 and PC0 are the vapour pressures of pure B and pure C at T, where the systems pressure P equals the sum PB + PC of the partial pressures, where, and the vapour is assumed ideal. ............(2)Let B be the more volatile component, meaning that . Above equation then shows that The vapour above an ideal solution is richer than the liquid in the more volatile component. Equations (1) and (2) apply at any pressure where liquid –vapour equilibrium exists, not just at point D.Now let us isothermally lower the pressure below point D, causing more liquid to vaporize. Eventually, wereach point F in figure , where the last drop of liquid vaporizes. Below F, we have only vapour. For any pointon the line between D and F liquid and vapour phases coexist in equilibrium.Q. Two liquids A and B have the same molecular weight and form an ideal solution. The solution has a vapour pressure of 700 Torrs at 80ºC. It is distilled till 2/3rd of the solution (2/3rd moles out of total moles) is collected as condensate. The composition of the condensate is xA = 0.75 and that of the residue is xA= 0.30. If the vapour pressure of the residue at 80ºC is 600 Torrs, find the original composition of the liquid ?a)XA = 0.5b)XB = 0.6c)XA = 0.6d)XB = 0.3Correct answer is option 'C'. Can you explain this answer? covers all topics & solutions for JEE 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for Ideal Solution at Fixed TemperatureConsider two liquids B and C that form an ideal solution. We hold the temperature fixed at some value T thatis above the freezing points of B and C. We shall plot the systems pressure P against XB, the overall molefraction of B in the system :Where are the number of moles of B in the liquid and vapor phases, respectively. For a closed system XB is fixed, although may vary.Let the system be enclosed in a cylinder fitted with a piston and immersed in a constant-temperature bath. To see what the P-versus–XB phase diagram looks like, let us initially set the external pressure on the piston high enough for the system to be entirely liquid (point A in figure) As the pressure is lowered below that at A, the system eventually reaches a pressure where the liquid just begins to vaporizes (point D). At point D, the liquid has composition at D is equal to the overall mole fraction XB since only an infinitesimal amount of liquid has vapourized. What is the composition of the first vapour that comes off ? Raoults law, relates the vapour-phase mole fractions to the liquid composition as follows :............(1)Where PB0 and PC0 are the vapour pressures of pure B and pure C at T, where the systems pressure P equals the sum PB + PC of the partial pressures, where, and the vapour is assumed ideal. ............(2)Let B be the more volatile component, meaning that . Above equation then shows that The vapour above an ideal solution is richer than the liquid in the more volatile component. Equations (1) and (2) apply at any pressure where liquid –vapour equilibrium exists, not just at point D.Now let us isothermally lower the pressure below point D, causing more liquid to vaporize. Eventually, wereach point F in figure , where the last drop of liquid vaporizes. Below F, we have only vapour. For any pointon the line between D and F liquid and vapour phases coexist in equilibrium.Q. Two liquids A and B have the same molecular weight and form an ideal solution. The solution has a vapour pressure of 700 Torrs at 80ºC. It is distilled till 2/3rd of the solution (2/3rd moles out of total moles) is collected as condensate. The composition of the condensate is xA = 0.75 and that of the residue is xA= 0.30. If the vapour pressure of the residue at 80ºC is 600 Torrs, find the original composition of the liquid ?a)XA = 0.5b)XB = 0.6c)XA = 0.6d)XB = 0.3Correct answer is option 'C'. Can you explain this answer?.
Ideal Solution at Fixed TemperatureConsider two liquids B and C that form an ideal solution. We hold the temperature fixed at some value T thatis above the freezing points of B and C. We shall plot the systems pressure P against XB, the overall molefraction of B in the system :Where are the number of moles of B in the liquid and vapor phases, respectively. For a closed system XB is fixed, although may vary.Let the system be enclosed in a cylinder fitted with a piston and immersed in a constant-temperature bath. To see what the P-versus–XB phase diagram looks like, let us initially set the external pressure on the piston high enough for the system to be entirely liquid (point A in figure) As the pressure is lowered below that at A, the system eventually reaches a pressure where the liquid just begins to vaporizes (point D). At point D, the liquid has composition at D is equal to the overall mole fraction XB since only an infinitesimal amount of liquid has vapourized. What is the composition of the first vapour that comes off ? Raoults law, relates the vapour-phase mole fractions to the liquid composition as follows :............(1)Where PB0 and PC0 are the vapour pressures of pure B and pure C at T, where the systems pressure P equals the sum PB + PC of the partial pressures, where, and the vapour is assumed ideal. ............(2)Let B be the more volatile component, meaning that . Above equation then shows that The vapour above an ideal solution is richer than the liquid in the more volatile component. Equations (1) and (2) apply at any pressure where liquid –vapour equilibrium exists, not just at point D.Now let us isothermally lower the pressure below point D, causing more liquid to vaporize. Eventually, wereach point F in figure , where the last drop of liquid vaporizes. Below F, we have only vapour. For any pointon the line between D and F liquid and vapour phases coexist in equilibrium.Q. Two liquids A and B have the same molecular weight and form an ideal solution. The solution has a vapour pressure of 700 Torrs at 80ºC. It is distilled till 2/3rd of the solution (2/3rd moles out of total moles) is collected as condensate. The composition of the condensate is xA = 0.75 and that of the residue is xA= 0.30. If the vapour pressure of the residue at 80ºC is 600 Torrs, find the original composition of the liquid ?a)XA = 0.5b)XB = 0.6c)XA = 0.6d)XB = 0.3Correct answer is option 'C'. Can you explain this answer? for JEE 2025 is part of JEE preparation. The Question and answers have been prepared according to the JEE exam syllabus. Information about Ideal Solution at Fixed TemperatureConsider two liquids B and C that form an ideal solution. We hold the temperature fixed at some value T thatis above the freezing points of B and C. We shall plot the systems pressure P against XB, the overall molefraction of B in the system :Where are the number of moles of B in the liquid and vapor phases, respectively. For a closed system XB is fixed, although may vary.Let the system be enclosed in a cylinder fitted with a piston and immersed in a constant-temperature bath. To see what the P-versus–XB phase diagram looks like, let us initially set the external pressure on the piston high enough for the system to be entirely liquid (point A in figure) As the pressure is lowered below that at A, the system eventually reaches a pressure where the liquid just begins to vaporizes (point D). At point D, the liquid has composition at D is equal to the overall mole fraction XB since only an infinitesimal amount of liquid has vapourized. What is the composition of the first vapour that comes off ? Raoults law, relates the vapour-phase mole fractions to the liquid composition as follows :............(1)Where PB0 and PC0 are the vapour pressures of pure B and pure C at T, where the systems pressure P equals the sum PB + PC of the partial pressures, where, and the vapour is assumed ideal. ............(2)Let B be the more volatile component, meaning that . Above equation then shows that The vapour above an ideal solution is richer than the liquid in the more volatile component. Equations (1) and (2) apply at any pressure where liquid –vapour equilibrium exists, not just at point D.Now let us isothermally lower the pressure below point D, causing more liquid to vaporize. Eventually, wereach point F in figure , where the last drop of liquid vaporizes. Below F, we have only vapour. For any pointon the line between D and F liquid and vapour phases coexist in equilibrium.Q. Two liquids A and B have the same molecular weight and form an ideal solution. The solution has a vapour pressure of 700 Torrs at 80ºC. It is distilled till 2/3rd of the solution (2/3rd moles out of total moles) is collected as condensate. The composition of the condensate is xA = 0.75 and that of the residue is xA= 0.30. If the vapour pressure of the residue at 80ºC is 600 Torrs, find the original composition of the liquid ?a)XA = 0.5b)XB = 0.6c)XA = 0.6d)XB = 0.3Correct answer is option 'C'. Can you explain this answer? covers all topics & solutions for JEE 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for Ideal Solution at Fixed TemperatureConsider two liquids B and C that form an ideal solution. We hold the temperature fixed at some value T thatis above the freezing points of B and C. We shall plot the systems pressure P against XB, the overall molefraction of B in the system :Where are the number of moles of B in the liquid and vapor phases, respectively. For a closed system XB is fixed, although may vary.Let the system be enclosed in a cylinder fitted with a piston and immersed in a constant-temperature bath. To see what the P-versus–XB phase diagram looks like, let us initially set the external pressure on the piston high enough for the system to be entirely liquid (point A in figure) As the pressure is lowered below that at A, the system eventually reaches a pressure where the liquid just begins to vaporizes (point D). At point D, the liquid has composition at D is equal to the overall mole fraction XB since only an infinitesimal amount of liquid has vapourized. What is the composition of the first vapour that comes off ? Raoults law, relates the vapour-phase mole fractions to the liquid composition as follows :............(1)Where PB0 and PC0 are the vapour pressures of pure B and pure C at T, where the systems pressure P equals the sum PB + PC of the partial pressures, where, and the vapour is assumed ideal. ............(2)Let B be the more volatile component, meaning that . Above equation then shows that The vapour above an ideal solution is richer than the liquid in the more volatile component. Equations (1) and (2) apply at any pressure where liquid –vapour equilibrium exists, not just at point D.Now let us isothermally lower the pressure below point D, causing more liquid to vaporize. Eventually, wereach point F in figure , where the last drop of liquid vaporizes. Below F, we have only vapour. For any pointon the line between D and F liquid and vapour phases coexist in equilibrium.Q. Two liquids A and B have the same molecular weight and form an ideal solution. The solution has a vapour pressure of 700 Torrs at 80ºC. It is distilled till 2/3rd of the solution (2/3rd moles out of total moles) is collected as condensate. The composition of the condensate is xA = 0.75 and that of the residue is xA= 0.30. If the vapour pressure of the residue at 80ºC is 600 Torrs, find the original composition of the liquid ?a)XA = 0.5b)XB = 0.6c)XA = 0.6d)XB = 0.3Correct answer is option 'C'. Can you explain this answer?.
Solutions for Ideal Solution at Fixed TemperatureConsider two liquids B and C that form an ideal solution. We hold the temperature fixed at some value T thatis above the freezing points of B and C. We shall plot the systems pressure P against XB, the overall molefraction of B in the system :Where are the number of moles of B in the liquid and vapor phases, respectively. For a closed system XB is fixed, although may vary.Let the system be enclosed in a cylinder fitted with a piston and immersed in a constant-temperature bath. To see what the P-versus–XB phase diagram looks like, let us initially set the external pressure on the piston high enough for the system to be entirely liquid (point A in figure) As the pressure is lowered below that at A, the system eventually reaches a pressure where the liquid just begins to vaporizes (point D). At point D, the liquid has composition at D is equal to the overall mole fraction XB since only an infinitesimal amount of liquid has vapourized. What is the composition of the first vapour that comes off ? Raoults law, relates the vapour-phase mole fractions to the liquid composition as follows :............(1)Where PB0 and PC0 are the vapour pressures of pure B and pure C at T, where the systems pressure P equals the sum PB + PC of the partial pressures, where, and the vapour is assumed ideal. ............(2)Let B be the more volatile component, meaning that . Above equation then shows that The vapour above an ideal solution is richer than the liquid in the more volatile component. Equations (1) and (2) apply at any pressure where liquid –vapour equilibrium exists, not just at point D.Now let us isothermally lower the pressure below point D, causing more liquid to vaporize. Eventually, wereach point F in figure , where the last drop of liquid vaporizes. Below F, we have only vapour. For any pointon the line between D and F liquid and vapour phases coexist in equilibrium.Q. Two liquids A and B have the same molecular weight and form an ideal solution. The solution has a vapour pressure of 700 Torrs at 80ºC. It is distilled till 2/3rd of the solution (2/3rd moles out of total moles) is collected as condensate. The composition of the condensate is xA = 0.75 and that of the residue is xA= 0.30. If the vapour pressure of the residue at 80ºC is 600 Torrs, find the original composition of the liquid ?a)XA = 0.5b)XB = 0.6c)XA = 0.6d)XB = 0.3Correct answer is option 'C'. Can you explain this answer? in English & in Hindi are available as part of our courses for JEE.
Download more important topics, notes, lectures and mock test series for JEE Exam by signing up for free.
Here you can find the meaning of Ideal Solution at Fixed TemperatureConsider two liquids B and C that form an ideal solution. We hold the temperature fixed at some value T thatis above the freezing points of B and C. We shall plot the systems pressure P against XB, the overall molefraction of B in the system :Where are the number of moles of B in the liquid and vapor phases, respectively. For a closed system XB is fixed, although may vary.Let the system be enclosed in a cylinder fitted with a piston and immersed in a constant-temperature bath. To see what the P-versus–XB phase diagram looks like, let us initially set the external pressure on the piston high enough for the system to be entirely liquid (point A in figure) As the pressure is lowered below that at A, the system eventually reaches a pressure where the liquid just begins to vaporizes (point D). At point D, the liquid has composition at D is equal to the overall mole fraction XB since only an infinitesimal amount of liquid has vapourized. What is the composition of the first vapour that comes off ? Raoults law, relates the vapour-phase mole fractions to the liquid composition as follows :............(1)Where PB0 and PC0 are the vapour pressures of pure B and pure C at T, where the systems pressure P equals the sum PB + PC of the partial pressures, where, and the vapour is assumed ideal. ............(2)Let B be the more volatile component, meaning that . Above equation then shows that The vapour above an ideal solution is richer than the liquid in the more volatile component. Equations (1) and (2) apply at any pressure where liquid –vapour equilibrium exists, not just at point D.Now let us isothermally lower the pressure below point D, causing more liquid to vaporize. Eventually, wereach point F in figure , where the last drop of liquid vaporizes. Below F, we have only vapour. For any pointon the line between D and F liquid and vapour phases coexist in equilibrium.Q. Two liquids A and B have the same molecular weight and form an ideal solution. The solution has a vapour pressure of 700 Torrs at 80ºC. It is distilled till 2/3rd of the solution (2/3rd moles out of total moles) is collected as condensate. The composition of the condensate is xA = 0.75 and that of the residue is xA= 0.30. If the vapour pressure of the residue at 80ºC is 600 Torrs, find the original composition of the liquid ?a)XA = 0.5b)XB = 0.6c)XA = 0.6d)XB = 0.3Correct answer is option 'C'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
Ideal Solution at Fixed TemperatureConsider two liquids B and C that form an ideal solution. We hold the temperature fixed at some value T thatis above the freezing points of B and C. We shall plot the systems pressure P against XB, the overall molefraction of B in the system :Where are the number of moles of B in the liquid and vapor phases, respectively. For a closed system XB is fixed, although may vary.Let the system be enclosed in a cylinder fitted with a piston and immersed in a constant-temperature bath. To see what the P-versus–XB phase diagram looks like, let us initially set the external pressure on the piston high enough for the system to be entirely liquid (point A in figure) As the pressure is lowered below that at A, the system eventually reaches a pressure where the liquid just begins to vaporizes (point D). At point D, the liquid has composition at D is equal to the overall mole fraction XB since only an infinitesimal amount of liquid has vapourized. What is the composition of the first vapour that comes off ? Raoults law, relates the vapour-phase mole fractions to the liquid composition as follows :............(1)Where PB0 and PC0 are the vapour pressures of pure B and pure C at T, where the systems pressure P equals the sum PB + PC of the partial pressures, where, and the vapour is assumed ideal. ............(2)Let B be the more volatile component, meaning that . Above equation then shows that The vapour above an ideal solution is richer than the liquid in the more volatile component. Equations (1) and (2) apply at any pressure where liquid –vapour equilibrium exists, not just at point D.Now let us isothermally lower the pressure below point D, causing more liquid to vaporize. Eventually, wereach point F in figure , where the last drop of liquid vaporizes. Below F, we have only vapour. For any pointon the line between D and F liquid and vapour phases coexist in equilibrium.Q. Two liquids A and B have the same molecular weight and form an ideal solution. The solution has a vapour pressure of 700 Torrs at 80ºC. It is distilled till 2/3rd of the solution (2/3rd moles out of total moles) is collected as condensate. The composition of the condensate is xA = 0.75 and that of the residue is xA= 0.30. If the vapour pressure of the residue at 80ºC is 600 Torrs, find the original composition of the liquid ?a)XA = 0.5b)XB = 0.6c)XA = 0.6d)XB = 0.3Correct answer is option 'C'. Can you explain this answer?, a detailed solution for Ideal Solution at Fixed TemperatureConsider two liquids B and C that form an ideal solution. We hold the temperature fixed at some value T thatis above the freezing points of B and C. We shall plot the systems pressure P against XB, the overall molefraction of B in the system :Where are the number of moles of B in the liquid and vapor phases, respectively. For a closed system XB is fixed, although may vary.Let the system be enclosed in a cylinder fitted with a piston and immersed in a constant-temperature bath. To see what the P-versus–XB phase diagram looks like, let us initially set the external pressure on the piston high enough for the system to be entirely liquid (point A in figure) As the pressure is lowered below that at A, the system eventually reaches a pressure where the liquid just begins to vaporizes (point D). At point D, the liquid has composition at D is equal to the overall mole fraction XB since only an infinitesimal amount of liquid has vapourized. What is the composition of the first vapour that comes off ? Raoults law, relates the vapour-phase mole fractions to the liquid composition as follows :............(1)Where PB0 and PC0 are the vapour pressures of pure B and pure C at T, where the systems pressure P equals the sum PB + PC of the partial pressures, where, and the vapour is assumed ideal. ............(2)Let B be the more volatile component, meaning that . Above equation then shows that The vapour above an ideal solution is richer than the liquid in the more volatile component. Equations (1) and (2) apply at any pressure where liquid –vapour equilibrium exists, not just at point D.Now let us isothermally lower the pressure below point D, causing more liquid to vaporize. Eventually, wereach point F in figure , where the last drop of liquid vaporizes. Below F, we have only vapour. For any pointon the line between D and F liquid and vapour phases coexist in equilibrium.Q. Two liquids A and B have the same molecular weight and form an ideal solution. The solution has a vapour pressure of 700 Torrs at 80ºC. It is distilled till 2/3rd of the solution (2/3rd moles out of total moles) is collected as condensate. The composition of the condensate is xA = 0.75 and that of the residue is xA= 0.30. If the vapour pressure of the residue at 80ºC is 600 Torrs, find the original composition of the liquid ?a)XA = 0.5b)XB = 0.6c)XA = 0.6d)XB = 0.3Correct answer is option 'C'. Can you explain this answer? has been provided alongside types of Ideal Solution at Fixed TemperatureConsider two liquids B and C that form an ideal solution. We hold the temperature fixed at some value T thatis above the freezing points of B and C. We shall plot the systems pressure P against XB, the overall molefraction of B in the system :Where are the number of moles of B in the liquid and vapor phases, respectively. For a closed system XB is fixed, although may vary.Let the system be enclosed in a cylinder fitted with a piston and immersed in a constant-temperature bath. To see what the P-versus–XB phase diagram looks like, let us initially set the external pressure on the piston high enough for the system to be entirely liquid (point A in figure) As the pressure is lowered below that at A, the system eventually reaches a pressure where the liquid just begins to vaporizes (point D). At point D, the liquid has composition at D is equal to the overall mole fraction XB since only an infinitesimal amount of liquid has vapourized. What is the composition of the first vapour that comes off ? Raoults law, relates the vapour-phase mole fractions to the liquid composition as follows :............(1)Where PB0 and PC0 are the vapour pressures of pure B and pure C at T, where the systems pressure P equals the sum PB + PC of the partial pressures, where, and the vapour is assumed ideal. ............(2)Let B be the more volatile component, meaning that . Above equation then shows that The vapour above an ideal solution is richer than the liquid in the more volatile component. Equations (1) and (2) apply at any pressure where liquid –vapour equilibrium exists, not just at point D.Now let us isothermally lower the pressure below point D, causing more liquid to vaporize. Eventually, wereach point F in figure , where the last drop of liquid vaporizes. Below F, we have only vapour. For any pointon the line between D and F liquid and vapour phases coexist in equilibrium.Q. Two liquids A and B have the same molecular weight and form an ideal solution. The solution has a vapour pressure of 700 Torrs at 80ºC. It is distilled till 2/3rd of the solution (2/3rd moles out of total moles) is collected as condensate. The composition of the condensate is xA = 0.75 and that of the residue is xA= 0.30. If the vapour pressure of the residue at 80ºC is 600 Torrs, find the original composition of the liquid ?a)XA = 0.5b)XB = 0.6c)XA = 0.6d)XB = 0.3Correct answer is option 'C'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice Ideal Solution at Fixed TemperatureConsider two liquids B and C that form an ideal solution. We hold the temperature fixed at some value T thatis above the freezing points of B and C. We shall plot the systems pressure P against XB, the overall molefraction of B in the system :Where are the number of moles of B in the liquid and vapor phases, respectively. For a closed system XB is fixed, although may vary.Let the system be enclosed in a cylinder fitted with a piston and immersed in a constant-temperature bath. To see what the P-versus–XB phase diagram looks like, let us initially set the external pressure on the piston high enough for the system to be entirely liquid (point A in figure) As the pressure is lowered below that at A, the system eventually reaches a pressure where the liquid just begins to vaporizes (point D). At point D, the liquid has composition at D is equal to the overall mole fraction XB since only an infinitesimal amount of liquid has vapourized. What is the composition of the first vapour that comes off ? Raoults law, relates the vapour-phase mole fractions to the liquid composition as follows :............(1)Where PB0 and PC0 are the vapour pressures of pure B and pure C at T, where the systems pressure P equals the sum PB + PC of the partial pressures, where, and the vapour is assumed ideal. ............(2)Let B be the more volatile component, meaning that . Above equation then shows that The vapour above an ideal solution is richer than the liquid in the more volatile component. Equations (1) and (2) apply at any pressure where liquid –vapour equilibrium exists, not just at point D.Now let us isothermally lower the pressure below point D, causing more liquid to vaporize. Eventually, wereach point F in figure , where the last drop of liquid vaporizes. Below F, we have only vapour. For any pointon the line between D and F liquid and vapour phases coexist in equilibrium.Q. Two liquids A and B have the same molecular weight and form an ideal solution. The solution has a vapour pressure of 700 Torrs at 80ºC. It is distilled till 2/3rd of the solution (2/3rd moles out of total moles) is collected as condensate. The composition of the condensate is xA = 0.75 and that of the residue is xA= 0.30. If the vapour pressure of the residue at 80ºC is 600 Torrs, find the original composition of the liquid ?a)XA = 0.5b)XB = 0.6c)XA = 0.6d)XB = 0.3Correct answer is option 'C'. Can you explain this answer? tests, examples and also practice JEE tests.

|
Explore Courses for JEE exam
|

|
Signup to solve all Doubts
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.



















