Class 9 Exam > Class 9 Questions > The bisectors of the angles of a Parallelogra...
Start Learning for Free
The bisectors of the angles of a Parallelogram enclose a
- a)Rhombus
- b)Square
- c)Parallelogram
- d)Rectangle
Correct answer is option 'D'. Can you explain this answer?
Verified Answer
The bisectors of the angles of a Parallelogram enclose aa)Rhombusb)Squ...
We have ABCD, a parallelogram given below:
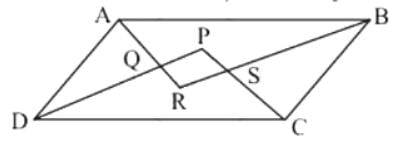
Therefore, we have AB || BC

Therefore, we have AB || BC
Now, AD || BC and transversal AB intersects them at A and B respectively. Therefore,
Sum of consecutive interior angle is supplementary. That is;
∠A + ∠B = 180°
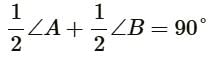
∠A + ∠B = 180°
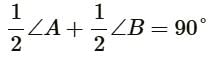
We have AR and BR as bisectors of ∠A and ∠B respectively.
∠RAB +∠RBA = 90° …… (i)
Now, in ΔABR, by angle sum property of a triangle, we get:
∠RAB + ∠RBA +∠ARB = 180°
From equation (i), we get:
90° + ∠ARB = 180°
∠ARB = 90°
Similarly, we can prove that ∠DPC = 90° .
Now, AB || DC and transversal ADintersects them at A and D respectively. Therefore,
Sum of consecutive interior angle is supplementary. That is;
∠A + ∠D = 180°


We have AR and DP as bisectors of ∠A and ∠D respectively.
∠DAR + ∠ADP = 90° …… (ii)
Now, in ΔADR, by angle sum property of a triangle, we get:
∠DAR + ∠ADP + ∠AQD = 180°
From equation (i), we get:
90° +∠AQD = 180°
∠AQD = 90°
We know that ∠AQD and ∠PQR are vertically opposite angles, thus,
∠PQR = 90°
Similarly, we can prove that ∠PSR = 90° .
Therefore, PQRS is a rectangle.
Hence, the correct choice is (d).
Most Upvoted Answer
The bisectors of the angles of a Parallelogram enclose aa)Rhombusb)Squ...
The ans is option d the bisectors of the angles of a parallelogram enclose a rectangle .
Free Test
FREE
| Start Free Test |
Community Answer
The bisectors of the angles of a Parallelogram enclose aa)Rhombusb)Squ...
Bisectors of the angles of a parallelogram enclose a rectangle.
Explanation:
A parallelogram is a quadrilateral with opposite sides that are parallel and equal in length. The opposite angles of a parallelogram are also equal.
When we draw the bisectors of the angles of a parallelogram, we divide each angle into two equal parts.
Proof:
Let's consider a parallelogram ABCD.
1. Draw the bisector of angle A:
- Draw a line that passes through the vertex A and divides angle A into two equal parts. Let this line intersect the opposite side DC at point E.
2. Draw the bisector of angle B:
- Draw a line that passes through the vertex B and divides angle B into two equal parts. Let this line intersect the opposite side AD at point F.
3. Draw the bisector of angle C:
- Draw a line that passes through the vertex C and divides angle C into two equal parts. Let this line intersect the opposite side AB at point G.
4. Draw the bisector of angle D:
- Draw a line that passes through the vertex D and divides angle D into two equal parts. Let this line intersect the opposite side BC at point H.
Properties of the bisectors:
- The bisector of angle A divides the opposite side DC into two equal parts, DE and EC.
- The bisector of angle B divides the opposite side AD into two equal parts, AF and FD.
- The bisector of angle C divides the opposite side AB into two equal parts, AG and GB.
- The bisector of angle D divides the opposite side BC into two equal parts, BH and HC.
Analysis:
By drawing the bisectors of the angles of the parallelogram, we can observe the following:
- The bisectors of angles A and C are parallel to each other, as are the bisectors of angles B and D.
- The bisectors of angles A and C intersect at point G, and the bisectors of angles B and D intersect at point F.
- The bisectors of angles A and D intersect at point E, and the bisectors of angles B and C intersect at point H.
Conclusion:
From the properties and analysis, we can conclude that the bisectors of the angles of a parallelogram enclose a rectangle. In a rectangle, opposite sides are parallel and equal in length, and all angles are right angles. Therefore, the correct answer is option 'D' - Rectangle.
Explanation:
A parallelogram is a quadrilateral with opposite sides that are parallel and equal in length. The opposite angles of a parallelogram are also equal.
When we draw the bisectors of the angles of a parallelogram, we divide each angle into two equal parts.
Proof:
Let's consider a parallelogram ABCD.
1. Draw the bisector of angle A:
- Draw a line that passes through the vertex A and divides angle A into two equal parts. Let this line intersect the opposite side DC at point E.
2. Draw the bisector of angle B:
- Draw a line that passes through the vertex B and divides angle B into two equal parts. Let this line intersect the opposite side AD at point F.
3. Draw the bisector of angle C:
- Draw a line that passes through the vertex C and divides angle C into two equal parts. Let this line intersect the opposite side AB at point G.
4. Draw the bisector of angle D:
- Draw a line that passes through the vertex D and divides angle D into two equal parts. Let this line intersect the opposite side BC at point H.
Properties of the bisectors:
- The bisector of angle A divides the opposite side DC into two equal parts, DE and EC.
- The bisector of angle B divides the opposite side AD into two equal parts, AF and FD.
- The bisector of angle C divides the opposite side AB into two equal parts, AG and GB.
- The bisector of angle D divides the opposite side BC into two equal parts, BH and HC.
Analysis:
By drawing the bisectors of the angles of the parallelogram, we can observe the following:
- The bisectors of angles A and C are parallel to each other, as are the bisectors of angles B and D.
- The bisectors of angles A and C intersect at point G, and the bisectors of angles B and D intersect at point F.
- The bisectors of angles A and D intersect at point E, and the bisectors of angles B and C intersect at point H.
Conclusion:
From the properties and analysis, we can conclude that the bisectors of the angles of a parallelogram enclose a rectangle. In a rectangle, opposite sides are parallel and equal in length, and all angles are right angles. Therefore, the correct answer is option 'D' - Rectangle.

|
Explore Courses for Class 9 exam
|

|
Question Description
The bisectors of the angles of a Parallelogram enclose aa)Rhombusb)Squarec)Parallelogramd)RectangleCorrect answer is option 'D'. Can you explain this answer? for Class 9 2025 is part of Class 9 preparation. The Question and answers have been prepared according to the Class 9 exam syllabus. Information about The bisectors of the angles of a Parallelogram enclose aa)Rhombusb)Squarec)Parallelogramd)RectangleCorrect answer is option 'D'. Can you explain this answer? covers all topics & solutions for Class 9 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for The bisectors of the angles of a Parallelogram enclose aa)Rhombusb)Squarec)Parallelogramd)RectangleCorrect answer is option 'D'. Can you explain this answer?.
The bisectors of the angles of a Parallelogram enclose aa)Rhombusb)Squarec)Parallelogramd)RectangleCorrect answer is option 'D'. Can you explain this answer? for Class 9 2025 is part of Class 9 preparation. The Question and answers have been prepared according to the Class 9 exam syllabus. Information about The bisectors of the angles of a Parallelogram enclose aa)Rhombusb)Squarec)Parallelogramd)RectangleCorrect answer is option 'D'. Can you explain this answer? covers all topics & solutions for Class 9 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for The bisectors of the angles of a Parallelogram enclose aa)Rhombusb)Squarec)Parallelogramd)RectangleCorrect answer is option 'D'. Can you explain this answer?.
Solutions for The bisectors of the angles of a Parallelogram enclose aa)Rhombusb)Squarec)Parallelogramd)RectangleCorrect answer is option 'D'. Can you explain this answer? in English & in Hindi are available as part of our courses for Class 9.
Download more important topics, notes, lectures and mock test series for Class 9 Exam by signing up for free.
Here you can find the meaning of The bisectors of the angles of a Parallelogram enclose aa)Rhombusb)Squarec)Parallelogramd)RectangleCorrect answer is option 'D'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
The bisectors of the angles of a Parallelogram enclose aa)Rhombusb)Squarec)Parallelogramd)RectangleCorrect answer is option 'D'. Can you explain this answer?, a detailed solution for The bisectors of the angles of a Parallelogram enclose aa)Rhombusb)Squarec)Parallelogramd)RectangleCorrect answer is option 'D'. Can you explain this answer? has been provided alongside types of The bisectors of the angles of a Parallelogram enclose aa)Rhombusb)Squarec)Parallelogramd)RectangleCorrect answer is option 'D'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice The bisectors of the angles of a Parallelogram enclose aa)Rhombusb)Squarec)Parallelogramd)RectangleCorrect answer is option 'D'. Can you explain this answer? tests, examples and also practice Class 9 tests.

|
Explore Courses for Class 9 exam
|

|
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.


















