Electrical Engineering (EE) Exam > Electrical Engineering (EE) Questions > The characteristic impedance of a distortionl...
Start Learning for Free
The characteristic impedance of a distortionless line is
- a)inductive
- b)capacitive
- c)complex
- d)real
Correct answer is option 'D'. Can you explain this answer?
Verified Answer
The characteristic impedance of a distortionless line isa)inductiveb)c...
Characteristic impedance,
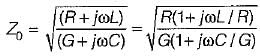
or,
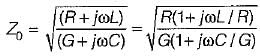
or,
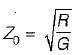
(Since L/R = C/G for a distortionless line)
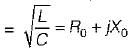
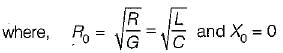
Hence, characteristic impedance of a distortionless line is purely real.
Most Upvoted Answer
The characteristic impedance of a distortionless line isa)inductiveb)c...
Characteristic Impedance of a Distortionless Line
The characteristic impedance of a distortionless line refers to the impedance that a transmission line presents to a signal when it is terminated in its characteristic impedance. It is an important parameter in the design and operation of transmission lines, as it determines the behavior of the line and the efficient transfer of signals.
Definition of Characteristic Impedance
The characteristic impedance (Z0) of a transmission line is defined as the ratio of the voltage wave to the current wave at any point along the line. It represents the distributed impedance of the line and is independent of its length.
Distortionless Line
A distortionless line is a transmission line that maintains the shape of the signal waveform without any distortion. This means that the signal travels along the line without any changes in its amplitude, phase, or shape.
Real Characteristic Impedance
The characteristic impedance of a distortionless line is a real value. This means that it does not have any imaginary component (reactance). The real characteristic impedance is a result of the distributed resistance and inductance of the line. It represents the impedance that a signal would encounter if it were terminated in a purely resistive load equal to the characteristic impedance.
Reason for Real Characteristic Impedance
The real characteristic impedance of a distortionless line is a consequence of the balanced distribution of resistance and inductance along the line. The resistance is responsible for dissipating power, while the inductance helps in maintaining the shape of the signal.
Since the characteristic impedance is real, it implies that the line is neither purely inductive nor capacitive. If the characteristic impedance were inductive or capacitive, it would introduce phase shifts and distort the signal waveform, which is not desirable in a distortionless line.
In practice, the characteristic impedance of a distortionless line is usually a purely resistive value, typically around 50 or 75 ohms for coaxial cables or around 100 ohms for twisted pair cables. These values are carefully chosen to match the impedance of the devices connected to the transmission line, ensuring efficient power transfer and minimizing signal reflections.
Conclusion
The characteristic impedance of a distortionless line is a real value, representing the distributed resistance and inductance of the line. It is neither inductive nor capacitive, as it does not introduce phase shifts or distort the signal waveform. The real characteristic impedance is crucial for maintaining signal integrity and efficient power transfer in transmission lines.
The characteristic impedance of a distortionless line refers to the impedance that a transmission line presents to a signal when it is terminated in its characteristic impedance. It is an important parameter in the design and operation of transmission lines, as it determines the behavior of the line and the efficient transfer of signals.
Definition of Characteristic Impedance
The characteristic impedance (Z0) of a transmission line is defined as the ratio of the voltage wave to the current wave at any point along the line. It represents the distributed impedance of the line and is independent of its length.
Distortionless Line
A distortionless line is a transmission line that maintains the shape of the signal waveform without any distortion. This means that the signal travels along the line without any changes in its amplitude, phase, or shape.
Real Characteristic Impedance
The characteristic impedance of a distortionless line is a real value. This means that it does not have any imaginary component (reactance). The real characteristic impedance is a result of the distributed resistance and inductance of the line. It represents the impedance that a signal would encounter if it were terminated in a purely resistive load equal to the characteristic impedance.
Reason for Real Characteristic Impedance
The real characteristic impedance of a distortionless line is a consequence of the balanced distribution of resistance and inductance along the line. The resistance is responsible for dissipating power, while the inductance helps in maintaining the shape of the signal.
Since the characteristic impedance is real, it implies that the line is neither purely inductive nor capacitive. If the characteristic impedance were inductive or capacitive, it would introduce phase shifts and distort the signal waveform, which is not desirable in a distortionless line.
In practice, the characteristic impedance of a distortionless line is usually a purely resistive value, typically around 50 or 75 ohms for coaxial cables or around 100 ohms for twisted pair cables. These values are carefully chosen to match the impedance of the devices connected to the transmission line, ensuring efficient power transfer and minimizing signal reflections.
Conclusion
The characteristic impedance of a distortionless line is a real value, representing the distributed resistance and inductance of the line. It is neither inductive nor capacitive, as it does not introduce phase shifts or distort the signal waveform. The real characteristic impedance is crucial for maintaining signal integrity and efficient power transfer in transmission lines.

|
Explore Courses for Electrical Engineering (EE) exam
|

|
Question Description
The characteristic impedance of a distortionless line isa)inductiveb)capacitivec)complexd)realCorrect answer is option 'D'. Can you explain this answer? for Electrical Engineering (EE) 2025 is part of Electrical Engineering (EE) preparation. The Question and answers have been prepared according to the Electrical Engineering (EE) exam syllabus. Information about The characteristic impedance of a distortionless line isa)inductiveb)capacitivec)complexd)realCorrect answer is option 'D'. Can you explain this answer? covers all topics & solutions for Electrical Engineering (EE) 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for The characteristic impedance of a distortionless line isa)inductiveb)capacitivec)complexd)realCorrect answer is option 'D'. Can you explain this answer?.
The characteristic impedance of a distortionless line isa)inductiveb)capacitivec)complexd)realCorrect answer is option 'D'. Can you explain this answer? for Electrical Engineering (EE) 2025 is part of Electrical Engineering (EE) preparation. The Question and answers have been prepared according to the Electrical Engineering (EE) exam syllabus. Information about The characteristic impedance of a distortionless line isa)inductiveb)capacitivec)complexd)realCorrect answer is option 'D'. Can you explain this answer? covers all topics & solutions for Electrical Engineering (EE) 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for The characteristic impedance of a distortionless line isa)inductiveb)capacitivec)complexd)realCorrect answer is option 'D'. Can you explain this answer?.
Solutions for The characteristic impedance of a distortionless line isa)inductiveb)capacitivec)complexd)realCorrect answer is option 'D'. Can you explain this answer? in English & in Hindi are available as part of our courses for Electrical Engineering (EE).
Download more important topics, notes, lectures and mock test series for Electrical Engineering (EE) Exam by signing up for free.
Here you can find the meaning of The characteristic impedance of a distortionless line isa)inductiveb)capacitivec)complexd)realCorrect answer is option 'D'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
The characteristic impedance of a distortionless line isa)inductiveb)capacitivec)complexd)realCorrect answer is option 'D'. Can you explain this answer?, a detailed solution for The characteristic impedance of a distortionless line isa)inductiveb)capacitivec)complexd)realCorrect answer is option 'D'. Can you explain this answer? has been provided alongside types of The characteristic impedance of a distortionless line isa)inductiveb)capacitivec)complexd)realCorrect answer is option 'D'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice The characteristic impedance of a distortionless line isa)inductiveb)capacitivec)complexd)realCorrect answer is option 'D'. Can you explain this answer? tests, examples and also practice Electrical Engineering (EE) tests.

|
Explore Courses for Electrical Engineering (EE) exam
|

|
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.























