Mechanical Engineering Exam > Mechanical Engineering Questions > The ratio of thermal conductivity to electric...
Start Learning for Free
The ratio of thermal conductivity to electrical conductivity is equal to
- a)Prandtl number
- b)Schmidt number
- c)Lorentz number
- d)Lewis number
Correct answer is option 'C'. Can you explain this answer?
Verified Answer
The ratio of thermal conductivity to electrical conductivity is equal ...
The ratio of thermal conductivity to electrical conductivity is always constant for all the conductors at the given temperature. This is know as Wideman and Frange law.
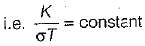
The constant is known as Lorentz number (Lo) whose value is equal to 2.045 x 10-8 W/μK2.
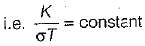
The constant is known as Lorentz number (Lo) whose value is equal to 2.045 x 10-8 W/μK2.
Most Upvoted Answer
The ratio of thermal conductivity to electrical conductivity is equal ...
Explanation:
The ratio of thermal conductivity (k) to electrical conductivity (σ) is represented by a dimensionless number known as the Lorentz number (L). The Lorentz number relates the ability of a material to conduct heat to its ability to conduct electricity. It is named after the Dutch physicist Hendrik Lorentz.
Lorentz number (L) is defined as:
L = (k/σ) * (T/μ)
Where:
- k is the thermal conductivity of the material
- σ is the electrical conductivity of the material
- T is the absolute temperature
- μ is the chemical potential of the charge carriers
Interpretation of Lorentz number:
The Lorentz number provides a measure of the scattering of charge carriers in a material. It expresses the relationship between the transport properties of heat and electricity. A higher Lorentz number indicates that the material is a better conductor of heat compared to electricity, while a lower Lorentz number indicates the opposite.
Significance of Lorentz number:
The Lorentz number is particularly useful in the study of metals and other conductive materials. It helps in understanding the behavior of charge carriers and their interactions with lattice vibrations (phonons) and impurities. By comparing the Lorentz number of different materials, scientists and engineers can gain insights into their thermal and electrical transport properties.
Relation to other dimensionless numbers:
The Lorentz number is related to other dimensionless numbers used in fluid dynamics and heat transfer. For example:
- The Prandtl number (Pr) is the ratio of momentum diffusivity to thermal diffusivity and is defined as Pr = ν/α, where ν is the kinematic viscosity and α is the thermal diffusivity. The Prandtl number is used to characterize the flow and heat transfer behavior of fluids.
- The Schmidt number (Sc) is the ratio of momentum diffusivity to mass diffusivity and is defined as Sc = ν/D, where D is the mass diffusivity. The Schmidt number is used to characterize the mass transfer behavior in fluids.
While the Prandtl and Schmidt numbers are specific to fluid dynamics, the Lorentz number is specifically related to the ratio of thermal conductivity to electrical conductivity in materials. Therefore, the correct answer to the given question is option 'C' - Lorentz number.
The ratio of thermal conductivity (k) to electrical conductivity (σ) is represented by a dimensionless number known as the Lorentz number (L). The Lorentz number relates the ability of a material to conduct heat to its ability to conduct electricity. It is named after the Dutch physicist Hendrik Lorentz.
Lorentz number (L) is defined as:
L = (k/σ) * (T/μ)
Where:
- k is the thermal conductivity of the material
- σ is the electrical conductivity of the material
- T is the absolute temperature
- μ is the chemical potential of the charge carriers
Interpretation of Lorentz number:
The Lorentz number provides a measure of the scattering of charge carriers in a material. It expresses the relationship between the transport properties of heat and electricity. A higher Lorentz number indicates that the material is a better conductor of heat compared to electricity, while a lower Lorentz number indicates the opposite.
Significance of Lorentz number:
The Lorentz number is particularly useful in the study of metals and other conductive materials. It helps in understanding the behavior of charge carriers and their interactions with lattice vibrations (phonons) and impurities. By comparing the Lorentz number of different materials, scientists and engineers can gain insights into their thermal and electrical transport properties.
Relation to other dimensionless numbers:
The Lorentz number is related to other dimensionless numbers used in fluid dynamics and heat transfer. For example:
- The Prandtl number (Pr) is the ratio of momentum diffusivity to thermal diffusivity and is defined as Pr = ν/α, where ν is the kinematic viscosity and α is the thermal diffusivity. The Prandtl number is used to characterize the flow and heat transfer behavior of fluids.
- The Schmidt number (Sc) is the ratio of momentum diffusivity to mass diffusivity and is defined as Sc = ν/D, where D is the mass diffusivity. The Schmidt number is used to characterize the mass transfer behavior in fluids.
While the Prandtl and Schmidt numbers are specific to fluid dynamics, the Lorentz number is specifically related to the ratio of thermal conductivity to electrical conductivity in materials. Therefore, the correct answer to the given question is option 'C' - Lorentz number.

|
Explore Courses for Mechanical Engineering exam
|

|
Question Description
The ratio of thermal conductivity to electrical conductivity is equal toa)Prandtl numberb)Schmidt numberc)Lorentz numberd)Lewis numberCorrect answer is option 'C'. Can you explain this answer? for Mechanical Engineering 2025 is part of Mechanical Engineering preparation. The Question and answers have been prepared according to the Mechanical Engineering exam syllabus. Information about The ratio of thermal conductivity to electrical conductivity is equal toa)Prandtl numberb)Schmidt numberc)Lorentz numberd)Lewis numberCorrect answer is option 'C'. Can you explain this answer? covers all topics & solutions for Mechanical Engineering 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for The ratio of thermal conductivity to electrical conductivity is equal toa)Prandtl numberb)Schmidt numberc)Lorentz numberd)Lewis numberCorrect answer is option 'C'. Can you explain this answer?.
The ratio of thermal conductivity to electrical conductivity is equal toa)Prandtl numberb)Schmidt numberc)Lorentz numberd)Lewis numberCorrect answer is option 'C'. Can you explain this answer? for Mechanical Engineering 2025 is part of Mechanical Engineering preparation. The Question and answers have been prepared according to the Mechanical Engineering exam syllabus. Information about The ratio of thermal conductivity to electrical conductivity is equal toa)Prandtl numberb)Schmidt numberc)Lorentz numberd)Lewis numberCorrect answer is option 'C'. Can you explain this answer? covers all topics & solutions for Mechanical Engineering 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for The ratio of thermal conductivity to electrical conductivity is equal toa)Prandtl numberb)Schmidt numberc)Lorentz numberd)Lewis numberCorrect answer is option 'C'. Can you explain this answer?.
Solutions for The ratio of thermal conductivity to electrical conductivity is equal toa)Prandtl numberb)Schmidt numberc)Lorentz numberd)Lewis numberCorrect answer is option 'C'. Can you explain this answer? in English & in Hindi are available as part of our courses for Mechanical Engineering.
Download more important topics, notes, lectures and mock test series for Mechanical Engineering Exam by signing up for free.
Here you can find the meaning of The ratio of thermal conductivity to electrical conductivity is equal toa)Prandtl numberb)Schmidt numberc)Lorentz numberd)Lewis numberCorrect answer is option 'C'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
The ratio of thermal conductivity to electrical conductivity is equal toa)Prandtl numberb)Schmidt numberc)Lorentz numberd)Lewis numberCorrect answer is option 'C'. Can you explain this answer?, a detailed solution for The ratio of thermal conductivity to electrical conductivity is equal toa)Prandtl numberb)Schmidt numberc)Lorentz numberd)Lewis numberCorrect answer is option 'C'. Can you explain this answer? has been provided alongside types of The ratio of thermal conductivity to electrical conductivity is equal toa)Prandtl numberb)Schmidt numberc)Lorentz numberd)Lewis numberCorrect answer is option 'C'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice The ratio of thermal conductivity to electrical conductivity is equal toa)Prandtl numberb)Schmidt numberc)Lorentz numberd)Lewis numberCorrect answer is option 'C'. Can you explain this answer? tests, examples and also practice Mechanical Engineering tests.

|
Explore Courses for Mechanical Engineering exam
|

|
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.























