Computer Science Engineering (CSE) Exam > Computer Science Engineering (CSE) Questions > A club has 256 members of whom 144 can play f...
Start Learning for Free
A club has 256 members of whom 144 can play football, 123 can play tennis, and 132 can play cricket. Moreover, 58 members can play both football and tennis, 25 can play both cricket and tennis, while 63 can play both football and cricket. If every member can play at least one game, then the number of members who can play only tennis is
- a)32
- b)43
- c)38
- d)45
Correct answer is option 'B'. Can you explain this answer?
| FREE This question is part of | Download PDF Attempt this Test |
Verified Answer
A club has 256 members of whom 144 can play football, 123 can play ten...
From observing the data given, we find that it is a closed 3 set Venn diagram.
Let the three sports be F, T and C for Football, Tennis and Cricket respectively
n (F U T U C) = 256 , n(F) = 144, n(T) = 123, n(C) = 132, n(F ∩ T) = 58, n(C ∩T) = 25, n(F ∩ C) = 63
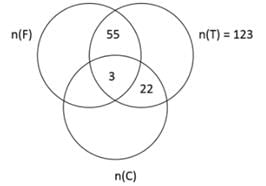
We know that (A U B U C) = n(A) + n(B) +n(C) - n(A ∩ B) - n(B ∩ C) - n(C ∩ A) + n(A ∩B ∩ C)
So, 256 = 144 + 123 + 132 - 58 - 25 - 63 + n (F ∩ T ∩ C)
n (F ∩ T ∩ C) = 256 - 144 + 123 +132 - 146
n (F ∩ T ∩ C) = 256 - 253 = 3
Now, it is easy to calculate the number of students who only play tennis using a Venn diagram.
n (Students who play only Tennis) = 123 - (55 + 3 + 22) = 123 - 80
n (Students who play only Tennis) = 43 students
n (F U T U C) = 256 , n(F) = 144, n(T) = 123, n(C) = 132, n(F ∩ T) = 58, n(C ∩T) = 25, n(F ∩ C) = 63

We know that (A U B U C) = n(A) + n(B) +n(C) - n(A ∩ B) - n(B ∩ C) - n(C ∩ A) + n(A ∩B ∩ C)
So, 256 = 144 + 123 + 132 - 58 - 25 - 63 + n (F ∩ T ∩ C)
n (F ∩ T ∩ C) = 256 - 144 + 123 +132 - 146
n (F ∩ T ∩ C) = 256 - 253 = 3
Now, it is easy to calculate the number of students who only play tennis using a Venn diagram.
n (Students who play only Tennis) = 123 - (55 + 3 + 22) = 123 - 80
n (Students who play only Tennis) = 43 students
Most Upvoted Answer
A club has 256 members of whom 144 can play football, 123 can play ten...
To solve this problem, we can use the principle of inclusion-exclusion. Let's break down the information given in the question:
- Total number of members in the club: 256
- Number of members who can play football: 144
- Number of members who can play tennis: 123
- Number of members who can play cricket: 132
- Number of members who can play both football and tennis: 58
- Number of members who can play both cricket and tennis: 25
- Number of members who can play both football and cricket: 63
We need to find the number of members who can play only tennis.
Step 1: Find the total number of members who can play tennis
- We know that 123 members can play tennis.
- However, this count includes members who can play both football and tennis as well as members who can play both cricket and tennis.
- So, we need to subtract the count of these overlapping members.
Step 2: Find the count of members who can play both football and tennis
- We know that 58 members can play both football and tennis.
Step 3: Find the count of members who can play both cricket and tennis
- We know that 25 members can play both cricket and tennis.
Step 4: Find the count of members who can play all three sports (football, tennis, and cricket)
- We know that 63 members can play all three sports.
Step 5: Calculate the count of members who can play only tennis
- To do this, we subtract the count of overlapping members (step 2 + step 3 + step 4) from the total count of tennis players (step 1).
- 123 - (58 + 25 + 63) = 123 - 146 = -23
Step 6: Adjust for the principle of inclusion-exclusion
- The negative count in step 5 indicates that there is an error in the calculations.
- This is likely due to some members being counted multiple times.
- To adjust for this, we need to add back the count of members who can play both football and cricket.
Step 7: Find the count of members who can play both football and cricket
- We know that 63 members can play both football and cricket.
Step 8: Recalculate the count of members who can play only tennis
- We add the count of members who can play both football and cricket (step 7) to the previous result (step 5).
- -23 + 63 = 40
Step 9: Adjust for the principle of inclusion-exclusion again
- The positive count in step 8 indicates that there is still an error in the calculations.
- This is likely due to some members being counted multiple times.
- To adjust for this, we need to subtract the count of members who can play all three sports (football, tennis, and cricket).
Step 10: Find the count of members who can play all three sports
- We know that 63 members can play all three sports.
Step 11: Recalculate the count of members who can play only tennis
- We subtract the count of members who can play all three sports (step 10) from the previous result (step 8).
- 40 - 63 = -23
Step 12: Final adjustment for the principle of inclusion-exclusion
- The negative count in step
- Total number of members in the club: 256
- Number of members who can play football: 144
- Number of members who can play tennis: 123
- Number of members who can play cricket: 132
- Number of members who can play both football and tennis: 58
- Number of members who can play both cricket and tennis: 25
- Number of members who can play both football and cricket: 63
We need to find the number of members who can play only tennis.
Step 1: Find the total number of members who can play tennis
- We know that 123 members can play tennis.
- However, this count includes members who can play both football and tennis as well as members who can play both cricket and tennis.
- So, we need to subtract the count of these overlapping members.
Step 2: Find the count of members who can play both football and tennis
- We know that 58 members can play both football and tennis.
Step 3: Find the count of members who can play both cricket and tennis
- We know that 25 members can play both cricket and tennis.
Step 4: Find the count of members who can play all three sports (football, tennis, and cricket)
- We know that 63 members can play all three sports.
Step 5: Calculate the count of members who can play only tennis
- To do this, we subtract the count of overlapping members (step 2 + step 3 + step 4) from the total count of tennis players (step 1).
- 123 - (58 + 25 + 63) = 123 - 146 = -23
Step 6: Adjust for the principle of inclusion-exclusion
- The negative count in step 5 indicates that there is an error in the calculations.
- This is likely due to some members being counted multiple times.
- To adjust for this, we need to add back the count of members who can play both football and cricket.
Step 7: Find the count of members who can play both football and cricket
- We know that 63 members can play both football and cricket.
Step 8: Recalculate the count of members who can play only tennis
- We add the count of members who can play both football and cricket (step 7) to the previous result (step 5).
- -23 + 63 = 40
Step 9: Adjust for the principle of inclusion-exclusion again
- The positive count in step 8 indicates that there is still an error in the calculations.
- This is likely due to some members being counted multiple times.
- To adjust for this, we need to subtract the count of members who can play all three sports (football, tennis, and cricket).
Step 10: Find the count of members who can play all three sports
- We know that 63 members can play all three sports.
Step 11: Recalculate the count of members who can play only tennis
- We subtract the count of members who can play all three sports (step 10) from the previous result (step 8).
- 40 - 63 = -23
Step 12: Final adjustment for the principle of inclusion-exclusion
- The negative count in step
Attention Computer Science Engineering (CSE) Students!
To make sure you are not studying endlessly, EduRev has designed Computer Science Engineering (CSE) study material, with Structured Courses, Videos, & Test Series. Plus get personalized analysis, doubt solving and improvement plans to achieve a great score in Computer Science Engineering (CSE).

|
Explore Courses for Computer Science Engineering (CSE) exam
|

|
Similar Computer Science Engineering (CSE) Doubts
A club has 256 members of whom 144 can play football, 123 can play tennis, and 132 can play cricket. Moreover, 58 members can play both football and tennis, 25 can play both cricket and tennis, while 63 can play both football and cricket. If every member can play at least one game, then the number of members who can play only tennis isa)32b)43c)38d)45Correct answer is option 'B'. Can you explain this answer?
Question Description
A club has 256 members of whom 144 can play football, 123 can play tennis, and 132 can play cricket. Moreover, 58 members can play both football and tennis, 25 can play both cricket and tennis, while 63 can play both football and cricket. If every member can play at least one game, then the number of members who can play only tennis isa)32b)43c)38d)45Correct answer is option 'B'. Can you explain this answer? for Computer Science Engineering (CSE) 2024 is part of Computer Science Engineering (CSE) preparation. The Question and answers have been prepared according to the Computer Science Engineering (CSE) exam syllabus. Information about A club has 256 members of whom 144 can play football, 123 can play tennis, and 132 can play cricket. Moreover, 58 members can play both football and tennis, 25 can play both cricket and tennis, while 63 can play both football and cricket. If every member can play at least one game, then the number of members who can play only tennis isa)32b)43c)38d)45Correct answer is option 'B'. Can you explain this answer? covers all topics & solutions for Computer Science Engineering (CSE) 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for A club has 256 members of whom 144 can play football, 123 can play tennis, and 132 can play cricket. Moreover, 58 members can play both football and tennis, 25 can play both cricket and tennis, while 63 can play both football and cricket. If every member can play at least one game, then the number of members who can play only tennis isa)32b)43c)38d)45Correct answer is option 'B'. Can you explain this answer?.
A club has 256 members of whom 144 can play football, 123 can play tennis, and 132 can play cricket. Moreover, 58 members can play both football and tennis, 25 can play both cricket and tennis, while 63 can play both football and cricket. If every member can play at least one game, then the number of members who can play only tennis isa)32b)43c)38d)45Correct answer is option 'B'. Can you explain this answer? for Computer Science Engineering (CSE) 2024 is part of Computer Science Engineering (CSE) preparation. The Question and answers have been prepared according to the Computer Science Engineering (CSE) exam syllabus. Information about A club has 256 members of whom 144 can play football, 123 can play tennis, and 132 can play cricket. Moreover, 58 members can play both football and tennis, 25 can play both cricket and tennis, while 63 can play both football and cricket. If every member can play at least one game, then the number of members who can play only tennis isa)32b)43c)38d)45Correct answer is option 'B'. Can you explain this answer? covers all topics & solutions for Computer Science Engineering (CSE) 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for A club has 256 members of whom 144 can play football, 123 can play tennis, and 132 can play cricket. Moreover, 58 members can play both football and tennis, 25 can play both cricket and tennis, while 63 can play both football and cricket. If every member can play at least one game, then the number of members who can play only tennis isa)32b)43c)38d)45Correct answer is option 'B'. Can you explain this answer?.
Solutions for A club has 256 members of whom 144 can play football, 123 can play tennis, and 132 can play cricket. Moreover, 58 members can play both football and tennis, 25 can play both cricket and tennis, while 63 can play both football and cricket. If every member can play at least one game, then the number of members who can play only tennis isa)32b)43c)38d)45Correct answer is option 'B'. Can you explain this answer? in English & in Hindi are available as part of our courses for Computer Science Engineering (CSE).
Download more important topics, notes, lectures and mock test series for Computer Science Engineering (CSE) Exam by signing up for free.
Here you can find the meaning of A club has 256 members of whom 144 can play football, 123 can play tennis, and 132 can play cricket. Moreover, 58 members can play both football and tennis, 25 can play both cricket and tennis, while 63 can play both football and cricket. If every member can play at least one game, then the number of members who can play only tennis isa)32b)43c)38d)45Correct answer is option 'B'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
A club has 256 members of whom 144 can play football, 123 can play tennis, and 132 can play cricket. Moreover, 58 members can play both football and tennis, 25 can play both cricket and tennis, while 63 can play both football and cricket. If every member can play at least one game, then the number of members who can play only tennis isa)32b)43c)38d)45Correct answer is option 'B'. Can you explain this answer?, a detailed solution for A club has 256 members of whom 144 can play football, 123 can play tennis, and 132 can play cricket. Moreover, 58 members can play both football and tennis, 25 can play both cricket and tennis, while 63 can play both football and cricket. If every member can play at least one game, then the number of members who can play only tennis isa)32b)43c)38d)45Correct answer is option 'B'. Can you explain this answer? has been provided alongside types of A club has 256 members of whom 144 can play football, 123 can play tennis, and 132 can play cricket. Moreover, 58 members can play both football and tennis, 25 can play both cricket and tennis, while 63 can play both football and cricket. If every member can play at least one game, then the number of members who can play only tennis isa)32b)43c)38d)45Correct answer is option 'B'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice A club has 256 members of whom 144 can play football, 123 can play tennis, and 132 can play cricket. Moreover, 58 members can play both football and tennis, 25 can play both cricket and tennis, while 63 can play both football and cricket. If every member can play at least one game, then the number of members who can play only tennis isa)32b)43c)38d)45Correct answer is option 'B'. Can you explain this answer? tests, examples and also practice Computer Science Engineering (CSE) tests.

|
Explore Courses for Computer Science Engineering (CSE) exam
|

|
Suggested Free Tests
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.
























