Class 9 Exam > Class 9 Questions > 2. An iron sphere of 1kg is moving a velocity...
Start Learning for Free
2. An iron sphere of 1kg is moving a velocity of 20 m/s on a cemented floor. It comes to rest after traveling a distance of 50 m. Find the force of friction between the sphere and the floor. of Iriction?
Verified Answer
2. An iron sphere of 1kg is moving a velocity of 20 m/s on a cemented ...
Mass of sphere, m = 1kg
Initial velocity, u = 20 m/s
Final velocity, v = 0
Distance travelled, s = 50m
Let the friction acting = f
Here, the kinetic energy of the ball is being dissipated to overcome friction. So, according to conservation of energy,
The change in kinetic energy = work done by friction
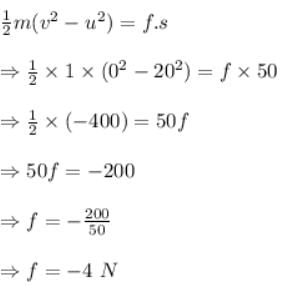
So friction acting is 4N. The negative sign denotes that it acts in the direction opposite to the motion of the sphere.
 This question is part of UPSC exam. View all Class 9 courses
This question is part of UPSC exam. View all Class 9 courses
Most Upvoted Answer
2. An iron sphere of 1kg is moving a velocity of 20 m/s on a cemented ...
Force of Friction between the Sphere and the Floor
Given:
Mass of the iron sphere (m) = 1 kg
Initial velocity of the sphere (u) = 20 m/s
Distance traveled by the sphere (s) = 50 m
To find:
Force of friction between the sphere and the floor (Ff)
Using the kinematic equation:
v^2 = u^2 + 2as
where v is the final velocity and a is the acceleration.
First, let's find the final velocity (v) of the sphere when it comes to rest. Since it comes to rest, the final velocity is 0 m/s.
0 = (20 m/s)^2 + 2a(50 m)
0 = 400 m^2/s^2 + 100a m
a = -400/100 = -4 m/s^2
The negative sign indicates that the acceleration is in the opposite direction to the initial velocity, which is due to the force of friction acting against the motion of the sphere.
Using Newton's second law of motion:
F = ma
where F is the force, m is the mass, and a is the acceleration.
The force of friction (Ff) is given by:
Ff = μN
where μ is the coefficient of friction and N is the normal force.
Since the sphere is on a horizontal surface, the normal force is equal to the weight of the sphere (N = mg).
Let's assume the coefficient of friction between the iron sphere and the cemented floor is μ.
Ff = μN
Ff = μmg
Now, substituting the values:
Ff = μ(1 kg)(9.8 m/s^2)
Ff = 9.8μ N
So, the force of friction between the iron sphere and the floor is 9.8μ Newtons.
Explanation:
- The force of friction between the sphere and the floor causes the sphere to slow down and eventually come to rest.
- The force of friction is directly proportional to the normal force and the coefficient of friction.
- The normal force is the force exerted by the floor on the sphere in the vertical direction and is equal to the weight of the sphere.
- The coefficient of friction represents the roughness or smoothness of the surfaces in contact.
- The negative acceleration indicates that the sphere is decelerating or slowing down.
- The force of friction always acts in the opposite direction to the motion of the object.
- In this case, the force of friction opposes the motion of the sphere, causing it to slow down and eventually come to rest.
Given:
Mass of the iron sphere (m) = 1 kg
Initial velocity of the sphere (u) = 20 m/s
Distance traveled by the sphere (s) = 50 m
To find:
Force of friction between the sphere and the floor (Ff)
Using the kinematic equation:
v^2 = u^2 + 2as
where v is the final velocity and a is the acceleration.
First, let's find the final velocity (v) of the sphere when it comes to rest. Since it comes to rest, the final velocity is 0 m/s.
0 = (20 m/s)^2 + 2a(50 m)
0 = 400 m^2/s^2 + 100a m
a = -400/100 = -4 m/s^2
The negative sign indicates that the acceleration is in the opposite direction to the initial velocity, which is due to the force of friction acting against the motion of the sphere.
Using Newton's second law of motion:
F = ma
where F is the force, m is the mass, and a is the acceleration.
The force of friction (Ff) is given by:
Ff = μN
where μ is the coefficient of friction and N is the normal force.
Since the sphere is on a horizontal surface, the normal force is equal to the weight of the sphere (N = mg).
Let's assume the coefficient of friction between the iron sphere and the cemented floor is μ.
Ff = μN
Ff = μmg
Now, substituting the values:
Ff = μ(1 kg)(9.8 m/s^2)
Ff = 9.8μ N
So, the force of friction between the iron sphere and the floor is 9.8μ Newtons.
Explanation:
- The force of friction between the sphere and the floor causes the sphere to slow down and eventually come to rest.
- The force of friction is directly proportional to the normal force and the coefficient of friction.
- The normal force is the force exerted by the floor on the sphere in the vertical direction and is equal to the weight of the sphere.
- The coefficient of friction represents the roughness or smoothness of the surfaces in contact.
- The negative acceleration indicates that the sphere is decelerating or slowing down.
- The force of friction always acts in the opposite direction to the motion of the object.
- In this case, the force of friction opposes the motion of the sphere, causing it to slow down and eventually come to rest.
Attention Class 9 Students!
To make sure you are not studying endlessly, EduRev has designed Class 9 study material, with Structured Courses, Videos, & Test Series. Plus get personalized analysis, doubt solving and improvement plans to achieve a great score in Class 9.

|
Explore Courses for Class 9 exam
|

|
Similar Class 9 Doubts
2. An iron sphere of 1kg is moving a velocity of 20 m/s on a cemented floor. It comes to rest after traveling a distance of 50 m. Find the force of friction between the sphere and the floor. of Iriction?
Question Description
2. An iron sphere of 1kg is moving a velocity of 20 m/s on a cemented floor. It comes to rest after traveling a distance of 50 m. Find the force of friction between the sphere and the floor. of Iriction? for Class 9 2024 is part of Class 9 preparation. The Question and answers have been prepared according to the Class 9 exam syllabus. Information about 2. An iron sphere of 1kg is moving a velocity of 20 m/s on a cemented floor. It comes to rest after traveling a distance of 50 m. Find the force of friction between the sphere and the floor. of Iriction? covers all topics & solutions for Class 9 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for 2. An iron sphere of 1kg is moving a velocity of 20 m/s on a cemented floor. It comes to rest after traveling a distance of 50 m. Find the force of friction between the sphere and the floor. of Iriction?.
2. An iron sphere of 1kg is moving a velocity of 20 m/s on a cemented floor. It comes to rest after traveling a distance of 50 m. Find the force of friction between the sphere and the floor. of Iriction? for Class 9 2024 is part of Class 9 preparation. The Question and answers have been prepared according to the Class 9 exam syllabus. Information about 2. An iron sphere of 1kg is moving a velocity of 20 m/s on a cemented floor. It comes to rest after traveling a distance of 50 m. Find the force of friction between the sphere and the floor. of Iriction? covers all topics & solutions for Class 9 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for 2. An iron sphere of 1kg is moving a velocity of 20 m/s on a cemented floor. It comes to rest after traveling a distance of 50 m. Find the force of friction between the sphere and the floor. of Iriction?.
Solutions for 2. An iron sphere of 1kg is moving a velocity of 20 m/s on a cemented floor. It comes to rest after traveling a distance of 50 m. Find the force of friction between the sphere and the floor. of Iriction? in English & in Hindi are available as part of our courses for Class 9.
Download more important topics, notes, lectures and mock test series for Class 9 Exam by signing up for free.
Here you can find the meaning of 2. An iron sphere of 1kg is moving a velocity of 20 m/s on a cemented floor. It comes to rest after traveling a distance of 50 m. Find the force of friction between the sphere and the floor. of Iriction? defined & explained in the simplest way possible. Besides giving the explanation of
2. An iron sphere of 1kg is moving a velocity of 20 m/s on a cemented floor. It comes to rest after traveling a distance of 50 m. Find the force of friction between the sphere and the floor. of Iriction?, a detailed solution for 2. An iron sphere of 1kg is moving a velocity of 20 m/s on a cemented floor. It comes to rest after traveling a distance of 50 m. Find the force of friction between the sphere and the floor. of Iriction? has been provided alongside types of 2. An iron sphere of 1kg is moving a velocity of 20 m/s on a cemented floor. It comes to rest after traveling a distance of 50 m. Find the force of friction between the sphere and the floor. of Iriction? theory, EduRev gives you an
ample number of questions to practice 2. An iron sphere of 1kg is moving a velocity of 20 m/s on a cemented floor. It comes to rest after traveling a distance of 50 m. Find the force of friction between the sphere and the floor. of Iriction? tests, examples and also practice Class 9 tests.

|
Explore Courses for Class 9 exam
|

|
Suggested Free Tests
Test: The Fundamental Unit of Life- Case Based Type Questions- 1
Test | 10 questions
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.

























