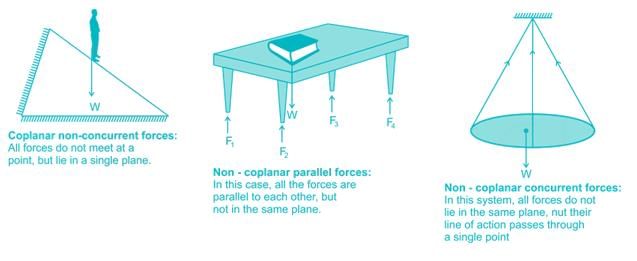
Non-Coplanar Concurrent Forces

Non-coplanar concurrent forces refer to forces that meet at a single point but have their lines of action in different planes. In this scenario, the forces do not lie in the same plane or have the same direction, but they do intersect at a common point.

Explanation:

When forces act on an object, they have a point of application and a direction. The point of application is the location where the force is applied to the object, and the direction indicates the line along which the force acts. When multiple forces act on an object, it is important to consider their points of application and directions in order to determine the resultant effect on the object.

In the case of coplanar forces, all the forces lie in the same plane. This means that their lines of action can be represented by a two-dimensional diagram. Coplanar forces can be concurrent or non-concurrent. Concurrent forces meet at a single point, known as the point of concurrency. Their lines of action can be represented by lines passing through this point.

Non-coplanar forces, on the other hand, do not lie in the same plane. They have lines of action that extend into three-dimensional space. Non-coplanar forces can also be concurrent or non-concurrent. When forces are non-coplanar and concurrent, it means that they meet at a single point, but their lines of action do not lie in the same plane. This can be visualized as lines passing through a common point, but the lines are not confined to a single plane.

Example:

Imagine a three-dimensional object, such as a pyramid, with forces acting on different sides. Each force has a point of application and a direction. If these forces meet at a single point within the pyramid, but their lines of action extend into different planes, they are considered non-coplanar concurrent forces.

In such a scenario, it becomes important to analyze the magnitudes and directions of these forces to determine their resultant effect on the object. The principles of vector addition and resolution can be applied to compute the net force and its direction.

Overall, non-coplanar concurrent forces are forces that intersect at a single point but have their lines of action in different planes. They are an important concept in the study of mechanics and are often encountered in real-world situations involving three-dimensional objects and complex force systems.