Defence Exam > Defence Questions > The mass flow through a convergent – di...
Start Learning for Free
The mass flow through a convergent – divergent nozzle is maximum when the pressure at:
- a)Exit is equal to the critical pressure
- b)Exit is less than atmospheric pressure
- c)Throat is equal to the exit pressure
- d)Throat is equal to the critical pressure
Correct answer is option 'D'. Can you explain this answer?
| FREE This question is part of | Download PDF Attempt this Test |
Verified Answer
The mass flow through a convergent – divergent nozzle is maximum...
Choked flow is a limiting condition where the mass flow will not increase with a further decrease in the downstream pressure environment while upstream pressure is fixed.
For chocked flow in convergent – divergent nozzle, Mach number at throat is equal to 1 and the pressure at throat is equal to the critical pressure.
Critical pressure ratio for a choked nozzle:
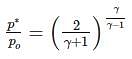
Where p* is the critical pressure and p0 is the inlet pressure
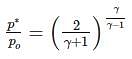
Where p* is the critical pressure and p0 is the inlet pressure
Most Upvoted Answer
The mass flow through a convergent – divergent nozzle is maximum...
The mass flow through a convergent nozzle can be calculated using the continuity equation, which states that the mass flow rate is constant for an incompressible fluid.
The continuity equation is given by:
A1 * V1 = A2 * V2
where A1 and A2 are the cross-sectional areas of the nozzle at the inlet and outlet, respectively, and V1 and V2 are the velocities of the fluid at the inlet and outlet, respectively.
In a convergent nozzle, the area decreases as the fluid flows from the inlet to the outlet, and therefore the velocity increases. This means that A1 > A2 and V1 < v2.="" />
To calculate the mass flow rate, we can rearrange the equation to solve for the velocity at the outlet:
V2 = (A1/A2) * V1
The mass flow rate (m_dot) is then given by:
m_dot = rho * A2 * V2
where rho is the density of the fluid.
Substituting the expression for V2, we get:
m_dot = rho * A2 * ((A1/A2) * V1)
Simplifying, we get:
m_dot = rho * A1 * V1
So, the mass flow rate through a convergent nozzle can be calculated by multiplying the density of the fluid by the cross-sectional area of the nozzle at the inlet (A1) and the velocity of the fluid at the inlet (V1).
The continuity equation is given by:
A1 * V1 = A2 * V2
where A1 and A2 are the cross-sectional areas of the nozzle at the inlet and outlet, respectively, and V1 and V2 are the velocities of the fluid at the inlet and outlet, respectively.
In a convergent nozzle, the area decreases as the fluid flows from the inlet to the outlet, and therefore the velocity increases. This means that A1 > A2 and V1 < v2.="" />
To calculate the mass flow rate, we can rearrange the equation to solve for the velocity at the outlet:
V2 = (A1/A2) * V1
The mass flow rate (m_dot) is then given by:
m_dot = rho * A2 * V2
where rho is the density of the fluid.
Substituting the expression for V2, we get:
m_dot = rho * A2 * ((A1/A2) * V1)
Simplifying, we get:
m_dot = rho * A1 * V1
So, the mass flow rate through a convergent nozzle can be calculated by multiplying the density of the fluid by the cross-sectional area of the nozzle at the inlet (A1) and the velocity of the fluid at the inlet (V1).

|
Explore Courses for Defence exam
|

|
Similar Defence Doubts
The mass flow through a convergent – divergent nozzle is maximum when the pressure at:a)Exit is equal to the critical pressureb)Exit is less than atmospheric pressurec)Throat is equal to the exit pressured)Throat is equal to the critical pressureCorrect answer is option 'D'. Can you explain this answer?
Question Description
The mass flow through a convergent – divergent nozzle is maximum when the pressure at:a)Exit is equal to the critical pressureb)Exit is less than atmospheric pressurec)Throat is equal to the exit pressured)Throat is equal to the critical pressureCorrect answer is option 'D'. Can you explain this answer? for Defence 2024 is part of Defence preparation. The Question and answers have been prepared according to the Defence exam syllabus. Information about The mass flow through a convergent – divergent nozzle is maximum when the pressure at:a)Exit is equal to the critical pressureb)Exit is less than atmospheric pressurec)Throat is equal to the exit pressured)Throat is equal to the critical pressureCorrect answer is option 'D'. Can you explain this answer? covers all topics & solutions for Defence 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for The mass flow through a convergent – divergent nozzle is maximum when the pressure at:a)Exit is equal to the critical pressureb)Exit is less than atmospheric pressurec)Throat is equal to the exit pressured)Throat is equal to the critical pressureCorrect answer is option 'D'. Can you explain this answer?.
The mass flow through a convergent – divergent nozzle is maximum when the pressure at:a)Exit is equal to the critical pressureb)Exit is less than atmospheric pressurec)Throat is equal to the exit pressured)Throat is equal to the critical pressureCorrect answer is option 'D'. Can you explain this answer? for Defence 2024 is part of Defence preparation. The Question and answers have been prepared according to the Defence exam syllabus. Information about The mass flow through a convergent – divergent nozzle is maximum when the pressure at:a)Exit is equal to the critical pressureb)Exit is less than atmospheric pressurec)Throat is equal to the exit pressured)Throat is equal to the critical pressureCorrect answer is option 'D'. Can you explain this answer? covers all topics & solutions for Defence 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for The mass flow through a convergent – divergent nozzle is maximum when the pressure at:a)Exit is equal to the critical pressureb)Exit is less than atmospheric pressurec)Throat is equal to the exit pressured)Throat is equal to the critical pressureCorrect answer is option 'D'. Can you explain this answer?.
Solutions for The mass flow through a convergent – divergent nozzle is maximum when the pressure at:a)Exit is equal to the critical pressureb)Exit is less than atmospheric pressurec)Throat is equal to the exit pressured)Throat is equal to the critical pressureCorrect answer is option 'D'. Can you explain this answer? in English & in Hindi are available as part of our courses for Defence.
Download more important topics, notes, lectures and mock test series for Defence Exam by signing up for free.
Here you can find the meaning of The mass flow through a convergent – divergent nozzle is maximum when the pressure at:a)Exit is equal to the critical pressureb)Exit is less than atmospheric pressurec)Throat is equal to the exit pressured)Throat is equal to the critical pressureCorrect answer is option 'D'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
The mass flow through a convergent – divergent nozzle is maximum when the pressure at:a)Exit is equal to the critical pressureb)Exit is less than atmospheric pressurec)Throat is equal to the exit pressured)Throat is equal to the critical pressureCorrect answer is option 'D'. Can you explain this answer?, a detailed solution for The mass flow through a convergent – divergent nozzle is maximum when the pressure at:a)Exit is equal to the critical pressureb)Exit is less than atmospheric pressurec)Throat is equal to the exit pressured)Throat is equal to the critical pressureCorrect answer is option 'D'. Can you explain this answer? has been provided alongside types of The mass flow through a convergent – divergent nozzle is maximum when the pressure at:a)Exit is equal to the critical pressureb)Exit is less than atmospheric pressurec)Throat is equal to the exit pressured)Throat is equal to the critical pressureCorrect answer is option 'D'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice The mass flow through a convergent – divergent nozzle is maximum when the pressure at:a)Exit is equal to the critical pressureb)Exit is less than atmospheric pressurec)Throat is equal to the exit pressured)Throat is equal to the critical pressureCorrect answer is option 'D'. Can you explain this answer? tests, examples and also practice Defence tests.

|
Explore Courses for Defence exam
|

|
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.


















