Defence Exam > Defence Questions > In solving a lumped parameter problem, which ...
Start Learning for Free
In solving a lumped parameter problem, which one of the following pair of non-dimensional numbers is used?
- a)Grashoff number and Biot number
- b)Prandtl number and Nusselt number
- c)Biot number and Fourier number
- d)Fourier number and Reynolds number
Correct answer is option 'C'. Can you explain this answer?
| FREE This question is part of | Download PDF Attempt this Test |
Verified Answer
In solving a lumped parameter problem, which one of the following pair...
Biot number is the ratio of internal conduction resistance within solid to external convective resistance at body surface.
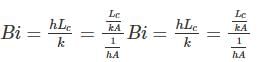
Small Biot number shows conduction resistance is less important. In this case we use Lumped capacitance analysis. According to which:
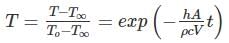
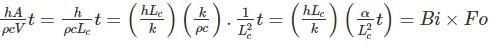
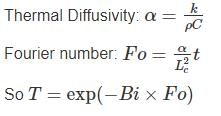
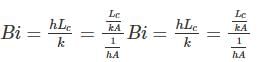
Small Biot number shows conduction resistance is less important. In this case we use Lumped capacitance analysis. According to which:
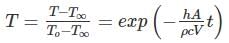
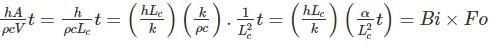
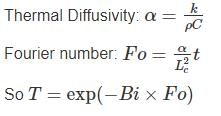
Most Upvoted Answer
In solving a lumped parameter problem, which one of the following pair...
Non-dimensional numbers are used in engineering and physics to analyze and compare different systems without the need to consider their specific dimensions. They provide valuable information about the behavior and characteristics of the system being studied.
In the context of solving a lumped parameter problem, which involves analyzing the behavior of a system as a whole rather than considering individual regions or components, the pair of non-dimensional numbers used is the Biot number and the Fourier number. Let's understand the significance of each of these numbers:
1. Biot number (Bi):
The Biot number is a dimensionless number that relates the heat transfer resistance inside a solid to the heat transfer resistance at the surface of the solid. It is defined as the ratio of the internal thermal resistance to the external thermal resistance. Mathematically, it can be expressed as:
Bi = hL / k
where h is the convective heat transfer coefficient, L is a characteristic length, and k is the thermal conductivity of the material.
The Biot number helps determine whether the heat transfer within the solid is primarily controlled by conduction or convection. A large Biot number indicates that convection dominates, while a small Biot number indicates that conduction dominates.
2. Fourier number (Fo):
The Fourier number is a dimensionless number that characterizes the transient heat conduction behavior in a solid. It represents the ratio of the time taken for heat conduction to occur over a characteristic time scale. Mathematically, it can be expressed as:
Fo = αt / L^2
where α is the thermal diffusivity of the material, t is time, and L is a characteristic length.
The Fourier number helps determine the rate at which heat is transferred within the solid. A large Fourier number indicates that heat conduction occurs rapidly, while a small Fourier number indicates that heat conduction occurs slowly.
The combination of the Biot number and the Fourier number is used in solving lumped parameter problems because they provide valuable information about the heat transfer behavior and the time required for heat conduction within the system. By analyzing these non-dimensional numbers, engineers and scientists can evaluate the transient behavior and design appropriate systems for efficient heat transfer.
In the context of solving a lumped parameter problem, which involves analyzing the behavior of a system as a whole rather than considering individual regions or components, the pair of non-dimensional numbers used is the Biot number and the Fourier number. Let's understand the significance of each of these numbers:
1. Biot number (Bi):
The Biot number is a dimensionless number that relates the heat transfer resistance inside a solid to the heat transfer resistance at the surface of the solid. It is defined as the ratio of the internal thermal resistance to the external thermal resistance. Mathematically, it can be expressed as:
Bi = hL / k
where h is the convective heat transfer coefficient, L is a characteristic length, and k is the thermal conductivity of the material.
The Biot number helps determine whether the heat transfer within the solid is primarily controlled by conduction or convection. A large Biot number indicates that convection dominates, while a small Biot number indicates that conduction dominates.
2. Fourier number (Fo):
The Fourier number is a dimensionless number that characterizes the transient heat conduction behavior in a solid. It represents the ratio of the time taken for heat conduction to occur over a characteristic time scale. Mathematically, it can be expressed as:
Fo = αt / L^2
where α is the thermal diffusivity of the material, t is time, and L is a characteristic length.
The Fourier number helps determine the rate at which heat is transferred within the solid. A large Fourier number indicates that heat conduction occurs rapidly, while a small Fourier number indicates that heat conduction occurs slowly.
The combination of the Biot number and the Fourier number is used in solving lumped parameter problems because they provide valuable information about the heat transfer behavior and the time required for heat conduction within the system. By analyzing these non-dimensional numbers, engineers and scientists can evaluate the transient behavior and design appropriate systems for efficient heat transfer.

|
Explore Courses for Defence exam
|

|
In solving a lumped parameter problem, which one of the following pair of non-dimensional numbers is used?a)Grashoff number and Biot numberb)Prandtl number and Nusselt numberc)Biot number and Fourier numberd)Fourier number and Reynolds numberCorrect answer is option 'C'. Can you explain this answer?
Question Description
In solving a lumped parameter problem, which one of the following pair of non-dimensional numbers is used?a)Grashoff number and Biot numberb)Prandtl number and Nusselt numberc)Biot number and Fourier numberd)Fourier number and Reynolds numberCorrect answer is option 'C'. Can you explain this answer? for Defence 2024 is part of Defence preparation. The Question and answers have been prepared according to the Defence exam syllabus. Information about In solving a lumped parameter problem, which one of the following pair of non-dimensional numbers is used?a)Grashoff number and Biot numberb)Prandtl number and Nusselt numberc)Biot number and Fourier numberd)Fourier number and Reynolds numberCorrect answer is option 'C'. Can you explain this answer? covers all topics & solutions for Defence 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for In solving a lumped parameter problem, which one of the following pair of non-dimensional numbers is used?a)Grashoff number and Biot numberb)Prandtl number and Nusselt numberc)Biot number and Fourier numberd)Fourier number and Reynolds numberCorrect answer is option 'C'. Can you explain this answer?.
In solving a lumped parameter problem, which one of the following pair of non-dimensional numbers is used?a)Grashoff number and Biot numberb)Prandtl number and Nusselt numberc)Biot number and Fourier numberd)Fourier number and Reynolds numberCorrect answer is option 'C'. Can you explain this answer? for Defence 2024 is part of Defence preparation. The Question and answers have been prepared according to the Defence exam syllabus. Information about In solving a lumped parameter problem, which one of the following pair of non-dimensional numbers is used?a)Grashoff number and Biot numberb)Prandtl number and Nusselt numberc)Biot number and Fourier numberd)Fourier number and Reynolds numberCorrect answer is option 'C'. Can you explain this answer? covers all topics & solutions for Defence 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for In solving a lumped parameter problem, which one of the following pair of non-dimensional numbers is used?a)Grashoff number and Biot numberb)Prandtl number and Nusselt numberc)Biot number and Fourier numberd)Fourier number and Reynolds numberCorrect answer is option 'C'. Can you explain this answer?.
Solutions for In solving a lumped parameter problem, which one of the following pair of non-dimensional numbers is used?a)Grashoff number and Biot numberb)Prandtl number and Nusselt numberc)Biot number and Fourier numberd)Fourier number and Reynolds numberCorrect answer is option 'C'. Can you explain this answer? in English & in Hindi are available as part of our courses for Defence.
Download more important topics, notes, lectures and mock test series for Defence Exam by signing up for free.
Here you can find the meaning of In solving a lumped parameter problem, which one of the following pair of non-dimensional numbers is used?a)Grashoff number and Biot numberb)Prandtl number and Nusselt numberc)Biot number and Fourier numberd)Fourier number and Reynolds numberCorrect answer is option 'C'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
In solving a lumped parameter problem, which one of the following pair of non-dimensional numbers is used?a)Grashoff number and Biot numberb)Prandtl number and Nusselt numberc)Biot number and Fourier numberd)Fourier number and Reynolds numberCorrect answer is option 'C'. Can you explain this answer?, a detailed solution for In solving a lumped parameter problem, which one of the following pair of non-dimensional numbers is used?a)Grashoff number and Biot numberb)Prandtl number and Nusselt numberc)Biot number and Fourier numberd)Fourier number and Reynolds numberCorrect answer is option 'C'. Can you explain this answer? has been provided alongside types of In solving a lumped parameter problem, which one of the following pair of non-dimensional numbers is used?a)Grashoff number and Biot numberb)Prandtl number and Nusselt numberc)Biot number and Fourier numberd)Fourier number and Reynolds numberCorrect answer is option 'C'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice In solving a lumped parameter problem, which one of the following pair of non-dimensional numbers is used?a)Grashoff number and Biot numberb)Prandtl number and Nusselt numberc)Biot number and Fourier numberd)Fourier number and Reynolds numberCorrect answer is option 'C'. Can you explain this answer? tests, examples and also practice Defence tests.

|
Explore Courses for Defence exam
|

|
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.
















