Civil Engineering (CE) Exam > Civil Engineering (CE) Questions > A pipeline conveys 8.23 litre per second of ...
Start Learning for Free
A pipeline conveys 8.23 litre per second of water from an overhead tank to a building. The pipe is 2 km long and 0.15 m in diameter. It is desired to increase the discharge by 30% by installing another pipeline in parallel with this over half the length. Suggest a suitable diameter of the pipe to be installed. Is there any upper limit on discharge augmentation by this arrangement? (Take friction factor f = 0.03. )
- a)0.16 m and Qmax = 0.021 m3/s
- b)0.17 m and Qmax = 0.012 m3/s
- c)0.16 m and Qmax = 0.012 m3/s
- d)0.17 m and Qmax = 0.021 m3/s
Correct answer is option 'C'. Can you explain this answer?
Verified Answer
A pipeline conveys 8.23 litre per second of water from an overhead ta...
The height H of the overhead tank above the building can be determined from the conditions with a single pipe.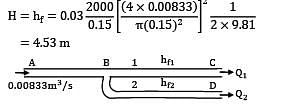
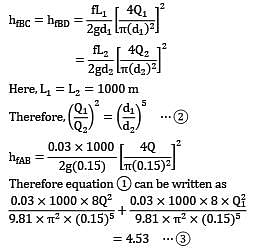
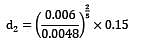
View all questions of this test
d = 0.15 m
l = 2 km
f = 0.03

In the new plan as shown in figure hf = 4.53 = hfAB + hfBC ⋯ ① again,
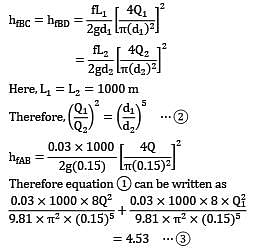
In this case, Q = 1.3 × 0.00833 = 0.0108 m3/s Then, from equation ③, we get
Q12 = 0.00014 − (0.0108)2
which gives Q1 = 0.0048 m3/s From continuity,
Q2 = 0.0108 − 0.0048
= 0.006 m3/s
From equation ②, we have
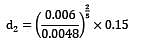
?2 = 0.1?? ?
It can be observed from equation ③ that
Q12 = 0.00014 − Q2
or Q2 = 0.00014 − Q21
Now, Q will be maximum when Q1 will be minimum. For a physically possible situation, the minimum value of Q1 will be zero. Therefore, the maximum value of Q will be
Qmax = √0.00014 = 0.0118 m3/s which is 41.6% more than the initial value. The case (Q1 = 0, Q = 0.0118 m3/s) corresponds to a situation of an infinitely large branched pipe, i.e. d2 → ∞.
Most Upvoted Answer
A pipeline conveys 8.23 litre per second of water from an overhead ta...
The height H of the overhead tank above the building can be determined from the conditions with a single pipe.
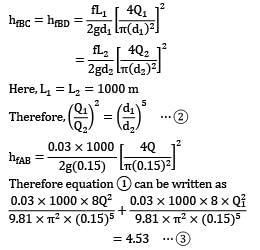

d = 0.15 m
l = 2 km
f = 0.03

In the new plan as shown in figure hf = 4.53 = hfAB + hfBC ⋯ ① again,
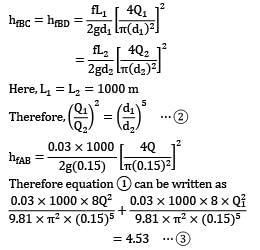
In this case, Q = 1.3 × 0.00833 = 0.0108 m3/s Then, from equation ③, we get
Q12 = 0.00014 − (0.0108)2
which gives Q1 = 0.0048 m3/s From continuity,
Q2 = 0.0108 − 0.0048
= 0.006 m3/s
From equation ②, we have

?2 = 0.1?? ?
It can be observed from equation ③ that
Q12 = 0.00014 − Q2
or Q2 = 0.00014 − Q21
Now, Q will be maximum when Q1 will be minimum. For a physically possible situation, the minimum value of Q1 will be zero. Therefore, the maximum value of Q will be
Qmax = √0.00014 = 0.0118 m3/s which is 41.6% more than the initial value. The case (Q1 = 0, Q = 0.0118 m3/s) corresponds to a situation of an infinitely large branched pipe, i.e. d2 → ∞.
Free Test
| FREE | Start Free Test |
Community Answer
A pipeline conveys 8.23 litre per second of water from an overhead ta...
The height H of the overhead tank above the building can be determined from the conditions with a single pipe.
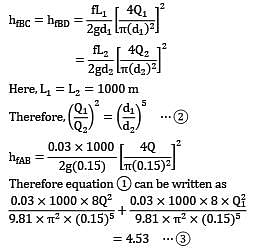
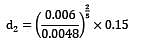
d = 0.15 m
l = 2 km
f = 0.03

In the new plan as shown in figure hf = 4.53 = hfAB + hfBC ⋯ ① again,
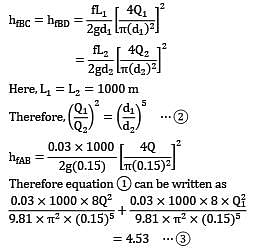
In this case, Q = 1.3 × 0.00833 = 0.0108 m3/s Then, from equation ③, we get
Q12 = 0.00014 − (0.0108)2
which gives Q1 = 0.0048 m3/s From continuity,
Q2 = 0.0108 − 0.0048
= 0.006 m3/s
From equation ②, we have
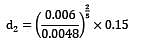
?2 = 0.1?? ?
It can be observed from equation ③ that
Q12 = 0.00014 − Q2
or Q2 = 0.00014 − Q21
Now, Q will be maximum when Q1 will be minimum. For a physically possible situation, the minimum value of Q1 will be zero. Therefore, the maximum value of Q will be
Qmax = √0.00014 = 0.0118 m3/s which is 41.6% more than the initial value. The case (Q1 = 0, Q = 0.0118 m3/s) corresponds to a situation of an infinitely large branched pipe, i.e. d2 → ∞.

|
Explore Courses for Civil Engineering (CE) exam
|

|
Similar Civil Engineering (CE) Doubts
A pipeline conveys 8.23 litre per second of water from an overhead tank to a building. The pipe is 2 km long and 0.15 m in diameter. It is desired to increase the discharge by 30% by installing another pipeline in parallel with this over half the length. Suggest a suitable diameter of the pipe to be installed. Is there any upper limit on discharge augmentation by this arrangement? (Take friction factor f = 0.03. )a) 0.16 m and Qmax = 0.021 m3/sb) 0.17 m and Qmax = 0.012 m3/sc) 0.16 m and Qmax = 0.012 m3/sd) 0.17 m and Qmax = 0.021 m3/sCorrect answer is option 'C'. Can you explain this answer?
Question Description
A pipeline conveys 8.23 litre per second of water from an overhead tank to a building. The pipe is 2 km long and 0.15 m in diameter. It is desired to increase the discharge by 30% by installing another pipeline in parallel with this over half the length. Suggest a suitable diameter of the pipe to be installed. Is there any upper limit on discharge augmentation by this arrangement? (Take friction factor f = 0.03. )a) 0.16 m and Qmax = 0.021 m3/sb) 0.17 m and Qmax = 0.012 m3/sc) 0.16 m and Qmax = 0.012 m3/sd) 0.17 m and Qmax = 0.021 m3/sCorrect answer is option 'C'. Can you explain this answer? for Civil Engineering (CE) 2025 is part of Civil Engineering (CE) preparation. The Question and answers have been prepared according to the Civil Engineering (CE) exam syllabus. Information about A pipeline conveys 8.23 litre per second of water from an overhead tank to a building. The pipe is 2 km long and 0.15 m in diameter. It is desired to increase the discharge by 30% by installing another pipeline in parallel with this over half the length. Suggest a suitable diameter of the pipe to be installed. Is there any upper limit on discharge augmentation by this arrangement? (Take friction factor f = 0.03. )a) 0.16 m and Qmax = 0.021 m3/sb) 0.17 m and Qmax = 0.012 m3/sc) 0.16 m and Qmax = 0.012 m3/sd) 0.17 m and Qmax = 0.021 m3/sCorrect answer is option 'C'. Can you explain this answer? covers all topics & solutions for Civil Engineering (CE) 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for A pipeline conveys 8.23 litre per second of water from an overhead tank to a building. The pipe is 2 km long and 0.15 m in diameter. It is desired to increase the discharge by 30% by installing another pipeline in parallel with this over half the length. Suggest a suitable diameter of the pipe to be installed. Is there any upper limit on discharge augmentation by this arrangement? (Take friction factor f = 0.03. )a) 0.16 m and Qmax = 0.021 m3/sb) 0.17 m and Qmax = 0.012 m3/sc) 0.16 m and Qmax = 0.012 m3/sd) 0.17 m and Qmax = 0.021 m3/sCorrect answer is option 'C'. Can you explain this answer?.
A pipeline conveys 8.23 litre per second of water from an overhead tank to a building. The pipe is 2 km long and 0.15 m in diameter. It is desired to increase the discharge by 30% by installing another pipeline in parallel with this over half the length. Suggest a suitable diameter of the pipe to be installed. Is there any upper limit on discharge augmentation by this arrangement? (Take friction factor f = 0.03. )a) 0.16 m and Qmax = 0.021 m3/sb) 0.17 m and Qmax = 0.012 m3/sc) 0.16 m and Qmax = 0.012 m3/sd) 0.17 m and Qmax = 0.021 m3/sCorrect answer is option 'C'. Can you explain this answer? for Civil Engineering (CE) 2025 is part of Civil Engineering (CE) preparation. The Question and answers have been prepared according to the Civil Engineering (CE) exam syllabus. Information about A pipeline conveys 8.23 litre per second of water from an overhead tank to a building. The pipe is 2 km long and 0.15 m in diameter. It is desired to increase the discharge by 30% by installing another pipeline in parallel with this over half the length. Suggest a suitable diameter of the pipe to be installed. Is there any upper limit on discharge augmentation by this arrangement? (Take friction factor f = 0.03. )a) 0.16 m and Qmax = 0.021 m3/sb) 0.17 m and Qmax = 0.012 m3/sc) 0.16 m and Qmax = 0.012 m3/sd) 0.17 m and Qmax = 0.021 m3/sCorrect answer is option 'C'. Can you explain this answer? covers all topics & solutions for Civil Engineering (CE) 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for A pipeline conveys 8.23 litre per second of water from an overhead tank to a building. The pipe is 2 km long and 0.15 m in diameter. It is desired to increase the discharge by 30% by installing another pipeline in parallel with this over half the length. Suggest a suitable diameter of the pipe to be installed. Is there any upper limit on discharge augmentation by this arrangement? (Take friction factor f = 0.03. )a) 0.16 m and Qmax = 0.021 m3/sb) 0.17 m and Qmax = 0.012 m3/sc) 0.16 m and Qmax = 0.012 m3/sd) 0.17 m and Qmax = 0.021 m3/sCorrect answer is option 'C'. Can you explain this answer?.
Solutions for A pipeline conveys 8.23 litre per second of water from an overhead tank to a building. The pipe is 2 km long and 0.15 m in diameter. It is desired to increase the discharge by 30% by installing another pipeline in parallel with this over half the length. Suggest a suitable diameter of the pipe to be installed. Is there any upper limit on discharge augmentation by this arrangement? (Take friction factor f = 0.03. )a) 0.16 m and Qmax = 0.021 m3/sb) 0.17 m and Qmax = 0.012 m3/sc) 0.16 m and Qmax = 0.012 m3/sd) 0.17 m and Qmax = 0.021 m3/sCorrect answer is option 'C'. Can you explain this answer? in English & in Hindi are available as part of our courses for Civil Engineering (CE).
Download more important topics, notes, lectures and mock test series for Civil Engineering (CE) Exam by signing up for free.
Here you can find the meaning of A pipeline conveys 8.23 litre per second of water from an overhead tank to a building. The pipe is 2 km long and 0.15 m in diameter. It is desired to increase the discharge by 30% by installing another pipeline in parallel with this over half the length. Suggest a suitable diameter of the pipe to be installed. Is there any upper limit on discharge augmentation by this arrangement? (Take friction factor f = 0.03. )a) 0.16 m and Qmax = 0.021 m3/sb) 0.17 m and Qmax = 0.012 m3/sc) 0.16 m and Qmax = 0.012 m3/sd) 0.17 m and Qmax = 0.021 m3/sCorrect answer is option 'C'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
A pipeline conveys 8.23 litre per second of water from an overhead tank to a building. The pipe is 2 km long and 0.15 m in diameter. It is desired to increase the discharge by 30% by installing another pipeline in parallel with this over half the length. Suggest a suitable diameter of the pipe to be installed. Is there any upper limit on discharge augmentation by this arrangement? (Take friction factor f = 0.03. )a) 0.16 m and Qmax = 0.021 m3/sb) 0.17 m and Qmax = 0.012 m3/sc) 0.16 m and Qmax = 0.012 m3/sd) 0.17 m and Qmax = 0.021 m3/sCorrect answer is option 'C'. Can you explain this answer?, a detailed solution for A pipeline conveys 8.23 litre per second of water from an overhead tank to a building. The pipe is 2 km long and 0.15 m in diameter. It is desired to increase the discharge by 30% by installing another pipeline in parallel with this over half the length. Suggest a suitable diameter of the pipe to be installed. Is there any upper limit on discharge augmentation by this arrangement? (Take friction factor f = 0.03. )a) 0.16 m and Qmax = 0.021 m3/sb) 0.17 m and Qmax = 0.012 m3/sc) 0.16 m and Qmax = 0.012 m3/sd) 0.17 m and Qmax = 0.021 m3/sCorrect answer is option 'C'. Can you explain this answer? has been provided alongside types of A pipeline conveys 8.23 litre per second of water from an overhead tank to a building. The pipe is 2 km long and 0.15 m in diameter. It is desired to increase the discharge by 30% by installing another pipeline in parallel with this over half the length. Suggest a suitable diameter of the pipe to be installed. Is there any upper limit on discharge augmentation by this arrangement? (Take friction factor f = 0.03. )a) 0.16 m and Qmax = 0.021 m3/sb) 0.17 m and Qmax = 0.012 m3/sc) 0.16 m and Qmax = 0.012 m3/sd) 0.17 m and Qmax = 0.021 m3/sCorrect answer is option 'C'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice A pipeline conveys 8.23 litre per second of water from an overhead tank to a building. The pipe is 2 km long and 0.15 m in diameter. It is desired to increase the discharge by 30% by installing another pipeline in parallel with this over half the length. Suggest a suitable diameter of the pipe to be installed. Is there any upper limit on discharge augmentation by this arrangement? (Take friction factor f = 0.03. )a) 0.16 m and Qmax = 0.021 m3/sb) 0.17 m and Qmax = 0.012 m3/sc) 0.16 m and Qmax = 0.012 m3/sd) 0.17 m and Qmax = 0.021 m3/sCorrect answer is option 'C'. Can you explain this answer? tests, examples and also practice Civil Engineering (CE) tests.

|
Explore Courses for Civil Engineering (CE) exam
|

|
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.


























