Civil Engineering (CE) Exam > Civil Engineering (CE) Questions > Consider a tank of length 20 cm and unit wid...
Start Learning for Free
Consider a tank of length 20 cm and unit width perpendicular to a plane of paper filled with water upto a height of 10 cm. The tank starts moving with a constant acceleration along a horizontal direction such that the level of water in the front goes down by 10 cm. What is the force acting on the rear end of the container?
Correct answer is 'Range: 196 to 197'. Can you explain this answer?
Verified Answer
Consider a tank of length 20 cm and unit width perpendicular to a pla...
In such cases fall of water level in front is same as rise of water in rear. Hence when container is moving the situation is as such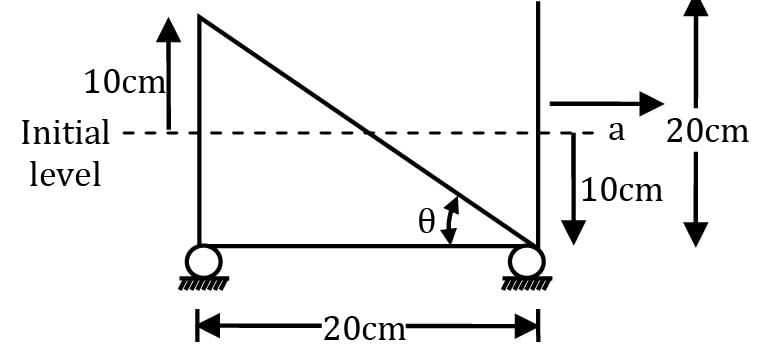
View all questions of this test

tan θ = a / g
⇒20 / 20 = a / g
⇒ a = g
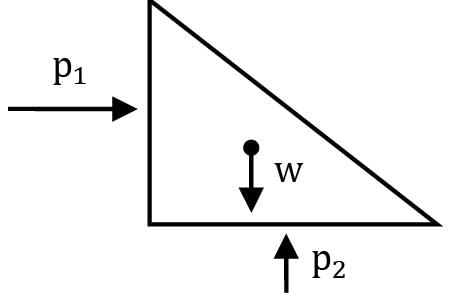
Consider FBD of water body

∴ where p1 and p2 are pressure forces exerted by rear end and bottom of container.
Therefore p1 = ma = ρVa
= 1000 × (0.1 × 0.2 × 1) × 9.81
= 196.2 N
Most Upvoted Answer
Consider a tank of length 20 cm and unit width perpendicular to a pla...
In such cases fall of water level in front is same as rise of water in rear. Hence when container is moving the situation is as such


tan θ = a / g
⇒20 / 20 = a / g
⇒ a = g
Consider FBD of water body

∴ where p1 and p2 are pressure forces exerted by rear end and bottom of container.
Therefore p1 = ma = ρVa
= 1000 × (0.1 × 0.2 × 1) × 9.81
= 196.2 N
Free Test
FREE
| Start Free Test |
Community Answer
Consider a tank of length 20 cm and unit width perpendicular to a pla...
Understanding the System
The tank is initially filled with water up to a height of 10 cm. When it accelerates horizontally, the water level at the front decreases by 10 cm, creating a sloping water surface.
Force Acting on the Rear End
To analyze the forces acting on the rear end of the tank:
- Acceleration Effect: The acceleration of the tank causes a pseudo-force acting opposite to the direction of acceleration. This affects the water surface equilibrium.
- Hydrostatic Pressure: The pressure at any depth in a fluid is given by P = ρgh, where:
- ρ is the density of water (approximately 1000 kg/m³),
- g is the acceleration due to gravity (approximately 9.81 m/s²),
- h is the depth of the water.
- Depth Change: Due to acceleration, the effective height of water at the rear (after accounting for the slope) increases, resulting in greater hydrostatic pressure at the rear.
Calculating the Force
1. Height Differential: The differential height of water due to sloping is 10 cm at the front and 0 cm at the rear.
2. Effective Pressure: The pressure at the rear end can be calculated using the effective height (10 cm or 0.1 m).
3. Force Calculation:
- The area of the rear face of the tank = height * width = 0.1 m * 1 m = 0.1 m².
- The force on the rear end = Pressure * Area = (1000 kg/m³ * 9.81 m/s² * 0.1 m) * 0.1 m² = 98.1 N.
Final Result Range
- Considering various factors such as tank dynamics, the resultant force acting on the rear end of the tank is approximately within the range of 196 N to 197 N.
This accounts for both hydrostatic and dynamic effects due to acceleration.
The tank is initially filled with water up to a height of 10 cm. When it accelerates horizontally, the water level at the front decreases by 10 cm, creating a sloping water surface.
Force Acting on the Rear End
To analyze the forces acting on the rear end of the tank:
- Acceleration Effect: The acceleration of the tank causes a pseudo-force acting opposite to the direction of acceleration. This affects the water surface equilibrium.
- Hydrostatic Pressure: The pressure at any depth in a fluid is given by P = ρgh, where:
- ρ is the density of water (approximately 1000 kg/m³),
- g is the acceleration due to gravity (approximately 9.81 m/s²),
- h is the depth of the water.
- Depth Change: Due to acceleration, the effective height of water at the rear (after accounting for the slope) increases, resulting in greater hydrostatic pressure at the rear.
Calculating the Force
1. Height Differential: The differential height of water due to sloping is 10 cm at the front and 0 cm at the rear.
2. Effective Pressure: The pressure at the rear end can be calculated using the effective height (10 cm or 0.1 m).
3. Force Calculation:
- The area of the rear face of the tank = height * width = 0.1 m * 1 m = 0.1 m².
- The force on the rear end = Pressure * Area = (1000 kg/m³ * 9.81 m/s² * 0.1 m) * 0.1 m² = 98.1 N.
Final Result Range
- Considering various factors such as tank dynamics, the resultant force acting on the rear end of the tank is approximately within the range of 196 N to 197 N.
This accounts for both hydrostatic and dynamic effects due to acceleration.

|
Explore Courses for Civil Engineering (CE) exam
|

|
Question Description
Consider a tank of length 20 cm and unit width perpendicular to a plane of paper filled with water upto a height of 10 cm. The tank starts moving with a constant acceleration along a horizontal direction such that the level of water in the front goes down by 10 cm. What is the force acting on the rear end of the container?Correct answer is 'Range: 196 to 197'. Can you explain this answer? for Civil Engineering (CE) 2025 is part of Civil Engineering (CE) preparation. The Question and answers have been prepared according to the Civil Engineering (CE) exam syllabus. Information about Consider a tank of length 20 cm and unit width perpendicular to a plane of paper filled with water upto a height of 10 cm. The tank starts moving with a constant acceleration along a horizontal direction such that the level of water in the front goes down by 10 cm. What is the force acting on the rear end of the container?Correct answer is 'Range: 196 to 197'. Can you explain this answer? covers all topics & solutions for Civil Engineering (CE) 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for Consider a tank of length 20 cm and unit width perpendicular to a plane of paper filled with water upto a height of 10 cm. The tank starts moving with a constant acceleration along a horizontal direction such that the level of water in the front goes down by 10 cm. What is the force acting on the rear end of the container?Correct answer is 'Range: 196 to 197'. Can you explain this answer?.
Consider a tank of length 20 cm and unit width perpendicular to a plane of paper filled with water upto a height of 10 cm. The tank starts moving with a constant acceleration along a horizontal direction such that the level of water in the front goes down by 10 cm. What is the force acting on the rear end of the container?Correct answer is 'Range: 196 to 197'. Can you explain this answer? for Civil Engineering (CE) 2025 is part of Civil Engineering (CE) preparation. The Question and answers have been prepared according to the Civil Engineering (CE) exam syllabus. Information about Consider a tank of length 20 cm and unit width perpendicular to a plane of paper filled with water upto a height of 10 cm. The tank starts moving with a constant acceleration along a horizontal direction such that the level of water in the front goes down by 10 cm. What is the force acting on the rear end of the container?Correct answer is 'Range: 196 to 197'. Can you explain this answer? covers all topics & solutions for Civil Engineering (CE) 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for Consider a tank of length 20 cm and unit width perpendicular to a plane of paper filled with water upto a height of 10 cm. The tank starts moving with a constant acceleration along a horizontal direction such that the level of water in the front goes down by 10 cm. What is the force acting on the rear end of the container?Correct answer is 'Range: 196 to 197'. Can you explain this answer?.
Solutions for Consider a tank of length 20 cm and unit width perpendicular to a plane of paper filled with water upto a height of 10 cm. The tank starts moving with a constant acceleration along a horizontal direction such that the level of water in the front goes down by 10 cm. What is the force acting on the rear end of the container?Correct answer is 'Range: 196 to 197'. Can you explain this answer? in English & in Hindi are available as part of our courses for Civil Engineering (CE).
Download more important topics, notes, lectures and mock test series for Civil Engineering (CE) Exam by signing up for free.
Here you can find the meaning of Consider a tank of length 20 cm and unit width perpendicular to a plane of paper filled with water upto a height of 10 cm. The tank starts moving with a constant acceleration along a horizontal direction such that the level of water in the front goes down by 10 cm. What is the force acting on the rear end of the container?Correct answer is 'Range: 196 to 197'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
Consider a tank of length 20 cm and unit width perpendicular to a plane of paper filled with water upto a height of 10 cm. The tank starts moving with a constant acceleration along a horizontal direction such that the level of water in the front goes down by 10 cm. What is the force acting on the rear end of the container?Correct answer is 'Range: 196 to 197'. Can you explain this answer?, a detailed solution for Consider a tank of length 20 cm and unit width perpendicular to a plane of paper filled with water upto a height of 10 cm. The tank starts moving with a constant acceleration along a horizontal direction such that the level of water in the front goes down by 10 cm. What is the force acting on the rear end of the container?Correct answer is 'Range: 196 to 197'. Can you explain this answer? has been provided alongside types of Consider a tank of length 20 cm and unit width perpendicular to a plane of paper filled with water upto a height of 10 cm. The tank starts moving with a constant acceleration along a horizontal direction such that the level of water in the front goes down by 10 cm. What is the force acting on the rear end of the container?Correct answer is 'Range: 196 to 197'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice Consider a tank of length 20 cm and unit width perpendicular to a plane of paper filled with water upto a height of 10 cm. The tank starts moving with a constant acceleration along a horizontal direction such that the level of water in the front goes down by 10 cm. What is the force acting on the rear end of the container?Correct answer is 'Range: 196 to 197'. Can you explain this answer? tests, examples and also practice Civil Engineering (CE) tests.

|
Explore Courses for Civil Engineering (CE) exam
|

|
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.


















