Mechanical Engineering Exam > Mechanical Engineering Questions > Consider the following statements Modulus of...
Start Learning for Free
Consider the following statements Modulus of rigidity and bulk modulus of a material are found to be 60 GPa and 140 GPa respectively. Then
1. elasticity modulus is nearly 200 GPa
2. Poisson’s ratio is nearly 0.3
3. elasticity modulus is nearly 158 GPa
4. Poisson’s ratio is nearly 0.25
Which of these statements are correct?
- a)1 and 3
- b)2 and 4
- c)1 and 4
- d)2 and 3
Correct answer is option 'D'. Can you explain this answer?
| FREE This question is part of | Download PDF Attempt this Test |
Verified Answer
Consider the following statements Modulus of rigidity and bulk modulu...
G = 60 GPa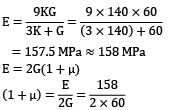
View all questions of this test
K = 140 GPa
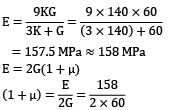
μ = 0.31 ≈ 0.3 Statement 2 and 3 are correct.
Most Upvoted Answer
Consider the following statements Modulus of rigidity and bulk modulu...
To determine the correct statements, let's review the definitions and relationships between the different elastic moduli.
1. Modulus of Rigidity (Shear Modulus): The modulus of rigidity, also known as the shear modulus, measures the resistance of a material to shearing deformation. It is denoted by G and has units of pressure (Pa or N/m²). In this case, the modulus of rigidity is given as 60 GPa (GigaPascals).
2. Bulk Modulus: The bulk modulus measures the resistance of a material to uniform compression or volume change. It is denoted by K and also has units of pressure (Pa or N/m²). In this case, the bulk modulus is given as 140 GPa.
3. Young's Modulus (Elasticity Modulus): Young's modulus, also known as the elasticity modulus, measures the stiffness of a material and its ability to resist linear elastic deformation. It is denoted by E and has units of pressure (Pa or N/m²). Young's modulus can be related to the modulus of rigidity and bulk modulus through the following equations:
Young's modulus (E) = 2 x Modulus of Rigidity (G) x (1 + Poisson's ratio)
Bulk modulus (K) = Young's modulus (E) / (3 x (1 - 2 x Poisson's ratio))
To determine the correct statements, we can use the given values of the modulus of rigidity and bulk modulus and solve for the other parameters.
Let's evaluate each statement:
1. Elasticity modulus is nearly 200 GPa:
Using the equation above, we can rearrange it to solve for Young's modulus (E):
E = 2 x G x (1 + Poisson's ratio)
E = 2 x 60 GPa x (1 + Poisson's ratio)
We don't have the value of Poisson's ratio, so we cannot determine the exact value of Young's modulus. Therefore, statement 1 is incorrect.
2. Poisson's ratio is nearly 0.3:
Since we don't have the value of Poisson's ratio, we cannot determine whether it is approximately 0.3 or not. Therefore, statement 2 is incorrect.
3. Elasticity modulus is nearly 158 GPa:
Using the equation above, we can rearrange it to solve for Young's modulus (E):
E = 2 x G x (1 + Poisson's ratio)
E = 2 x 60 GPa x (1 + Poisson's ratio)
Again, without the value of Poisson's ratio, we cannot determine the exact value of Young's modulus. Therefore, statement 3 is incorrect.
4. Poisson's ratio is nearly 0.25:
Using the equation for the bulk modulus, we can rearrange it to solve for Poisson's ratio:
Poisson's ratio = (1 - (E / (3 x K))) / 2
Substituting the given values, we have:
Poisson's ratio = (1 - (E / (3 x 140 GPa))) / 2
Without knowing the value of Young's modulus, we cannot calculate the exact value of Poisson's ratio. However, we can see that the value of Poisson's ratio will be less than 0.5 since the numerator of the equation is always positive. Therefore,
1. Modulus of Rigidity (Shear Modulus): The modulus of rigidity, also known as the shear modulus, measures the resistance of a material to shearing deformation. It is denoted by G and has units of pressure (Pa or N/m²). In this case, the modulus of rigidity is given as 60 GPa (GigaPascals).
2. Bulk Modulus: The bulk modulus measures the resistance of a material to uniform compression or volume change. It is denoted by K and also has units of pressure (Pa or N/m²). In this case, the bulk modulus is given as 140 GPa.
3. Young's Modulus (Elasticity Modulus): Young's modulus, also known as the elasticity modulus, measures the stiffness of a material and its ability to resist linear elastic deformation. It is denoted by E and has units of pressure (Pa or N/m²). Young's modulus can be related to the modulus of rigidity and bulk modulus through the following equations:
Young's modulus (E) = 2 x Modulus of Rigidity (G) x (1 + Poisson's ratio)
Bulk modulus (K) = Young's modulus (E) / (3 x (1 - 2 x Poisson's ratio))
To determine the correct statements, we can use the given values of the modulus of rigidity and bulk modulus and solve for the other parameters.
Let's evaluate each statement:
1. Elasticity modulus is nearly 200 GPa:
Using the equation above, we can rearrange it to solve for Young's modulus (E):
E = 2 x G x (1 + Poisson's ratio)
E = 2 x 60 GPa x (1 + Poisson's ratio)
We don't have the value of Poisson's ratio, so we cannot determine the exact value of Young's modulus. Therefore, statement 1 is incorrect.
2. Poisson's ratio is nearly 0.3:
Since we don't have the value of Poisson's ratio, we cannot determine whether it is approximately 0.3 or not. Therefore, statement 2 is incorrect.
3. Elasticity modulus is nearly 158 GPa:
Using the equation above, we can rearrange it to solve for Young's modulus (E):
E = 2 x G x (1 + Poisson's ratio)
E = 2 x 60 GPa x (1 + Poisson's ratio)
Again, without the value of Poisson's ratio, we cannot determine the exact value of Young's modulus. Therefore, statement 3 is incorrect.
4. Poisson's ratio is nearly 0.25:
Using the equation for the bulk modulus, we can rearrange it to solve for Poisson's ratio:
Poisson's ratio = (1 - (E / (3 x K))) / 2
Substituting the given values, we have:
Poisson's ratio = (1 - (E / (3 x 140 GPa))) / 2
Without knowing the value of Young's modulus, we cannot calculate the exact value of Poisson's ratio. However, we can see that the value of Poisson's ratio will be less than 0.5 since the numerator of the equation is always positive. Therefore,
Attention Mechanical Engineering Students!
To make sure you are not studying endlessly, EduRev has designed Mechanical Engineering study material, with Structured Courses, Videos, & Test Series. Plus get personalized analysis, doubt solving and improvement plans to achieve a great score in Mechanical Engineering.
|
Explore Courses for Mechanical Engineering exam
|
|
Similar Mechanical Engineering Doubts
Top Courses for Mechanical EngineeringView all
Consider the following statements Modulus of rigidity and bulk modulus of a material are found to be 60 GPa and 140 GPa respectively. Then1. elasticity modulus is nearly 200 GPa2. Poisson’s ratio is nearly 0.33. elasticity modulus is nearly 158 GPa4. Poisson’s ratio is nearly 0.25Which of these statements are correct?a) 1 and 3b) 2 and 4c) 1 and 4d) 2 and 3Correct answer is option 'D'. Can you explain this answer?
Question Description
Consider the following statements Modulus of rigidity and bulk modulus of a material are found to be 60 GPa and 140 GPa respectively. Then1. elasticity modulus is nearly 200 GPa2. Poisson’s ratio is nearly 0.33. elasticity modulus is nearly 158 GPa4. Poisson’s ratio is nearly 0.25Which of these statements are correct?a) 1 and 3b) 2 and 4c) 1 and 4d) 2 and 3Correct answer is option 'D'. Can you explain this answer? for Mechanical Engineering 2024 is part of Mechanical Engineering preparation. The Question and answers have been prepared according to the Mechanical Engineering exam syllabus. Information about Consider the following statements Modulus of rigidity and bulk modulus of a material are found to be 60 GPa and 140 GPa respectively. Then1. elasticity modulus is nearly 200 GPa2. Poisson’s ratio is nearly 0.33. elasticity modulus is nearly 158 GPa4. Poisson’s ratio is nearly 0.25Which of these statements are correct?a) 1 and 3b) 2 and 4c) 1 and 4d) 2 and 3Correct answer is option 'D'. Can you explain this answer? covers all topics & solutions for Mechanical Engineering 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for Consider the following statements Modulus of rigidity and bulk modulus of a material are found to be 60 GPa and 140 GPa respectively. Then1. elasticity modulus is nearly 200 GPa2. Poisson’s ratio is nearly 0.33. elasticity modulus is nearly 158 GPa4. Poisson’s ratio is nearly 0.25Which of these statements are correct?a) 1 and 3b) 2 and 4c) 1 and 4d) 2 and 3Correct answer is option 'D'. Can you explain this answer?.
Consider the following statements Modulus of rigidity and bulk modulus of a material are found to be 60 GPa and 140 GPa respectively. Then1. elasticity modulus is nearly 200 GPa2. Poisson’s ratio is nearly 0.33. elasticity modulus is nearly 158 GPa4. Poisson’s ratio is nearly 0.25Which of these statements are correct?a) 1 and 3b) 2 and 4c) 1 and 4d) 2 and 3Correct answer is option 'D'. Can you explain this answer? for Mechanical Engineering 2024 is part of Mechanical Engineering preparation. The Question and answers have been prepared according to the Mechanical Engineering exam syllabus. Information about Consider the following statements Modulus of rigidity and bulk modulus of a material are found to be 60 GPa and 140 GPa respectively. Then1. elasticity modulus is nearly 200 GPa2. Poisson’s ratio is nearly 0.33. elasticity modulus is nearly 158 GPa4. Poisson’s ratio is nearly 0.25Which of these statements are correct?a) 1 and 3b) 2 and 4c) 1 and 4d) 2 and 3Correct answer is option 'D'. Can you explain this answer? covers all topics & solutions for Mechanical Engineering 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for Consider the following statements Modulus of rigidity and bulk modulus of a material are found to be 60 GPa and 140 GPa respectively. Then1. elasticity modulus is nearly 200 GPa2. Poisson’s ratio is nearly 0.33. elasticity modulus is nearly 158 GPa4. Poisson’s ratio is nearly 0.25Which of these statements are correct?a) 1 and 3b) 2 and 4c) 1 and 4d) 2 and 3Correct answer is option 'D'. Can you explain this answer?.
Solutions for Consider the following statements Modulus of rigidity and bulk modulus of a material are found to be 60 GPa and 140 GPa respectively. Then1. elasticity modulus is nearly 200 GPa2. Poisson’s ratio is nearly 0.33. elasticity modulus is nearly 158 GPa4. Poisson’s ratio is nearly 0.25Which of these statements are correct?a) 1 and 3b) 2 and 4c) 1 and 4d) 2 and 3Correct answer is option 'D'. Can you explain this answer? in English & in Hindi are available as part of our courses for Mechanical Engineering.
Download more important topics, notes, lectures and mock test series for Mechanical Engineering Exam by signing up for free.
Here you can find the meaning of Consider the following statements Modulus of rigidity and bulk modulus of a material are found to be 60 GPa and 140 GPa respectively. Then1. elasticity modulus is nearly 200 GPa2. Poisson’s ratio is nearly 0.33. elasticity modulus is nearly 158 GPa4. Poisson’s ratio is nearly 0.25Which of these statements are correct?a) 1 and 3b) 2 and 4c) 1 and 4d) 2 and 3Correct answer is option 'D'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
Consider the following statements Modulus of rigidity and bulk modulus of a material are found to be 60 GPa and 140 GPa respectively. Then1. elasticity modulus is nearly 200 GPa2. Poisson’s ratio is nearly 0.33. elasticity modulus is nearly 158 GPa4. Poisson’s ratio is nearly 0.25Which of these statements are correct?a) 1 and 3b) 2 and 4c) 1 and 4d) 2 and 3Correct answer is option 'D'. Can you explain this answer?, a detailed solution for Consider the following statements Modulus of rigidity and bulk modulus of a material are found to be 60 GPa and 140 GPa respectively. Then1. elasticity modulus is nearly 200 GPa2. Poisson’s ratio is nearly 0.33. elasticity modulus is nearly 158 GPa4. Poisson’s ratio is nearly 0.25Which of these statements are correct?a) 1 and 3b) 2 and 4c) 1 and 4d) 2 and 3Correct answer is option 'D'. Can you explain this answer? has been provided alongside types of Consider the following statements Modulus of rigidity and bulk modulus of a material are found to be 60 GPa and 140 GPa respectively. Then1. elasticity modulus is nearly 200 GPa2. Poisson’s ratio is nearly 0.33. elasticity modulus is nearly 158 GPa4. Poisson’s ratio is nearly 0.25Which of these statements are correct?a) 1 and 3b) 2 and 4c) 1 and 4d) 2 and 3Correct answer is option 'D'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice Consider the following statements Modulus of rigidity and bulk modulus of a material are found to be 60 GPa and 140 GPa respectively. Then1. elasticity modulus is nearly 200 GPa2. Poisson’s ratio is nearly 0.33. elasticity modulus is nearly 158 GPa4. Poisson’s ratio is nearly 0.25Which of these statements are correct?a) 1 and 3b) 2 and 4c) 1 and 4d) 2 and 3Correct answer is option 'D'. Can you explain this answer? tests, examples and also practice Mechanical Engineering tests.
|
|
Explore Courses for Mechanical Engineering exam
|
|
Suggested Free Tests
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.
|
© EduRev
|
Education Revolution
|
Follow Us
|
Signup to see your scores
go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup