Mechanical Engineering Exam > Mechanical Engineering Questions > In a convective heat transfer situation Reyno...
Start Learning for Free
In a convective heat transfer situation Reynolds number (Re) is very large but the Prandtl number (Pr) is so small that the product of Re and Pr is less than one. In such a condition which one of the following is correct?
- a)Thermal boundary layer does not exist
- b)Viscous boundary layer thickness is less than the thermal boundary layer thickness
- c)Viscous boundary layer thickness is equal to the thermal boundary layer thickness
- d)Viscous boundary layer thickness is greater than the thermal boundary layer thickness
Correct answer is option 'B'. Can you explain this answer?
| FREE This question is part of | Download PDF Attempt this Test |
Verified Answer
In a convective heat transfer situation Reynolds number (Re) is very l...
When Pr number is less than one. The Reynold number only signifies about the thickness of the hydrodynamic boundary layer and related to thermal boundary through the Prandtl number.
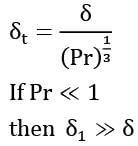
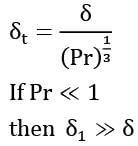
Most Upvoted Answer
In a convective heat transfer situation Reynolds number (Re) is very l...
Explanation:
In a convective heat transfer situation, the Reynolds number (Re) is a dimensionless quantity that characterizes the flow of a fluid. It is defined as the ratio of inertial forces to viscous forces and is given by the equation:
Re = (ρuL) / μ
Where:
- ρ is the density of the fluid
- u is the velocity of the fluid
- L is a characteristic length of the flow
- μ is the dynamic viscosity of the fluid
On the other hand, the Prandtl number (Pr) is another dimensionless quantity that characterizes the relative importance of momentum diffusion (viscous forces) to thermal diffusion (conductive heat transfer) in a fluid. It is given by the equation:
Pr = μCp / k
Where:
- Cp is the specific heat capacity of the fluid at constant pressure
- k is the thermal conductivity of the fluid
Product of Re and Pr:
The product of Reynolds number (Re) and Prandtl number (Pr) is an important parameter in heat transfer analysis. It is given by the equation:
RePr = (ρuL) / (μCp / k)
Simplifying the equation, we get:
RePr = ρuL^2Cp / μk
Condition given in the question:
According to the condition given in the question, the Reynolds number (Re) is very large but the Prandtl number (Pr) is so small that the product of Re and Pr is less than one. Mathematically, this can be written as:
RePr < />
Effect on boundary layer thickness:
The boundary layer is a thin layer of fluid in the immediate vicinity of a solid surface where the fluid velocity and temperature gradients are significant. In convective heat transfer, there are two types of boundary layers: thermal boundary layer and viscous boundary layer.
- Thermal boundary layer: The thermal boundary layer is the region where the temperature gradient is significant. It is influenced by the thermal conductivity of the fluid.
- Viscous boundary layer: The viscous boundary layer is the region where the velocity gradient is significant. It is influenced by the dynamic viscosity of the fluid.
Conclusion:
Based on the given condition, where RePr < 1,="" it="" implies="" that="" the="" product="" of="" the="" reynolds="" number="" and="" prandtl="" number="" is="" small.="" this="" indicates="" that="" the="" viscous="" forces="" dominate="" over="" the="" thermal="" diffusion="" in="" the="" flow.="" consequently,="" the="" viscous="" boundary="" layer="" thickness="" is="" smaller="" than="" the="" thermal="" boundary="" layer="" thickness.="" therefore,="" option="" 'b'="" is="" the="" correct="" answer.="" 1,="" it="" implies="" that="" the="" product="" of="" the="" reynolds="" number="" and="" prandtl="" number="" is="" small.="" this="" indicates="" that="" the="" viscous="" forces="" dominate="" over="" the="" thermal="" diffusion="" in="" the="" flow.="" consequently,="" the="" viscous="" boundary="" layer="" thickness="" is="" smaller="" than="" the="" thermal="" boundary="" layer="" thickness.="" therefore,="" option="" 'b'="" is="" the="" correct="" />
In a convective heat transfer situation, the Reynolds number (Re) is a dimensionless quantity that characterizes the flow of a fluid. It is defined as the ratio of inertial forces to viscous forces and is given by the equation:
Re = (ρuL) / μ
Where:
- ρ is the density of the fluid
- u is the velocity of the fluid
- L is a characteristic length of the flow
- μ is the dynamic viscosity of the fluid
On the other hand, the Prandtl number (Pr) is another dimensionless quantity that characterizes the relative importance of momentum diffusion (viscous forces) to thermal diffusion (conductive heat transfer) in a fluid. It is given by the equation:
Pr = μCp / k
Where:
- Cp is the specific heat capacity of the fluid at constant pressure
- k is the thermal conductivity of the fluid
Product of Re and Pr:
The product of Reynolds number (Re) and Prandtl number (Pr) is an important parameter in heat transfer analysis. It is given by the equation:
RePr = (ρuL) / (μCp / k)
Simplifying the equation, we get:
RePr = ρuL^2Cp / μk
Condition given in the question:
According to the condition given in the question, the Reynolds number (Re) is very large but the Prandtl number (Pr) is so small that the product of Re and Pr is less than one. Mathematically, this can be written as:
RePr < />
Effect on boundary layer thickness:
The boundary layer is a thin layer of fluid in the immediate vicinity of a solid surface where the fluid velocity and temperature gradients are significant. In convective heat transfer, there are two types of boundary layers: thermal boundary layer and viscous boundary layer.
- Thermal boundary layer: The thermal boundary layer is the region where the temperature gradient is significant. It is influenced by the thermal conductivity of the fluid.
- Viscous boundary layer: The viscous boundary layer is the region where the velocity gradient is significant. It is influenced by the dynamic viscosity of the fluid.
Conclusion:
Based on the given condition, where RePr < 1,="" it="" implies="" that="" the="" product="" of="" the="" reynolds="" number="" and="" prandtl="" number="" is="" small.="" this="" indicates="" that="" the="" viscous="" forces="" dominate="" over="" the="" thermal="" diffusion="" in="" the="" flow.="" consequently,="" the="" viscous="" boundary="" layer="" thickness="" is="" smaller="" than="" the="" thermal="" boundary="" layer="" thickness.="" therefore,="" option="" 'b'="" is="" the="" correct="" answer.="" 1,="" it="" implies="" that="" the="" product="" of="" the="" reynolds="" number="" and="" prandtl="" number="" is="" small.="" this="" indicates="" that="" the="" viscous="" forces="" dominate="" over="" the="" thermal="" diffusion="" in="" the="" flow.="" consequently,="" the="" viscous="" boundary="" layer="" thickness="" is="" smaller="" than="" the="" thermal="" boundary="" layer="" thickness.="" therefore,="" option="" 'b'="" is="" the="" correct="" />
Attention Mechanical Engineering Students!
To make sure you are not studying endlessly, EduRev has designed Mechanical Engineering study material, with Structured Courses, Videos, & Test Series. Plus get personalized analysis, doubt solving and improvement plans to achieve a great score in Mechanical Engineering.

|
Explore Courses for Mechanical Engineering exam
|

|
Similar Mechanical Engineering Doubts
In a convective heat transfer situation Reynolds number (Re) is very large but the Prandtl number (Pr) is so small that the product of Re and Pr is less than one. In such a condition which one of the following is correct?a)Thermal boundary layer does not existb)Viscous boundary layer thickness is less than the thermal boundary layer thicknessc)Viscous boundary layer thickness is equal to the thermal boundary layer thicknessd)Viscous boundary layer thickness is greater than the thermal boundary layer thicknessCorrect answer is option 'B'. Can you explain this answer?
Question Description
In a convective heat transfer situation Reynolds number (Re) is very large but the Prandtl number (Pr) is so small that the product of Re and Pr is less than one. In such a condition which one of the following is correct?a)Thermal boundary layer does not existb)Viscous boundary layer thickness is less than the thermal boundary layer thicknessc)Viscous boundary layer thickness is equal to the thermal boundary layer thicknessd)Viscous boundary layer thickness is greater than the thermal boundary layer thicknessCorrect answer is option 'B'. Can you explain this answer? for Mechanical Engineering 2024 is part of Mechanical Engineering preparation. The Question and answers have been prepared according to the Mechanical Engineering exam syllabus. Information about In a convective heat transfer situation Reynolds number (Re) is very large but the Prandtl number (Pr) is so small that the product of Re and Pr is less than one. In such a condition which one of the following is correct?a)Thermal boundary layer does not existb)Viscous boundary layer thickness is less than the thermal boundary layer thicknessc)Viscous boundary layer thickness is equal to the thermal boundary layer thicknessd)Viscous boundary layer thickness is greater than the thermal boundary layer thicknessCorrect answer is option 'B'. Can you explain this answer? covers all topics & solutions for Mechanical Engineering 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for In a convective heat transfer situation Reynolds number (Re) is very large but the Prandtl number (Pr) is so small that the product of Re and Pr is less than one. In such a condition which one of the following is correct?a)Thermal boundary layer does not existb)Viscous boundary layer thickness is less than the thermal boundary layer thicknessc)Viscous boundary layer thickness is equal to the thermal boundary layer thicknessd)Viscous boundary layer thickness is greater than the thermal boundary layer thicknessCorrect answer is option 'B'. Can you explain this answer?.
In a convective heat transfer situation Reynolds number (Re) is very large but the Prandtl number (Pr) is so small that the product of Re and Pr is less than one. In such a condition which one of the following is correct?a)Thermal boundary layer does not existb)Viscous boundary layer thickness is less than the thermal boundary layer thicknessc)Viscous boundary layer thickness is equal to the thermal boundary layer thicknessd)Viscous boundary layer thickness is greater than the thermal boundary layer thicknessCorrect answer is option 'B'. Can you explain this answer? for Mechanical Engineering 2024 is part of Mechanical Engineering preparation. The Question and answers have been prepared according to the Mechanical Engineering exam syllabus. Information about In a convective heat transfer situation Reynolds number (Re) is very large but the Prandtl number (Pr) is so small that the product of Re and Pr is less than one. In such a condition which one of the following is correct?a)Thermal boundary layer does not existb)Viscous boundary layer thickness is less than the thermal boundary layer thicknessc)Viscous boundary layer thickness is equal to the thermal boundary layer thicknessd)Viscous boundary layer thickness is greater than the thermal boundary layer thicknessCorrect answer is option 'B'. Can you explain this answer? covers all topics & solutions for Mechanical Engineering 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for In a convective heat transfer situation Reynolds number (Re) is very large but the Prandtl number (Pr) is so small that the product of Re and Pr is less than one. In such a condition which one of the following is correct?a)Thermal boundary layer does not existb)Viscous boundary layer thickness is less than the thermal boundary layer thicknessc)Viscous boundary layer thickness is equal to the thermal boundary layer thicknessd)Viscous boundary layer thickness is greater than the thermal boundary layer thicknessCorrect answer is option 'B'. Can you explain this answer?.
Solutions for In a convective heat transfer situation Reynolds number (Re) is very large but the Prandtl number (Pr) is so small that the product of Re and Pr is less than one. In such a condition which one of the following is correct?a)Thermal boundary layer does not existb)Viscous boundary layer thickness is less than the thermal boundary layer thicknessc)Viscous boundary layer thickness is equal to the thermal boundary layer thicknessd)Viscous boundary layer thickness is greater than the thermal boundary layer thicknessCorrect answer is option 'B'. Can you explain this answer? in English & in Hindi are available as part of our courses for Mechanical Engineering.
Download more important topics, notes, lectures and mock test series for Mechanical Engineering Exam by signing up for free.
Here you can find the meaning of In a convective heat transfer situation Reynolds number (Re) is very large but the Prandtl number (Pr) is so small that the product of Re and Pr is less than one. In such a condition which one of the following is correct?a)Thermal boundary layer does not existb)Viscous boundary layer thickness is less than the thermal boundary layer thicknessc)Viscous boundary layer thickness is equal to the thermal boundary layer thicknessd)Viscous boundary layer thickness is greater than the thermal boundary layer thicknessCorrect answer is option 'B'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
In a convective heat transfer situation Reynolds number (Re) is very large but the Prandtl number (Pr) is so small that the product of Re and Pr is less than one. In such a condition which one of the following is correct?a)Thermal boundary layer does not existb)Viscous boundary layer thickness is less than the thermal boundary layer thicknessc)Viscous boundary layer thickness is equal to the thermal boundary layer thicknessd)Viscous boundary layer thickness is greater than the thermal boundary layer thicknessCorrect answer is option 'B'. Can you explain this answer?, a detailed solution for In a convective heat transfer situation Reynolds number (Re) is very large but the Prandtl number (Pr) is so small that the product of Re and Pr is less than one. In such a condition which one of the following is correct?a)Thermal boundary layer does not existb)Viscous boundary layer thickness is less than the thermal boundary layer thicknessc)Viscous boundary layer thickness is equal to the thermal boundary layer thicknessd)Viscous boundary layer thickness is greater than the thermal boundary layer thicknessCorrect answer is option 'B'. Can you explain this answer? has been provided alongside types of In a convective heat transfer situation Reynolds number (Re) is very large but the Prandtl number (Pr) is so small that the product of Re and Pr is less than one. In such a condition which one of the following is correct?a)Thermal boundary layer does not existb)Viscous boundary layer thickness is less than the thermal boundary layer thicknessc)Viscous boundary layer thickness is equal to the thermal boundary layer thicknessd)Viscous boundary layer thickness is greater than the thermal boundary layer thicknessCorrect answer is option 'B'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice In a convective heat transfer situation Reynolds number (Re) is very large but the Prandtl number (Pr) is so small that the product of Re and Pr is less than one. In such a condition which one of the following is correct?a)Thermal boundary layer does not existb)Viscous boundary layer thickness is less than the thermal boundary layer thicknessc)Viscous boundary layer thickness is equal to the thermal boundary layer thicknessd)Viscous boundary layer thickness is greater than the thermal boundary layer thicknessCorrect answer is option 'B'. Can you explain this answer? tests, examples and also practice Mechanical Engineering tests.

|
Explore Courses for Mechanical Engineering exam
|

|
Suggested Free Tests
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.
























