Chemical Engineering Exam > Chemical Engineering Questions > Consider radial steady state heat conduction...
Start Learning for Free
Consider radial steady state heat conduction through a hollow spherical conductor carrying a heat source inside the sphere. The temperature distribution in the shell T = T (r ) is __________
T is the temperature at a distance r from the center.
- a)linear
- b)parabolic
- c)hyperbolic
- d)logarithmic
Correct answer is option 'C'. Can you explain this answer?
| FREE This question is part of | Download PDF Attempt this Test |
Verified Answer
Consider radial steady state heat conduction through a hollow spheric...
In the question, the sphere is carrying a heat source.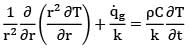
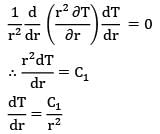
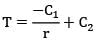
View all questions of this test
General heat conduction equation in spherical coordinates is given as
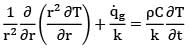
Based on conditions of the question, the equation is reduced to
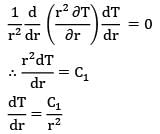
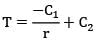
Thus T and r follow a hyperbolic relationship.
Most Upvoted Answer
Consider radial steady state heat conduction through a hollow spheric...
In the question, the sphere is carrying a heat source.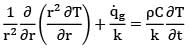
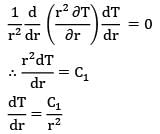
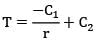
General heat conduction equation in spherical coordinates is given as
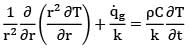
Based on conditions of the question, the equation is reduced to
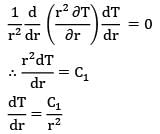
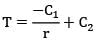
Thus T and r follow a hyperbolic relationship.
Free Test
FREE
| Start Free Test |
Community Answer
Consider radial steady state heat conduction through a hollow spheric...
Radial steady-state heat conduction refers to the transfer of heat through a solid object from the center to the outer surface, with a constant temperature distribution over time. In this case, we have a hollow spherical conductor with a heat source inside the sphere.
The temperature distribution in the shell, denoted as T = T(r), represents the temperature at a distance r from the center of the sphere. We need to determine the nature of this temperature distribution.
To analyze the heat conduction in a hollow spherical conductor, we can apply the radial form of the heat conduction equation, which is given by:
d²T/dr² + (2/r) * dT/dr = 0
The general solution to this equation is given by:
T(r) = A * ln(r) + B
where A and B are constants determined by the boundary conditions.
Now, let's consider the boundary conditions for this problem. At the inner surface of the sphere (r = R₁), the temperature is T₁, and at the outer surface (r = R₂), the temperature is T₂. Since there is a heat source inside the sphere, the temperature will increase as we move from the inner to the outer surface.
At the inner surface, we have:
T(R₁) = T₁ = A * ln(R₁) + B
At the outer surface, we have:
T(R₂) = T₂ = A * ln(R₂) + B
To determine the constants A and B, we can subtract these two equations, which gives:
T₂ - T₁ = A * (ln(R₂) - ln(R₁))
Simplifying this equation, we have:
A = (T₂ - T₁) / (ln(R₂) - ln(R₁))
Substituting the value of A back into the equation for T(r), we have:
T(r) = [(T₂ - T₁) / (ln(R₂) - ln(R₁))] * ln(r) + B
Since ln(r) is present in the equation, the temperature distribution T(r) is hyperbolic, as given by option C.
Therefore, the correct answer is option C: hyperbolic.
The temperature distribution in the shell, denoted as T = T(r), represents the temperature at a distance r from the center of the sphere. We need to determine the nature of this temperature distribution.
To analyze the heat conduction in a hollow spherical conductor, we can apply the radial form of the heat conduction equation, which is given by:
d²T/dr² + (2/r) * dT/dr = 0
The general solution to this equation is given by:
T(r) = A * ln(r) + B
where A and B are constants determined by the boundary conditions.
Now, let's consider the boundary conditions for this problem. At the inner surface of the sphere (r = R₁), the temperature is T₁, and at the outer surface (r = R₂), the temperature is T₂. Since there is a heat source inside the sphere, the temperature will increase as we move from the inner to the outer surface.
At the inner surface, we have:
T(R₁) = T₁ = A * ln(R₁) + B
At the outer surface, we have:
T(R₂) = T₂ = A * ln(R₂) + B
To determine the constants A and B, we can subtract these two equations, which gives:
T₂ - T₁ = A * (ln(R₂) - ln(R₁))
Simplifying this equation, we have:
A = (T₂ - T₁) / (ln(R₂) - ln(R₁))
Substituting the value of A back into the equation for T(r), we have:
T(r) = [(T₂ - T₁) / (ln(R₂) - ln(R₁))] * ln(r) + B
Since ln(r) is present in the equation, the temperature distribution T(r) is hyperbolic, as given by option C.
Therefore, the correct answer is option C: hyperbolic.
|
Explore Courses for Chemical Engineering exam
|
|
Consider radial steady state heat conduction through a hollow spherical conductor carrying a heat source inside the sphere. The temperature distribution in the shell T = T (r ) is __________T is the temperature at a distance r from the center.a) linearb) parabolicc) hyperbolicd) logarithmicCorrect answer is option 'C'. Can you explain this answer?
Question Description
Consider radial steady state heat conduction through a hollow spherical conductor carrying a heat source inside the sphere. The temperature distribution in the shell T = T (r ) is __________T is the temperature at a distance r from the center.a) linearb) parabolicc) hyperbolicd) logarithmicCorrect answer is option 'C'. Can you explain this answer? for Chemical Engineering 2024 is part of Chemical Engineering preparation. The Question and answers have been prepared according to the Chemical Engineering exam syllabus. Information about Consider radial steady state heat conduction through a hollow spherical conductor carrying a heat source inside the sphere. The temperature distribution in the shell T = T (r ) is __________T is the temperature at a distance r from the center.a) linearb) parabolicc) hyperbolicd) logarithmicCorrect answer is option 'C'. Can you explain this answer? covers all topics & solutions for Chemical Engineering 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for Consider radial steady state heat conduction through a hollow spherical conductor carrying a heat source inside the sphere. The temperature distribution in the shell T = T (r ) is __________T is the temperature at a distance r from the center.a) linearb) parabolicc) hyperbolicd) logarithmicCorrect answer is option 'C'. Can you explain this answer?.
Consider radial steady state heat conduction through a hollow spherical conductor carrying a heat source inside the sphere. The temperature distribution in the shell T = T (r ) is __________T is the temperature at a distance r from the center.a) linearb) parabolicc) hyperbolicd) logarithmicCorrect answer is option 'C'. Can you explain this answer? for Chemical Engineering 2024 is part of Chemical Engineering preparation. The Question and answers have been prepared according to the Chemical Engineering exam syllabus. Information about Consider radial steady state heat conduction through a hollow spherical conductor carrying a heat source inside the sphere. The temperature distribution in the shell T = T (r ) is __________T is the temperature at a distance r from the center.a) linearb) parabolicc) hyperbolicd) logarithmicCorrect answer is option 'C'. Can you explain this answer? covers all topics & solutions for Chemical Engineering 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for Consider radial steady state heat conduction through a hollow spherical conductor carrying a heat source inside the sphere. The temperature distribution in the shell T = T (r ) is __________T is the temperature at a distance r from the center.a) linearb) parabolicc) hyperbolicd) logarithmicCorrect answer is option 'C'. Can you explain this answer?.
Solutions for Consider radial steady state heat conduction through a hollow spherical conductor carrying a heat source inside the sphere. The temperature distribution in the shell T = T (r ) is __________T is the temperature at a distance r from the center.a) linearb) parabolicc) hyperbolicd) logarithmicCorrect answer is option 'C'. Can you explain this answer? in English & in Hindi are available as part of our courses for Chemical Engineering.
Download more important topics, notes, lectures and mock test series for Chemical Engineering Exam by signing up for free.
Here you can find the meaning of Consider radial steady state heat conduction through a hollow spherical conductor carrying a heat source inside the sphere. The temperature distribution in the shell T = T (r ) is __________T is the temperature at a distance r from the center.a) linearb) parabolicc) hyperbolicd) logarithmicCorrect answer is option 'C'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
Consider radial steady state heat conduction through a hollow spherical conductor carrying a heat source inside the sphere. The temperature distribution in the shell T = T (r ) is __________T is the temperature at a distance r from the center.a) linearb) parabolicc) hyperbolicd) logarithmicCorrect answer is option 'C'. Can you explain this answer?, a detailed solution for Consider radial steady state heat conduction through a hollow spherical conductor carrying a heat source inside the sphere. The temperature distribution in the shell T = T (r ) is __________T is the temperature at a distance r from the center.a) linearb) parabolicc) hyperbolicd) logarithmicCorrect answer is option 'C'. Can you explain this answer? has been provided alongside types of Consider radial steady state heat conduction through a hollow spherical conductor carrying a heat source inside the sphere. The temperature distribution in the shell T = T (r ) is __________T is the temperature at a distance r from the center.a) linearb) parabolicc) hyperbolicd) logarithmicCorrect answer is option 'C'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice Consider radial steady state heat conduction through a hollow spherical conductor carrying a heat source inside the sphere. The temperature distribution in the shell T = T (r ) is __________T is the temperature at a distance r from the center.a) linearb) parabolicc) hyperbolicd) logarithmicCorrect answer is option 'C'. Can you explain this answer? tests, examples and also practice Chemical Engineering tests.
|
|
Explore Courses for Chemical Engineering exam
|
|
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.
|
© EduRev
|
Education Revolution
|
Follow Us
|
Signup to see your scores
go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup