Mechanical Engineering Exam > Mechanical Engineering Questions > If the load on a ball bearing is reduced to ...
Start Learning for Free
If the load on a ball bearing is reduced to half, the life of the ball bearing will be B
- a)increases 8 times
- b)increases 16 times
- c)increases 2 times
- d)increases 4 times
Correct answer is option 'A'. Can you explain this answer?
Verified Answer
If the load on a ball bearing is reduced to half, the life of the bal...
Given, Initially, w1 = w
Life = L1
After half of load, w2 =w/2
Life = L2
Considering the relation,
Lw3 = c
L2 = 8L1  times
times
 times
timesMost Upvoted Answer
If the load on a ball bearing is reduced to half, the life of the bal...
To understand why the life of a ball bearing increases 8 times when the load is reduced to half, we need to consider the basic principles of bearing design and operation.
1. Introduction:
- Ball bearings are mechanical components that reduce friction between moving parts.
- They consist of an inner and outer ring, with steel balls sandwiched between them.
- The balls roll between the inner and outer raceways, reducing friction and enabling smooth rotation.
2. Load and Life Relationship:
- The load on a ball bearing refers to the force applied to the bearing during operation.
- Excessive load can cause wear, fatigue, and eventual failure of the bearing.
- The life of a bearing refers to the duration it can operate before failure occurs.
- The relationship between load and life can be described by the bearing life equation, known as the L10 life.
3. L10 Life Equation:
- The L10 life equation calculates the life of a ball bearing in terms of the number of revolutions it can endure before failure.
- The equation is given by L10 = (C/P)^3 x 10^6, where L10 is the rated life, C is the dynamic load rating, and P is the equivalent dynamic bearing load.
4. Load Reduction:
- When the load on a ball bearing is reduced to half, the equivalent dynamic bearing load (P) also reduces by half.
- Since load is directly proportional to the third power in the L10 life equation, reducing the load by half will result in a life increase of 1/2^3 = 1/8.
- Therefore, the life of the ball bearing increases 8 times when the load is reduced to half.
5. Practical Example:
- Suppose a ball bearing has a rated life of 10,000 hours under a given load condition.
- If the load is reduced to half, the new life of the bearing can be calculated using the L10 life equation.
- Assuming all other factors remain constant, the new life will be 8 times the original life, i.e., 8 x 10,000 = 80,000 hours.
In conclusion, reducing the load on a ball bearing to half results in a significant increase in its life. This is due to the relationship between load and life described by the L10 life equation, which shows that reducing the load by half increases the life of the bearing by 8 times.
1. Introduction:
- Ball bearings are mechanical components that reduce friction between moving parts.
- They consist of an inner and outer ring, with steel balls sandwiched between them.
- The balls roll between the inner and outer raceways, reducing friction and enabling smooth rotation.
2. Load and Life Relationship:
- The load on a ball bearing refers to the force applied to the bearing during operation.
- Excessive load can cause wear, fatigue, and eventual failure of the bearing.
- The life of a bearing refers to the duration it can operate before failure occurs.
- The relationship between load and life can be described by the bearing life equation, known as the L10 life.
3. L10 Life Equation:
- The L10 life equation calculates the life of a ball bearing in terms of the number of revolutions it can endure before failure.
- The equation is given by L10 = (C/P)^3 x 10^6, where L10 is the rated life, C is the dynamic load rating, and P is the equivalent dynamic bearing load.
4. Load Reduction:
- When the load on a ball bearing is reduced to half, the equivalent dynamic bearing load (P) also reduces by half.
- Since load is directly proportional to the third power in the L10 life equation, reducing the load by half will result in a life increase of 1/2^3 = 1/8.
- Therefore, the life of the ball bearing increases 8 times when the load is reduced to half.
5. Practical Example:
- Suppose a ball bearing has a rated life of 10,000 hours under a given load condition.
- If the load is reduced to half, the new life of the bearing can be calculated using the L10 life equation.
- Assuming all other factors remain constant, the new life will be 8 times the original life, i.e., 8 x 10,000 = 80,000 hours.
In conclusion, reducing the load on a ball bearing to half results in a significant increase in its life. This is due to the relationship between load and life described by the L10 life equation, which shows that reducing the load by half increases the life of the bearing by 8 times.
Free Test
FREE
| Start Free Test |
Community Answer
If the load on a ball bearing is reduced to half, the life of the bal...
Given, Initially, w1 = w
Life = L1
After half of load, w2 =w/2
Life = L2
Considering the relation,
Lw3 = c
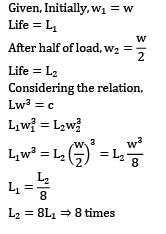
L2 = 8L1  times
times
 times
times

|
Explore Courses for Mechanical Engineering exam
|

|
Question Description
If the load on a ball bearing is reduced to half, the life of the ball bearing will be Ba) increases 8 timesb) increases 16 timesc) increases 2 timesd) increases 4 timesCorrect answer is option 'A'. Can you explain this answer? for Mechanical Engineering 2025 is part of Mechanical Engineering preparation. The Question and answers have been prepared according to the Mechanical Engineering exam syllabus. Information about If the load on a ball bearing is reduced to half, the life of the ball bearing will be Ba) increases 8 timesb) increases 16 timesc) increases 2 timesd) increases 4 timesCorrect answer is option 'A'. Can you explain this answer? covers all topics & solutions for Mechanical Engineering 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for If the load on a ball bearing is reduced to half, the life of the ball bearing will be Ba) increases 8 timesb) increases 16 timesc) increases 2 timesd) increases 4 timesCorrect answer is option 'A'. Can you explain this answer?.
If the load on a ball bearing is reduced to half, the life of the ball bearing will be Ba) increases 8 timesb) increases 16 timesc) increases 2 timesd) increases 4 timesCorrect answer is option 'A'. Can you explain this answer? for Mechanical Engineering 2025 is part of Mechanical Engineering preparation. The Question and answers have been prepared according to the Mechanical Engineering exam syllabus. Information about If the load on a ball bearing is reduced to half, the life of the ball bearing will be Ba) increases 8 timesb) increases 16 timesc) increases 2 timesd) increases 4 timesCorrect answer is option 'A'. Can you explain this answer? covers all topics & solutions for Mechanical Engineering 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for If the load on a ball bearing is reduced to half, the life of the ball bearing will be Ba) increases 8 timesb) increases 16 timesc) increases 2 timesd) increases 4 timesCorrect answer is option 'A'. Can you explain this answer?.
Solutions for If the load on a ball bearing is reduced to half, the life of the ball bearing will be Ba) increases 8 timesb) increases 16 timesc) increases 2 timesd) increases 4 timesCorrect answer is option 'A'. Can you explain this answer? in English & in Hindi are available as part of our courses for Mechanical Engineering.
Download more important topics, notes, lectures and mock test series for Mechanical Engineering Exam by signing up for free.
Here you can find the meaning of If the load on a ball bearing is reduced to half, the life of the ball bearing will be Ba) increases 8 timesb) increases 16 timesc) increases 2 timesd) increases 4 timesCorrect answer is option 'A'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
If the load on a ball bearing is reduced to half, the life of the ball bearing will be Ba) increases 8 timesb) increases 16 timesc) increases 2 timesd) increases 4 timesCorrect answer is option 'A'. Can you explain this answer?, a detailed solution for If the load on a ball bearing is reduced to half, the life of the ball bearing will be Ba) increases 8 timesb) increases 16 timesc) increases 2 timesd) increases 4 timesCorrect answer is option 'A'. Can you explain this answer? has been provided alongside types of If the load on a ball bearing is reduced to half, the life of the ball bearing will be Ba) increases 8 timesb) increases 16 timesc) increases 2 timesd) increases 4 timesCorrect answer is option 'A'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice If the load on a ball bearing is reduced to half, the life of the ball bearing will be Ba) increases 8 timesb) increases 16 timesc) increases 2 timesd) increases 4 timesCorrect answer is option 'A'. Can you explain this answer? tests, examples and also practice Mechanical Engineering tests.

|
Explore Courses for Mechanical Engineering exam
|

|
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.


















