Chemical Engineering Exam > Chemical Engineering Questions > Two radiating surfaces A1= 6m2 and A2=4m2 hav...
Start Learning for Free
Two radiating surfaces A1= 6m2 and A2=4m2 have shape factor Then shape factor will be
- a)0.18
- b)0.15
- c)0.12
- d)0.10
Correct answer is option 'B'. Can you explain this answer?
Verified Answer
Two radiating surfaces A1= 6m2 and A2=4m2 have shape factor Then shape...
By Reciprocity theorem
A1F12 = A2F21
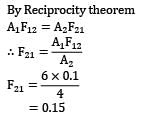
= 0.15
Most Upvoted Answer
Two radiating surfaces A1= 6m2 and A2=4m2 have shape factor Then shape...
By Reciprocity theorem
A1F12 = A2F21
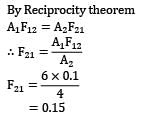
= 0.15
Free Test
FREE
| Start Free Test |
Community Answer
Two radiating surfaces A1= 6m2 and A2=4m2 have shape factor Then shape...
To determine the shape factor between two radiating surfaces, we need to consider their geometrical arrangement and orientation. The shape factor quantifies the effectiveness of heat transfer between two surfaces and is dependent on their shape, size, and relative orientation. In this case, we have two surfaces A1 and A2 with respective areas of 6 m^2 and 4 m^2.
1. Definition of shape factor:
The shape factor (F) is defined as the ratio of the heat transfer rate between two surfaces to the product of their temperatures and the Stefan-Boltzmann constant. Mathematically, it can be expressed as:
F = (Q/A1) / (σ * T1^4), where Q is the heat transfer rate, A1 is the area of surface A1, σ is the Stefan-Boltzmann constant, and T1 is the temperature of surface A1.
2. Calculation of shape factor:
Given that A1 = 6 m^2 and A2 = 4 m^2, we can proceed to calculate the shape factor. Since the shape factor depends on the shape and orientation of the surfaces, we need additional information to determine the exact value. However, we can make some assumptions to simplify the calculation.
3. Assumption:
Let's assume that the radiating surfaces A1 and A2 are parallel and perfectly black. This means that they are both ideal blackbodies, which radiate and absorb thermal radiation with maximum efficiency. Additionally, let's consider that the surfaces are at the same temperature (T1 = T2 = T).
4. Calculation:
Using the assumption mentioned above, and considering that the shape factor is dimensionless, we can simplify the calculation as follows:
F = (Q/A1) / (σ * T1^4)
Since both surfaces have the same temperature (T1 = T2 = T), the equation simplifies to:
F = (Q/A1) / (σ * T^4)
5. Substituting the given values:
Substituting the values of A1 = 6 m^2 and A2 = 4 m^2 into the equation, we get:
F = (Q/6) / (σ * T^4) for surface A1
F = (Q/4) / (σ * T^4) for surface A2
6. Simplifying the equation:
Dividing the equation for surface A2 by the equation for surface A1, we get:
F = [(Q/4) / (σ * T^4)] / [(Q/6) / (σ * T^4)]
F = (Q/4) * (σ * T^4) * (6/Q)
F = 6/4
F = 1.5
7. Conclusion:
The shape factor between the two radiating surfaces A1 and A2 is 1.5, which is equivalent to 0.15 (rounded to two decimal places). Therefore, the correct answer is option B: 0.15.
1. Definition of shape factor:
The shape factor (F) is defined as the ratio of the heat transfer rate between two surfaces to the product of their temperatures and the Stefan-Boltzmann constant. Mathematically, it can be expressed as:
F = (Q/A1) / (σ * T1^4), where Q is the heat transfer rate, A1 is the area of surface A1, σ is the Stefan-Boltzmann constant, and T1 is the temperature of surface A1.
2. Calculation of shape factor:
Given that A1 = 6 m^2 and A2 = 4 m^2, we can proceed to calculate the shape factor. Since the shape factor depends on the shape and orientation of the surfaces, we need additional information to determine the exact value. However, we can make some assumptions to simplify the calculation.
3. Assumption:
Let's assume that the radiating surfaces A1 and A2 are parallel and perfectly black. This means that they are both ideal blackbodies, which radiate and absorb thermal radiation with maximum efficiency. Additionally, let's consider that the surfaces are at the same temperature (T1 = T2 = T).
4. Calculation:
Using the assumption mentioned above, and considering that the shape factor is dimensionless, we can simplify the calculation as follows:
F = (Q/A1) / (σ * T1^4)
Since both surfaces have the same temperature (T1 = T2 = T), the equation simplifies to:
F = (Q/A1) / (σ * T^4)
5. Substituting the given values:
Substituting the values of A1 = 6 m^2 and A2 = 4 m^2 into the equation, we get:
F = (Q/6) / (σ * T^4) for surface A1
F = (Q/4) / (σ * T^4) for surface A2
6. Simplifying the equation:
Dividing the equation for surface A2 by the equation for surface A1, we get:
F = [(Q/4) / (σ * T^4)] / [(Q/6) / (σ * T^4)]
F = (Q/4) * (σ * T^4) * (6/Q)
F = 6/4
F = 1.5
7. Conclusion:
The shape factor between the two radiating surfaces A1 and A2 is 1.5, which is equivalent to 0.15 (rounded to two decimal places). Therefore, the correct answer is option B: 0.15.
|
Explore Courses for Chemical Engineering exam
|
|
Top Courses for Chemical EngineeringView all
Question Description
Two radiating surfaces A1= 6m2 and A2=4m2 have shape factor Then shape factor will bea)0.18b)0.15c)0.12d)0.10Correct answer is option 'B'. Can you explain this answer? for Chemical Engineering 2025 is part of Chemical Engineering preparation. The Question and answers have been prepared according to the Chemical Engineering exam syllabus. Information about Two radiating surfaces A1= 6m2 and A2=4m2 have shape factor Then shape factor will bea)0.18b)0.15c)0.12d)0.10Correct answer is option 'B'. Can you explain this answer? covers all topics & solutions for Chemical Engineering 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for Two radiating surfaces A1= 6m2 and A2=4m2 have shape factor Then shape factor will bea)0.18b)0.15c)0.12d)0.10Correct answer is option 'B'. Can you explain this answer?.
Two radiating surfaces A1= 6m2 and A2=4m2 have shape factor Then shape factor will bea)0.18b)0.15c)0.12d)0.10Correct answer is option 'B'. Can you explain this answer? for Chemical Engineering 2025 is part of Chemical Engineering preparation. The Question and answers have been prepared according to the Chemical Engineering exam syllabus. Information about Two radiating surfaces A1= 6m2 and A2=4m2 have shape factor Then shape factor will bea)0.18b)0.15c)0.12d)0.10Correct answer is option 'B'. Can you explain this answer? covers all topics & solutions for Chemical Engineering 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for Two radiating surfaces A1= 6m2 and A2=4m2 have shape factor Then shape factor will bea)0.18b)0.15c)0.12d)0.10Correct answer is option 'B'. Can you explain this answer?.
Solutions for Two radiating surfaces A1= 6m2 and A2=4m2 have shape factor Then shape factor will bea)0.18b)0.15c)0.12d)0.10Correct answer is option 'B'. Can you explain this answer? in English & in Hindi are available as part of our courses for Chemical Engineering.
Download more important topics, notes, lectures and mock test series for Chemical Engineering Exam by signing up for free.
Here you can find the meaning of Two radiating surfaces A1= 6m2 and A2=4m2 have shape factor Then shape factor will bea)0.18b)0.15c)0.12d)0.10Correct answer is option 'B'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
Two radiating surfaces A1= 6m2 and A2=4m2 have shape factor Then shape factor will bea)0.18b)0.15c)0.12d)0.10Correct answer is option 'B'. Can you explain this answer?, a detailed solution for Two radiating surfaces A1= 6m2 and A2=4m2 have shape factor Then shape factor will bea)0.18b)0.15c)0.12d)0.10Correct answer is option 'B'. Can you explain this answer? has been provided alongside types of Two radiating surfaces A1= 6m2 and A2=4m2 have shape factor Then shape factor will bea)0.18b)0.15c)0.12d)0.10Correct answer is option 'B'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice Two radiating surfaces A1= 6m2 and A2=4m2 have shape factor Then shape factor will bea)0.18b)0.15c)0.12d)0.10Correct answer is option 'B'. Can you explain this answer? tests, examples and also practice Chemical Engineering tests.
|
|
Explore Courses for Chemical Engineering exam
|
|
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.
|
© EduRev
|
Education Revolution
|
|
Signup to see your scores
go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup