Class 9 Exam > Class 9 Questions > Opposite angles of a Quadrilateral ABCD are e...
Start Learning for Free
Opposite angles of a Quadrilateral ABCD are equal. If AB = 4cm, find the length of CD.
- a)4cm
- b)3cm
- c)5cm
- d)2cm
Correct answer is option 'A'. Can you explain this answer?
Verified Answer
Opposite angles of a Quadrilateral ABCD are equal. If AB = 4cm, find t...
Consider ABCD as a quadrilateral
It is given that the opposite angles are equal hence the given quadrilateral is a parallelogram.
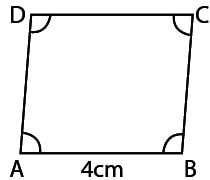

Here the opposite side of AB is CD
If AB = 4 cm then CD = 4 cm
Therefore, CD = 4 cm.
Most Upvoted Answer
Opposite angles of a Quadrilateral ABCD are equal. If AB = 4cm, find t...
In a quadrilateral whose opposite angles are equal then even even there opposite side will be equal, hence AB=CD so the option a is correct
Free Test
FREE
| Start Free Test |
Community Answer
Opposite angles of a Quadrilateral ABCD are equal. If AB = 4cm, find t...
To find the length of CD in the given quadrilateral ABCD, we can use the property that opposite angles of a quadrilateral are equal.
Given:
AB = 4 cm
Solution:
Let's label the opposite angles of the quadrilateral as ∠A and ∠C, and the sides opposite to these angles as AD and BC, respectively.
According to the property, ∠A = ∠C.
Now, we can use the property that the sum of angles in a quadrilateral is 360 degrees.
∠A + ∠B + ∠C + ∠D = 360°
Since ∠A = ∠C, we can rewrite the equation as:
∠A + ∠B + ∠A + ∠D = 360°
2∠A + ∠B + ∠D = 360°
But opposite angles are equal, so ∠A = ∠C = ∠B = ∠D
Substituting this into the equation:
2∠A + ∠A + ∠A = 360°
4∠A = 360°
∠A = 360° / 4
∠A = 90°
Now, we can use the property of a right-angled triangle to find the length of CD.
In triangle ABC, we have a right angle at B.
Using the Pythagorean theorem, we can find the length of BC:
BC² = AB² + AC²
BC² = 4² + AC²
BC² = 16 + AC²
Since opposite angles are equal, ∠A = ∠C = 90°.
In triangle ACD, we have a right angle at A.
Using the Pythagorean theorem, we can find the length of AC:
AC² = AD² + CD²
Since ∠A = ∠C = 90°, AD and CD are the legs of a right-angled triangle.
But AD = BC (opposite sides of a quadrilateral are equal), so we can substitute BC for AD in the equation:
AC² = BC² + CD²
AC² = 16 + CD²
Now, we know that AC = 4 cm and AC² = 16 + CD².
Substituting the values in the equation:
4² = 16 + CD²
16 = 16 + CD²
CD² = 16 - 16
CD² = 0
Taking the square root on both sides:
CD = √0
CD = 0
Therefore, the length of CD is 0 cm.
Since none of the given options match the calculated length, it appears that there may be an error in the question or options provided.
Given:
AB = 4 cm
Solution:
Let's label the opposite angles of the quadrilateral as ∠A and ∠C, and the sides opposite to these angles as AD and BC, respectively.
According to the property, ∠A = ∠C.
Now, we can use the property that the sum of angles in a quadrilateral is 360 degrees.
∠A + ∠B + ∠C + ∠D = 360°
Since ∠A = ∠C, we can rewrite the equation as:
∠A + ∠B + ∠A + ∠D = 360°
2∠A + ∠B + ∠D = 360°
But opposite angles are equal, so ∠A = ∠C = ∠B = ∠D
Substituting this into the equation:
2∠A + ∠A + ∠A = 360°
4∠A = 360°
∠A = 360° / 4
∠A = 90°
Now, we can use the property of a right-angled triangle to find the length of CD.
In triangle ABC, we have a right angle at B.
Using the Pythagorean theorem, we can find the length of BC:
BC² = AB² + AC²
BC² = 4² + AC²
BC² = 16 + AC²
Since opposite angles are equal, ∠A = ∠C = 90°.
In triangle ACD, we have a right angle at A.
Using the Pythagorean theorem, we can find the length of AC:
AC² = AD² + CD²
Since ∠A = ∠C = 90°, AD and CD are the legs of a right-angled triangle.
But AD = BC (opposite sides of a quadrilateral are equal), so we can substitute BC for AD in the equation:
AC² = BC² + CD²
AC² = 16 + CD²
Now, we know that AC = 4 cm and AC² = 16 + CD².
Substituting the values in the equation:
4² = 16 + CD²
16 = 16 + CD²
CD² = 16 - 16
CD² = 0
Taking the square root on both sides:
CD = √0
CD = 0
Therefore, the length of CD is 0 cm.
Since none of the given options match the calculated length, it appears that there may be an error in the question or options provided.

|
Explore Courses for Class 9 exam
|

|
Question Description
Opposite angles of a Quadrilateral ABCD are equal. If AB = 4cm, find the length of CD.a)4cmb)3cmc)5cmd)2cmCorrect answer is option 'A'. Can you explain this answer? for Class 9 2025 is part of Class 9 preparation. The Question and answers have been prepared according to the Class 9 exam syllabus. Information about Opposite angles of a Quadrilateral ABCD are equal. If AB = 4cm, find the length of CD.a)4cmb)3cmc)5cmd)2cmCorrect answer is option 'A'. Can you explain this answer? covers all topics & solutions for Class 9 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for Opposite angles of a Quadrilateral ABCD are equal. If AB = 4cm, find the length of CD.a)4cmb)3cmc)5cmd)2cmCorrect answer is option 'A'. Can you explain this answer?.
Opposite angles of a Quadrilateral ABCD are equal. If AB = 4cm, find the length of CD.a)4cmb)3cmc)5cmd)2cmCorrect answer is option 'A'. Can you explain this answer? for Class 9 2025 is part of Class 9 preparation. The Question and answers have been prepared according to the Class 9 exam syllabus. Information about Opposite angles of a Quadrilateral ABCD are equal. If AB = 4cm, find the length of CD.a)4cmb)3cmc)5cmd)2cmCorrect answer is option 'A'. Can you explain this answer? covers all topics & solutions for Class 9 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for Opposite angles of a Quadrilateral ABCD are equal. If AB = 4cm, find the length of CD.a)4cmb)3cmc)5cmd)2cmCorrect answer is option 'A'. Can you explain this answer?.
Solutions for Opposite angles of a Quadrilateral ABCD are equal. If AB = 4cm, find the length of CD.a)4cmb)3cmc)5cmd)2cmCorrect answer is option 'A'. Can you explain this answer? in English & in Hindi are available as part of our courses for Class 9.
Download more important topics, notes, lectures and mock test series for Class 9 Exam by signing up for free.
Here you can find the meaning of Opposite angles of a Quadrilateral ABCD are equal. If AB = 4cm, find the length of CD.a)4cmb)3cmc)5cmd)2cmCorrect answer is option 'A'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
Opposite angles of a Quadrilateral ABCD are equal. If AB = 4cm, find the length of CD.a)4cmb)3cmc)5cmd)2cmCorrect answer is option 'A'. Can you explain this answer?, a detailed solution for Opposite angles of a Quadrilateral ABCD are equal. If AB = 4cm, find the length of CD.a)4cmb)3cmc)5cmd)2cmCorrect answer is option 'A'. Can you explain this answer? has been provided alongside types of Opposite angles of a Quadrilateral ABCD are equal. If AB = 4cm, find the length of CD.a)4cmb)3cmc)5cmd)2cmCorrect answer is option 'A'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice Opposite angles of a Quadrilateral ABCD are equal. If AB = 4cm, find the length of CD.a)4cmb)3cmc)5cmd)2cmCorrect answer is option 'A'. Can you explain this answer? tests, examples and also practice Class 9 tests.

|
Explore Courses for Class 9 exam
|

|
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.


















