CAT Exam > CAT Questions > Directions for Questions: Answer the question...
Start Learning for Free
Directions for Questions: Answer the questions on the basis of information given below.
A farmer has 60 hens in his poultry farm. Each of these 60 hens lays one egg per day. On each day out of the eggs laid, some of the eggs are found to be rotten and some of the eggs get broken. Only the eggs that are neither rotten nor broken are taken to the market for sale but due to some unavoidable reasons some eggs are not sold. The eggs that are not sold are brought back to the poultry farm.
A farmer has 60 hens in his poultry farm. Each of these 60 hens lays one egg per day. On each day out of the eggs laid, some of the eggs are found to be rotten and some of the eggs get broken. Only the eggs that are neither rotten nor broken are taken to the market for sale but due to some unavoidable reasons some eggs are not sold. The eggs that are not sold are brought back to the poultry farm.
(2014)
Additional Information Given:
I. Out of the eggs that are brought back on each day, 40% are rotten and 20% are broken the next morning (and they are always integers).
II. Out of the eggs that are brought back to the poultry farm on each day, the eggs that are neither broken nor rotten are taken along with the eggs that are laid by the hens on the next day to the market for sale.
III. On any particular day the number of eggs that are not sold is less than 20% of the number of eggs that are taken to be sold out of the eggs that are laid on each day.
IV. Out of the eggs that are laid on each day, the number of eggs that are rotten is greater than 1 but less than 5 and the number of eggs that got broken is greater than 3 and less than 7.
V. Every week has five days and each week starts from day 1 and ends on day 5. Assume there are no eggs with the farmer at the beginning of day 1 of the given week.
Q. Find the minimum possible aggregate number of eggs sold on day 4 and day 5.
I. Out of the eggs that are brought back on each day, 40% are rotten and 20% are broken the next morning (and they are always integers).
II. Out of the eggs that are brought back to the poultry farm on each day, the eggs that are neither broken nor rotten are taken along with the eggs that are laid by the hens on the next day to the market for sale.
III. On any particular day the number of eggs that are not sold is less than 20% of the number of eggs that are taken to be sold out of the eggs that are laid on each day.
IV. Out of the eggs that are laid on each day, the number of eggs that are rotten is greater than 1 but less than 5 and the number of eggs that got broken is greater than 3 and less than 7.
V. Every week has five days and each week starts from day 1 and ends on day 5. Assume there are no eggs with the farmer at the beginning of day 1 of the given week.
Q. Find the minimum possible aggregate number of eggs sold on day 4 and day 5.
- a)84
- b)83
- c)86
- d)85
Correct answer is option 'C'. Can you explain this answer?
| FREE This question is part of | Download PDF Attempt this Test |
Verified Answer
Directions for Questions: Answer the questions on the basis of informa...
Number of eggs laid on each day = Number of hens in the poultry farm = 60.
Out of the eggs laid on each day, the number of eggs t h a t got rotten is either 2 or 3 or 4.
Out of the eggs laid on each day, the number of eggs that got broken is either 4 or 5 or 6.
Maximum possible number of eggs taken to the market for sale on day 1 = 60 – (2 + 4)
= 54.
Minimum possible number of eggs taken to the market for sale on day 1 = 60 – (4 + 6)
= 50.
The minimum number of eggs that are left unsold each day must be 5, as the number of eggs that are rotten and broken among them needs to be an integer. It can be at max 10, since number of egg left unsold on any day is lessthan 20% ofthe number of eggs laid on each day, i.e. 20% of 60 = 12.
So, the number of eggs that are sold on day 1 ranges from (50 – 10 = 40) to (54 – 5 = 49), (both inclusive).
On the next day again 60 eggs are laid, so from the above logic the range of number of eggs sold should again come out to be from 42 to 49 (both inclusive), but there are eggs that remain unsold at the end of the previous day.
Minimum possible number of eggs that are left over from the previous day and are taken along with the eggs laid on a day to the market for sale = 5 – (40% of 5) – (2% of 5) = 2.
Maximum possible number of eggsthat are left over from the previous day and are taken along with the eggs laid on a day to the market for sale = 10 – (40% of 10) – (20% of 10) = 4.
So, the range of number of eggs that are sold on day 2 varies from (40 + 2 = 42) to (49 + 4 = 53) (both inclusive) and this holds true for day 3, day 4 and day 5 also,

The minimum possible number of eggs that were sold on day 4 can be 42, 42 eggs are sold in the scenorio when 10 eggs are left unsold.
So, the next day i.e. day 5, the minimum number of eggs that were sold can be calculated as Out of the 60 eggs that were laid – maximum rotten and broken eggs can be removed which are 4 and 6 respectively. Thus, left with 50 eggs. Also, from the 10 eggs of the previous day maximum rotten and broken can be removed which are 4 and 2 respectively, thus left with 4 eggs only. So, out of the total 54 eggs, a maximum of only 10 eggs can be left unsold. Therefore, the minimum eggs thatwere sold on day 5 were 54 – 10 = 44.
Hence, aggregate sum of eggs is 42 + 44 = 86.
Note: Most of the students will make a mistake of considering 42 eggs for both the days but this is not possible on any two consecutive days simultaneously.
Out of the eggs laid on each day, the number of eggs t h a t got rotten is either 2 or 3 or 4.
Out of the eggs laid on each day, the number of eggs that got broken is either 4 or 5 or 6.
Maximum possible number of eggs taken to the market for sale on day 1 = 60 – (2 + 4)
= 54.
Minimum possible number of eggs taken to the market for sale on day 1 = 60 – (4 + 6)
= 50.
The minimum number of eggs that are left unsold each day must be 5, as the number of eggs that are rotten and broken among them needs to be an integer. It can be at max 10, since number of egg left unsold on any day is lessthan 20% ofthe number of eggs laid on each day, i.e. 20% of 60 = 12.
So, the number of eggs that are sold on day 1 ranges from (50 – 10 = 40) to (54 – 5 = 49), (both inclusive).
On the next day again 60 eggs are laid, so from the above logic the range of number of eggs sold should again come out to be from 42 to 49 (both inclusive), but there are eggs that remain unsold at the end of the previous day.
Minimum possible number of eggs that are left over from the previous day and are taken along with the eggs laid on a day to the market for sale = 5 – (40% of 5) – (2% of 5) = 2.
Maximum possible number of eggsthat are left over from the previous day and are taken along with the eggs laid on a day to the market for sale = 10 – (40% of 10) – (20% of 10) = 4.
So, the range of number of eggs that are sold on day 2 varies from (40 + 2 = 42) to (49 + 4 = 53) (both inclusive) and this holds true for day 3, day 4 and day 5 also,

The minimum possible number of eggs that were sold on day 4 can be 42, 42 eggs are sold in the scenorio when 10 eggs are left unsold.
So, the next day i.e. day 5, the minimum number of eggs that were sold can be calculated as Out of the 60 eggs that were laid – maximum rotten and broken eggs can be removed which are 4 and 6 respectively. Thus, left with 50 eggs. Also, from the 10 eggs of the previous day maximum rotten and broken can be removed which are 4 and 2 respectively, thus left with 4 eggs only. So, out of the total 54 eggs, a maximum of only 10 eggs can be left unsold. Therefore, the minimum eggs thatwere sold on day 5 were 54 – 10 = 44.
Hence, aggregate sum of eggs is 42 + 44 = 86.
Note: Most of the students will make a mistake of considering 42 eggs for both the days but this is not possible on any two consecutive days simultaneously.
Most Upvoted Answer
Directions for Questions: Answer the questions on the basis of informa...
Number of eggs laid on each day = Number of hens in the poultry farm = 60.
Out of the eggs laid on each day, the number of eggs t h a t got rotten is either 2 or 3 or 4.
Out of the eggs laid on each day, the number of eggs that got broken is either 4 or 5 or 6.
Maximum possible number of eggs taken to the market for sale on day 1 = 60 – (2 + 4)
= 54.
Minimum possible number of eggs taken to the market for sale on day 1 = 60 – (4 + 6)
= 50.
The minimum number of eggs that are left unsold each day must be 5, as the number of eggs that are rotten and broken among them needs to be an integer. It can be at max 10, since number of egg left unsold on any day is lessthan 20% ofthe number of eggs laid on each day, i.e. 20% of 60 = 12.
So, the number of eggs that are sold on day 1 ranges from (50 – 10 = 40) to (54 – 5 = 49), (both inclusive).
On the next day again 60 eggs are laid, so from the above logic the range of number of eggs sold should again come out to be from 42 to 49 (both inclusive), but there are eggs that remain unsold at the end of the previous day.
Minimum possible number of eggs that are left over from the previous day and are taken along with the eggs laid on a day to the market for sale = 5 – (40% of 5) – (2% of 5) = 2.
Maximum possible number of eggsthat are left over from the previous day and are taken along with the eggs laid on a day to the market for sale = 10 – (40% of 10) – (20% of 10) = 4.
So, the range of number of eggs that are sold on day 2 varies from (40 + 2 = 42) to (49 + 4 = 53) (both inclusive) and this holds true for day 3, day 4 and day 5 also,
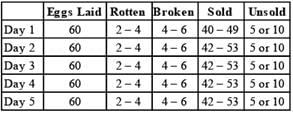
The minimum possible number of eggs that were sold on day 4 can be 42, 42 eggs are sold in the scenorio when 10 eggs are left unsold.
So, the next day i.e. day 5, the minimum number of eggs that were sold can be calculated as Out of the 60 eggs that were laid – maximum rotten and broken eggs can be removed which are 4 and 6 respectively. Thus, left with 50 eggs. Also, from the 10 eggs of the previous day maximum rotten and broken can be removed which are 4 and 2 respectively, thus left with 4 eggs only. So, out of the total 54 eggs, a maximum of only 10 eggs can be left unsold. Therefore, the minimum eggs thatwere sold on day 5 were 54 – 10 = 44.
Hence, aggregate sum of eggs is 42 + 44 = 86.
Note: Most of the students will make a mistake of considering 42 eggs for both the days but this is not possible on any two consecutive days simultaneously.
Out of the eggs laid on each day, the number of eggs t h a t got rotten is either 2 or 3 or 4.
Out of the eggs laid on each day, the number of eggs that got broken is either 4 or 5 or 6.
Maximum possible number of eggs taken to the market for sale on day 1 = 60 – (2 + 4)
= 54.
Minimum possible number of eggs taken to the market for sale on day 1 = 60 – (4 + 6)
= 50.
The minimum number of eggs that are left unsold each day must be 5, as the number of eggs that are rotten and broken among them needs to be an integer. It can be at max 10, since number of egg left unsold on any day is lessthan 20% ofthe number of eggs laid on each day, i.e. 20% of 60 = 12.
So, the number of eggs that are sold on day 1 ranges from (50 – 10 = 40) to (54 – 5 = 49), (both inclusive).
On the next day again 60 eggs are laid, so from the above logic the range of number of eggs sold should again come out to be from 42 to 49 (both inclusive), but there are eggs that remain unsold at the end of the previous day.
Minimum possible number of eggs that are left over from the previous day and are taken along with the eggs laid on a day to the market for sale = 5 – (40% of 5) – (2% of 5) = 2.
Maximum possible number of eggsthat are left over from the previous day and are taken along with the eggs laid on a day to the market for sale = 10 – (40% of 10) – (20% of 10) = 4.
So, the range of number of eggs that are sold on day 2 varies from (40 + 2 = 42) to (49 + 4 = 53) (both inclusive) and this holds true for day 3, day 4 and day 5 also,

The minimum possible number of eggs that were sold on day 4 can be 42, 42 eggs are sold in the scenorio when 10 eggs are left unsold.
So, the next day i.e. day 5, the minimum number of eggs that were sold can be calculated as Out of the 60 eggs that were laid – maximum rotten and broken eggs can be removed which are 4 and 6 respectively. Thus, left with 50 eggs. Also, from the 10 eggs of the previous day maximum rotten and broken can be removed which are 4 and 2 respectively, thus left with 4 eggs only. So, out of the total 54 eggs, a maximum of only 10 eggs can be left unsold. Therefore, the minimum eggs thatwere sold on day 5 were 54 – 10 = 44.
Hence, aggregate sum of eggs is 42 + 44 = 86.
Note: Most of the students will make a mistake of considering 42 eggs for both the days but this is not possible on any two consecutive days simultaneously.
Free Test
FREE
| Start Free Test |
Community Answer
Directions for Questions: Answer the questions on the basis of informa...
Number of eggs laid on each day = Number of hens in the poultry farm = 60.
Out of the eggs laid on each day, the number of eggs t h a t got rotten is either 2 or 3 or 4.
Out of the eggs laid on each day, the number of eggs that got broken is either 4 or 5 or 6.
Maximum possible number of eggs taken to the market for sale on day 1 = 60 – (2 + 4)
= 54.
Minimum possible number of eggs taken to the market for sale on day 1 = 60 – (4 + 6)
= 50.
The minimum number of eggs that are left unsold each day must be 5, as the number of eggs that are rotten and broken among them needs to be an integer. It can be at max 10, since number of egg left unsold on any day is lessthan 20% ofthe number of eggs laid on each day, i.e. 20% of 60 = 12.
So, the number of eggs that are sold on day 1 ranges from (50 – 10 = 40) to (54 – 5 = 49), (both inclusive).
On the next day again 60 eggs are laid, so from the above logic the range of number of eggs sold should again come out to be from 42 to 49 (both inclusive), but there are eggs that remain unsold at the end of the previous day.
Minimum possible number of eggs that are left over from the previous day and are taken along with the eggs laid on a day to the market for sale = 5 – (40% of 5) – (2% of 5) = 2.
Maximum possible number of eggsthat are left over from the previous day and are taken along with the eggs laid on a day to the market for sale = 10 – (40% of 10) – (20% of 10) = 4.
So, the range of number of eggs that are sold on day 2 varies from (40 + 2 = 42) to (49 + 4 = 53) (both inclusive) and this holds true for day 3, day 4 and day 5 also,

The minimum possible number of eggs that were sold on day 4 can be 42, 42 eggs are sold in the scenorio when 10 eggs are left unsold.
So, the next day i.e. day 5, the minimum number of eggs that were sold can be calculated as Out of the 60 eggs that were laid – maximum rotten and broken eggs can be removed which are 4 and 6 respectively. Thus, left with 50 eggs. Also, from the 10 eggs of the previous day maximum rotten and broken can be removed which are 4 and 2 respectively, thus left with 4 eggs only. So, out of the total 54 eggs, a maximum of only 10 eggs can be left unsold. Therefore, the minimum eggs thatwere sold on day 5 were 54 – 10 = 44.
Hence, aggregate sum of eggs is 42 + 44 = 86.
Note: Most of the students will make a mistake of considering 42 eggs for both the days but this is not possible on any two consecutive days simultaneously.
Out of the eggs laid on each day, the number of eggs t h a t got rotten is either 2 or 3 or 4.
Out of the eggs laid on each day, the number of eggs that got broken is either 4 or 5 or 6.
Maximum possible number of eggs taken to the market for sale on day 1 = 60 – (2 + 4)
= 54.
Minimum possible number of eggs taken to the market for sale on day 1 = 60 – (4 + 6)
= 50.
The minimum number of eggs that are left unsold each day must be 5, as the number of eggs that are rotten and broken among them needs to be an integer. It can be at max 10, since number of egg left unsold on any day is lessthan 20% ofthe number of eggs laid on each day, i.e. 20% of 60 = 12.
So, the number of eggs that are sold on day 1 ranges from (50 – 10 = 40) to (54 – 5 = 49), (both inclusive).
On the next day again 60 eggs are laid, so from the above logic the range of number of eggs sold should again come out to be from 42 to 49 (both inclusive), but there are eggs that remain unsold at the end of the previous day.
Minimum possible number of eggs that are left over from the previous day and are taken along with the eggs laid on a day to the market for sale = 5 – (40% of 5) – (2% of 5) = 2.
Maximum possible number of eggsthat are left over from the previous day and are taken along with the eggs laid on a day to the market for sale = 10 – (40% of 10) – (20% of 10) = 4.
So, the range of number of eggs that are sold on day 2 varies from (40 + 2 = 42) to (49 + 4 = 53) (both inclusive) and this holds true for day 3, day 4 and day 5 also,

The minimum possible number of eggs that were sold on day 4 can be 42, 42 eggs are sold in the scenorio when 10 eggs are left unsold.
So, the next day i.e. day 5, the minimum number of eggs that were sold can be calculated as Out of the 60 eggs that were laid – maximum rotten and broken eggs can be removed which are 4 and 6 respectively. Thus, left with 50 eggs. Also, from the 10 eggs of the previous day maximum rotten and broken can be removed which are 4 and 2 respectively, thus left with 4 eggs only. So, out of the total 54 eggs, a maximum of only 10 eggs can be left unsold. Therefore, the minimum eggs thatwere sold on day 5 were 54 – 10 = 44.
Hence, aggregate sum of eggs is 42 + 44 = 86.
Note: Most of the students will make a mistake of considering 42 eggs for both the days but this is not possible on any two consecutive days simultaneously.
Attention CAT Students!
To make sure you are not studying endlessly, EduRev has designed CAT study material, with Structured Courses, Videos, & Test Series. Plus get personalized analysis, doubt solving and improvement plans to achieve a great score in CAT.

|
Explore Courses for CAT exam
|

|
Similar CAT Doubts
Directions for Questions: Answer the questions on the basis of information given below.A farmer has 60 hens in his poultry farm. Each of these 60 hens lays one egg per day. On each day out of the eggs laid, some of the eggs are found to be rotten and some of the eggs get broken. Only the eggs that are neither rotten nor broken are taken to the market for sale but due to some unavoidable reasons some eggs are not sold. The eggs that are not sold are brought back to the poultry farm.(2014)Additional Information Given: I. Out of the eggs that are brought back on each day, 40% are rotten and 20% are broken the next morning (and they are always integers).II. Out of the eggs that are brought back to the poultry farm on each day, the eggs that are neither broken nor rotten are taken along with the eggs that are laid by the hens on the next day to the market for sale.III. On any particular day the number of eggs that are not sold is less than 20% of the number of eggs that are taken to be sold out of the eggs that are laid on each day.IV. Out of the eggs that are laid on each day, the number of eggs that are rotten is greater than 1 but less than 5 and the number of eggs that got broken is greater than 3 and less than 7.V. Every week has five days and each week starts from day 1 and ends on day 5. Assume there are no eggs with the farmer at the beginning of day 1 of the given week.Q.Find the minimum possible aggregate number of eggs sold on day 4 and day 5.a)84b)83c)86d)85Correct answer is option 'C'. Can you explain this answer?
Question Description
Directions for Questions: Answer the questions on the basis of information given below.A farmer has 60 hens in his poultry farm. Each of these 60 hens lays one egg per day. On each day out of the eggs laid, some of the eggs are found to be rotten and some of the eggs get broken. Only the eggs that are neither rotten nor broken are taken to the market for sale but due to some unavoidable reasons some eggs are not sold. The eggs that are not sold are brought back to the poultry farm.(2014)Additional Information Given: I. Out of the eggs that are brought back on each day, 40% are rotten and 20% are broken the next morning (and they are always integers).II. Out of the eggs that are brought back to the poultry farm on each day, the eggs that are neither broken nor rotten are taken along with the eggs that are laid by the hens on the next day to the market for sale.III. On any particular day the number of eggs that are not sold is less than 20% of the number of eggs that are taken to be sold out of the eggs that are laid on each day.IV. Out of the eggs that are laid on each day, the number of eggs that are rotten is greater than 1 but less than 5 and the number of eggs that got broken is greater than 3 and less than 7.V. Every week has five days and each week starts from day 1 and ends on day 5. Assume there are no eggs with the farmer at the beginning of day 1 of the given week.Q.Find the minimum possible aggregate number of eggs sold on day 4 and day 5.a)84b)83c)86d)85Correct answer is option 'C'. Can you explain this answer? for CAT 2024 is part of CAT preparation. The Question and answers have been prepared according to the CAT exam syllabus. Information about Directions for Questions: Answer the questions on the basis of information given below.A farmer has 60 hens in his poultry farm. Each of these 60 hens lays one egg per day. On each day out of the eggs laid, some of the eggs are found to be rotten and some of the eggs get broken. Only the eggs that are neither rotten nor broken are taken to the market for sale but due to some unavoidable reasons some eggs are not sold. The eggs that are not sold are brought back to the poultry farm.(2014)Additional Information Given: I. Out of the eggs that are brought back on each day, 40% are rotten and 20% are broken the next morning (and they are always integers).II. Out of the eggs that are brought back to the poultry farm on each day, the eggs that are neither broken nor rotten are taken along with the eggs that are laid by the hens on the next day to the market for sale.III. On any particular day the number of eggs that are not sold is less than 20% of the number of eggs that are taken to be sold out of the eggs that are laid on each day.IV. Out of the eggs that are laid on each day, the number of eggs that are rotten is greater than 1 but less than 5 and the number of eggs that got broken is greater than 3 and less than 7.V. Every week has five days and each week starts from day 1 and ends on day 5. Assume there are no eggs with the farmer at the beginning of day 1 of the given week.Q.Find the minimum possible aggregate number of eggs sold on day 4 and day 5.a)84b)83c)86d)85Correct answer is option 'C'. Can you explain this answer? covers all topics & solutions for CAT 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for Directions for Questions: Answer the questions on the basis of information given below.A farmer has 60 hens in his poultry farm. Each of these 60 hens lays one egg per day. On each day out of the eggs laid, some of the eggs are found to be rotten and some of the eggs get broken. Only the eggs that are neither rotten nor broken are taken to the market for sale but due to some unavoidable reasons some eggs are not sold. The eggs that are not sold are brought back to the poultry farm.(2014)Additional Information Given: I. Out of the eggs that are brought back on each day, 40% are rotten and 20% are broken the next morning (and they are always integers).II. Out of the eggs that are brought back to the poultry farm on each day, the eggs that are neither broken nor rotten are taken along with the eggs that are laid by the hens on the next day to the market for sale.III. On any particular day the number of eggs that are not sold is less than 20% of the number of eggs that are taken to be sold out of the eggs that are laid on each day.IV. Out of the eggs that are laid on each day, the number of eggs that are rotten is greater than 1 but less than 5 and the number of eggs that got broken is greater than 3 and less than 7.V. Every week has five days and each week starts from day 1 and ends on day 5. Assume there are no eggs with the farmer at the beginning of day 1 of the given week.Q.Find the minimum possible aggregate number of eggs sold on day 4 and day 5.a)84b)83c)86d)85Correct answer is option 'C'. Can you explain this answer?.
Directions for Questions: Answer the questions on the basis of information given below.A farmer has 60 hens in his poultry farm. Each of these 60 hens lays one egg per day. On each day out of the eggs laid, some of the eggs are found to be rotten and some of the eggs get broken. Only the eggs that are neither rotten nor broken are taken to the market for sale but due to some unavoidable reasons some eggs are not sold. The eggs that are not sold are brought back to the poultry farm.(2014)Additional Information Given: I. Out of the eggs that are brought back on each day, 40% are rotten and 20% are broken the next morning (and they are always integers).II. Out of the eggs that are brought back to the poultry farm on each day, the eggs that are neither broken nor rotten are taken along with the eggs that are laid by the hens on the next day to the market for sale.III. On any particular day the number of eggs that are not sold is less than 20% of the number of eggs that are taken to be sold out of the eggs that are laid on each day.IV. Out of the eggs that are laid on each day, the number of eggs that are rotten is greater than 1 but less than 5 and the number of eggs that got broken is greater than 3 and less than 7.V. Every week has five days and each week starts from day 1 and ends on day 5. Assume there are no eggs with the farmer at the beginning of day 1 of the given week.Q.Find the minimum possible aggregate number of eggs sold on day 4 and day 5.a)84b)83c)86d)85Correct answer is option 'C'. Can you explain this answer? for CAT 2024 is part of CAT preparation. The Question and answers have been prepared according to the CAT exam syllabus. Information about Directions for Questions: Answer the questions on the basis of information given below.A farmer has 60 hens in his poultry farm. Each of these 60 hens lays one egg per day. On each day out of the eggs laid, some of the eggs are found to be rotten and some of the eggs get broken. Only the eggs that are neither rotten nor broken are taken to the market for sale but due to some unavoidable reasons some eggs are not sold. The eggs that are not sold are brought back to the poultry farm.(2014)Additional Information Given: I. Out of the eggs that are brought back on each day, 40% are rotten and 20% are broken the next morning (and they are always integers).II. Out of the eggs that are brought back to the poultry farm on each day, the eggs that are neither broken nor rotten are taken along with the eggs that are laid by the hens on the next day to the market for sale.III. On any particular day the number of eggs that are not sold is less than 20% of the number of eggs that are taken to be sold out of the eggs that are laid on each day.IV. Out of the eggs that are laid on each day, the number of eggs that are rotten is greater than 1 but less than 5 and the number of eggs that got broken is greater than 3 and less than 7.V. Every week has five days and each week starts from day 1 and ends on day 5. Assume there are no eggs with the farmer at the beginning of day 1 of the given week.Q.Find the minimum possible aggregate number of eggs sold on day 4 and day 5.a)84b)83c)86d)85Correct answer is option 'C'. Can you explain this answer? covers all topics & solutions for CAT 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for Directions for Questions: Answer the questions on the basis of information given below.A farmer has 60 hens in his poultry farm. Each of these 60 hens lays one egg per day. On each day out of the eggs laid, some of the eggs are found to be rotten and some of the eggs get broken. Only the eggs that are neither rotten nor broken are taken to the market for sale but due to some unavoidable reasons some eggs are not sold. The eggs that are not sold are brought back to the poultry farm.(2014)Additional Information Given: I. Out of the eggs that are brought back on each day, 40% are rotten and 20% are broken the next morning (and they are always integers).II. Out of the eggs that are brought back to the poultry farm on each day, the eggs that are neither broken nor rotten are taken along with the eggs that are laid by the hens on the next day to the market for sale.III. On any particular day the number of eggs that are not sold is less than 20% of the number of eggs that are taken to be sold out of the eggs that are laid on each day.IV. Out of the eggs that are laid on each day, the number of eggs that are rotten is greater than 1 but less than 5 and the number of eggs that got broken is greater than 3 and less than 7.V. Every week has five days and each week starts from day 1 and ends on day 5. Assume there are no eggs with the farmer at the beginning of day 1 of the given week.Q.Find the minimum possible aggregate number of eggs sold on day 4 and day 5.a)84b)83c)86d)85Correct answer is option 'C'. Can you explain this answer?.
Solutions for Directions for Questions: Answer the questions on the basis of information given below.A farmer has 60 hens in his poultry farm. Each of these 60 hens lays one egg per day. On each day out of the eggs laid, some of the eggs are found to be rotten and some of the eggs get broken. Only the eggs that are neither rotten nor broken are taken to the market for sale but due to some unavoidable reasons some eggs are not sold. The eggs that are not sold are brought back to the poultry farm.(2014)Additional Information Given: I. Out of the eggs that are brought back on each day, 40% are rotten and 20% are broken the next morning (and they are always integers).II. Out of the eggs that are brought back to the poultry farm on each day, the eggs that are neither broken nor rotten are taken along with the eggs that are laid by the hens on the next day to the market for sale.III. On any particular day the number of eggs that are not sold is less than 20% of the number of eggs that are taken to be sold out of the eggs that are laid on each day.IV. Out of the eggs that are laid on each day, the number of eggs that are rotten is greater than 1 but less than 5 and the number of eggs that got broken is greater than 3 and less than 7.V. Every week has five days and each week starts from day 1 and ends on day 5. Assume there are no eggs with the farmer at the beginning of day 1 of the given week.Q.Find the minimum possible aggregate number of eggs sold on day 4 and day 5.a)84b)83c)86d)85Correct answer is option 'C'. Can you explain this answer? in English & in Hindi are available as part of our courses for CAT.
Download more important topics, notes, lectures and mock test series for CAT Exam by signing up for free.
Here you can find the meaning of Directions for Questions: Answer the questions on the basis of information given below.A farmer has 60 hens in his poultry farm. Each of these 60 hens lays one egg per day. On each day out of the eggs laid, some of the eggs are found to be rotten and some of the eggs get broken. Only the eggs that are neither rotten nor broken are taken to the market for sale but due to some unavoidable reasons some eggs are not sold. The eggs that are not sold are brought back to the poultry farm.(2014)Additional Information Given: I. Out of the eggs that are brought back on each day, 40% are rotten and 20% are broken the next morning (and they are always integers).II. Out of the eggs that are brought back to the poultry farm on each day, the eggs that are neither broken nor rotten are taken along with the eggs that are laid by the hens on the next day to the market for sale.III. On any particular day the number of eggs that are not sold is less than 20% of the number of eggs that are taken to be sold out of the eggs that are laid on each day.IV. Out of the eggs that are laid on each day, the number of eggs that are rotten is greater than 1 but less than 5 and the number of eggs that got broken is greater than 3 and less than 7.V. Every week has five days and each week starts from day 1 and ends on day 5. Assume there are no eggs with the farmer at the beginning of day 1 of the given week.Q.Find the minimum possible aggregate number of eggs sold on day 4 and day 5.a)84b)83c)86d)85Correct answer is option 'C'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
Directions for Questions: Answer the questions on the basis of information given below.A farmer has 60 hens in his poultry farm. Each of these 60 hens lays one egg per day. On each day out of the eggs laid, some of the eggs are found to be rotten and some of the eggs get broken. Only the eggs that are neither rotten nor broken are taken to the market for sale but due to some unavoidable reasons some eggs are not sold. The eggs that are not sold are brought back to the poultry farm.(2014)Additional Information Given: I. Out of the eggs that are brought back on each day, 40% are rotten and 20% are broken the next morning (and they are always integers).II. Out of the eggs that are brought back to the poultry farm on each day, the eggs that are neither broken nor rotten are taken along with the eggs that are laid by the hens on the next day to the market for sale.III. On any particular day the number of eggs that are not sold is less than 20% of the number of eggs that are taken to be sold out of the eggs that are laid on each day.IV. Out of the eggs that are laid on each day, the number of eggs that are rotten is greater than 1 but less than 5 and the number of eggs that got broken is greater than 3 and less than 7.V. Every week has five days and each week starts from day 1 and ends on day 5. Assume there are no eggs with the farmer at the beginning of day 1 of the given week.Q.Find the minimum possible aggregate number of eggs sold on day 4 and day 5.a)84b)83c)86d)85Correct answer is option 'C'. Can you explain this answer?, a detailed solution for Directions for Questions: Answer the questions on the basis of information given below.A farmer has 60 hens in his poultry farm. Each of these 60 hens lays one egg per day. On each day out of the eggs laid, some of the eggs are found to be rotten and some of the eggs get broken. Only the eggs that are neither rotten nor broken are taken to the market for sale but due to some unavoidable reasons some eggs are not sold. The eggs that are not sold are brought back to the poultry farm.(2014)Additional Information Given: I. Out of the eggs that are brought back on each day, 40% are rotten and 20% are broken the next morning (and they are always integers).II. Out of the eggs that are brought back to the poultry farm on each day, the eggs that are neither broken nor rotten are taken along with the eggs that are laid by the hens on the next day to the market for sale.III. On any particular day the number of eggs that are not sold is less than 20% of the number of eggs that are taken to be sold out of the eggs that are laid on each day.IV. Out of the eggs that are laid on each day, the number of eggs that are rotten is greater than 1 but less than 5 and the number of eggs that got broken is greater than 3 and less than 7.V. Every week has five days and each week starts from day 1 and ends on day 5. Assume there are no eggs with the farmer at the beginning of day 1 of the given week.Q.Find the minimum possible aggregate number of eggs sold on day 4 and day 5.a)84b)83c)86d)85Correct answer is option 'C'. Can you explain this answer? has been provided alongside types of Directions for Questions: Answer the questions on the basis of information given below.A farmer has 60 hens in his poultry farm. Each of these 60 hens lays one egg per day. On each day out of the eggs laid, some of the eggs are found to be rotten and some of the eggs get broken. Only the eggs that are neither rotten nor broken are taken to the market for sale but due to some unavoidable reasons some eggs are not sold. The eggs that are not sold are brought back to the poultry farm.(2014)Additional Information Given: I. Out of the eggs that are brought back on each day, 40% are rotten and 20% are broken the next morning (and they are always integers).II. Out of the eggs that are brought back to the poultry farm on each day, the eggs that are neither broken nor rotten are taken along with the eggs that are laid by the hens on the next day to the market for sale.III. On any particular day the number of eggs that are not sold is less than 20% of the number of eggs that are taken to be sold out of the eggs that are laid on each day.IV. Out of the eggs that are laid on each day, the number of eggs that are rotten is greater than 1 but less than 5 and the number of eggs that got broken is greater than 3 and less than 7.V. Every week has five days and each week starts from day 1 and ends on day 5. Assume there are no eggs with the farmer at the beginning of day 1 of the given week.Q.Find the minimum possible aggregate number of eggs sold on day 4 and day 5.a)84b)83c)86d)85Correct answer is option 'C'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice Directions for Questions: Answer the questions on the basis of information given below.A farmer has 60 hens in his poultry farm. Each of these 60 hens lays one egg per day. On each day out of the eggs laid, some of the eggs are found to be rotten and some of the eggs get broken. Only the eggs that are neither rotten nor broken are taken to the market for sale but due to some unavoidable reasons some eggs are not sold. The eggs that are not sold are brought back to the poultry farm.(2014)Additional Information Given: I. Out of the eggs that are brought back on each day, 40% are rotten and 20% are broken the next morning (and they are always integers).II. Out of the eggs that are brought back to the poultry farm on each day, the eggs that are neither broken nor rotten are taken along with the eggs that are laid by the hens on the next day to the market for sale.III. On any particular day the number of eggs that are not sold is less than 20% of the number of eggs that are taken to be sold out of the eggs that are laid on each day.IV. Out of the eggs that are laid on each day, the number of eggs that are rotten is greater than 1 but less than 5 and the number of eggs that got broken is greater than 3 and less than 7.V. Every week has five days and each week starts from day 1 and ends on day 5. Assume there are no eggs with the farmer at the beginning of day 1 of the given week.Q.Find the minimum possible aggregate number of eggs sold on day 4 and day 5.a)84b)83c)86d)85Correct answer is option 'C'. Can you explain this answer? tests, examples and also practice CAT tests.

|
Explore Courses for CAT exam
|

|
Suggested Free Tests
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.
























