CAT Exam > CAT Questions > Let ABC be a right-angled isosceles triangle ...
Start Learning for Free
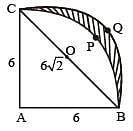
Let ABC be a right-angled isosceles triangle with hypotenuse BC. Let BQC be a semi-circle, away from A, with diameter BC. Let BPC be an arc of a circle centered at A and lying between BC and BQC. If AB has length 6 cm then the area, in sq cm, of the region enclosed by BPC and BQC is
(2017)
- a)9π – 18
- b)18π
- c)9π
- d)9
Correct answer is option 'B'. Can you explain this answer?
| FREE This question is part of | Download PDF Attempt this Test |
Verified Answer
Let ABC be a right-angled isosceles triangle with hypotenuse BC. Let B...
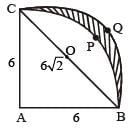
Enclosed Area = Area of semi circle BQC with centre O – Area of Arc BPC with O
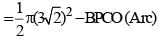 ...(i)
...(i)Now, Area of triangle ABC + BPCO (Arc) = Area of Quarter circle (ABPC)
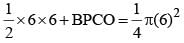
Area of BPCO = 9π –18
Put the value in equation (i)
Enclosed Area =
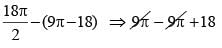 = 18 sq cm
= 18 sq cmMost Upvoted Answer
Let ABC be a right-angled isosceles triangle with hypotenuse BC. Let B...
Enclosed Area = Area of semi circle BQC with centre O – Area of Arc BPC with O
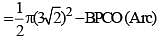 ...(i)
...(i)Now, Area of triangle ABC + BPCO (Arc) = Area of Quarter circle (ABPC)
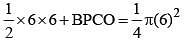
Area of BPCO = 9π –18
Put the value in equation (i)
Enclosed Area =
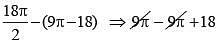 = 18 sq cm
= 18 sq cmAttention CAT Students!
To make sure you are not studying endlessly, EduRev has designed CAT study material, with Structured Courses, Videos, & Test Series. Plus get personalized analysis, doubt solving and improvement plans to achieve a great score in CAT.

|
Explore Courses for CAT exam
|

|
Let ABC be a right-angled isosceles triangle with hypotenuse BC. Let BQC be a semi-circle, away from A, with diameter BC. Let BPC be an arc of a circle centered at A and lying between BC and BQC. If AB has length 6 cm then the area, in sq cm, of the region enclosed by BPC and BQC is(2017)a)9π – 18b)18πc)9πd)9Correct answer is option 'B'. Can you explain this answer?
Question Description
Let ABC be a right-angled isosceles triangle with hypotenuse BC. Let BQC be a semi-circle, away from A, with diameter BC. Let BPC be an arc of a circle centered at A and lying between BC and BQC. If AB has length 6 cm then the area, in sq cm, of the region enclosed by BPC and BQC is(2017)a)9π – 18b)18πc)9πd)9Correct answer is option 'B'. Can you explain this answer? for CAT 2024 is part of CAT preparation. The Question and answers have been prepared according to the CAT exam syllabus. Information about Let ABC be a right-angled isosceles triangle with hypotenuse BC. Let BQC be a semi-circle, away from A, with diameter BC. Let BPC be an arc of a circle centered at A and lying between BC and BQC. If AB has length 6 cm then the area, in sq cm, of the region enclosed by BPC and BQC is(2017)a)9π – 18b)18πc)9πd)9Correct answer is option 'B'. Can you explain this answer? covers all topics & solutions for CAT 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for Let ABC be a right-angled isosceles triangle with hypotenuse BC. Let BQC be a semi-circle, away from A, with diameter BC. Let BPC be an arc of a circle centered at A and lying between BC and BQC. If AB has length 6 cm then the area, in sq cm, of the region enclosed by BPC and BQC is(2017)a)9π – 18b)18πc)9πd)9Correct answer is option 'B'. Can you explain this answer?.
Let ABC be a right-angled isosceles triangle with hypotenuse BC. Let BQC be a semi-circle, away from A, with diameter BC. Let BPC be an arc of a circle centered at A and lying between BC and BQC. If AB has length 6 cm then the area, in sq cm, of the region enclosed by BPC and BQC is(2017)a)9π – 18b)18πc)9πd)9Correct answer is option 'B'. Can you explain this answer? for CAT 2024 is part of CAT preparation. The Question and answers have been prepared according to the CAT exam syllabus. Information about Let ABC be a right-angled isosceles triangle with hypotenuse BC. Let BQC be a semi-circle, away from A, with diameter BC. Let BPC be an arc of a circle centered at A and lying between BC and BQC. If AB has length 6 cm then the area, in sq cm, of the region enclosed by BPC and BQC is(2017)a)9π – 18b)18πc)9πd)9Correct answer is option 'B'. Can you explain this answer? covers all topics & solutions for CAT 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for Let ABC be a right-angled isosceles triangle with hypotenuse BC. Let BQC be a semi-circle, away from A, with diameter BC. Let BPC be an arc of a circle centered at A and lying between BC and BQC. If AB has length 6 cm then the area, in sq cm, of the region enclosed by BPC and BQC is(2017)a)9π – 18b)18πc)9πd)9Correct answer is option 'B'. Can you explain this answer?.
Solutions for Let ABC be a right-angled isosceles triangle with hypotenuse BC. Let BQC be a semi-circle, away from A, with diameter BC. Let BPC be an arc of a circle centered at A and lying between BC and BQC. If AB has length 6 cm then the area, in sq cm, of the region enclosed by BPC and BQC is(2017)a)9π – 18b)18πc)9πd)9Correct answer is option 'B'. Can you explain this answer? in English & in Hindi are available as part of our courses for CAT.
Download more important topics, notes, lectures and mock test series for CAT Exam by signing up for free.
Here you can find the meaning of Let ABC be a right-angled isosceles triangle with hypotenuse BC. Let BQC be a semi-circle, away from A, with diameter BC. Let BPC be an arc of a circle centered at A and lying between BC and BQC. If AB has length 6 cm then the area, in sq cm, of the region enclosed by BPC and BQC is(2017)a)9π – 18b)18πc)9πd)9Correct answer is option 'B'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
Let ABC be a right-angled isosceles triangle with hypotenuse BC. Let BQC be a semi-circle, away from A, with diameter BC. Let BPC be an arc of a circle centered at A and lying between BC and BQC. If AB has length 6 cm then the area, in sq cm, of the region enclosed by BPC and BQC is(2017)a)9π – 18b)18πc)9πd)9Correct answer is option 'B'. Can you explain this answer?, a detailed solution for Let ABC be a right-angled isosceles triangle with hypotenuse BC. Let BQC be a semi-circle, away from A, with diameter BC. Let BPC be an arc of a circle centered at A and lying between BC and BQC. If AB has length 6 cm then the area, in sq cm, of the region enclosed by BPC and BQC is(2017)a)9π – 18b)18πc)9πd)9Correct answer is option 'B'. Can you explain this answer? has been provided alongside types of Let ABC be a right-angled isosceles triangle with hypotenuse BC. Let BQC be a semi-circle, away from A, with diameter BC. Let BPC be an arc of a circle centered at A and lying between BC and BQC. If AB has length 6 cm then the area, in sq cm, of the region enclosed by BPC and BQC is(2017)a)9π – 18b)18πc)9πd)9Correct answer is option 'B'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice Let ABC be a right-angled isosceles triangle with hypotenuse BC. Let BQC be a semi-circle, away from A, with diameter BC. Let BPC be an arc of a circle centered at A and lying between BC and BQC. If AB has length 6 cm then the area, in sq cm, of the region enclosed by BPC and BQC is(2017)a)9π – 18b)18πc)9πd)9Correct answer is option 'B'. Can you explain this answer? tests, examples and also practice CAT tests.

|
Explore Courses for CAT exam
|

|
Suggested Free Tests
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.






















