Mechanical Engineering Exam > Mechanical Engineering Questions > The velocity potential function for a source ...
Start Learning for Free
The velocity potential function for a source varies with the distance r as
[1987]
- a)1/r
- b)1/r2
- c)er
- d)In r
Correct answer is option 'D'. Can you explain this answer?
Verified Answer
The velocity potential function for a source varies with the distance ...
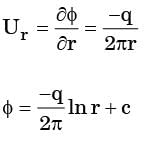
(2) 1 –d, 2 – d, 3 - c
(3) Closed contour in a flow field.
Most Upvoted Answer
The velocity potential function for a source varies with the distance ...
The velocity potential function for a source is a mathematical representation of the velocity field around a source. In fluid dynamics, a source refers to a point in space where fluid is being emitted or flowing outwards. The velocity potential function describes the velocity of the fluid at any point in space.
The velocity potential function for a source varies with the distance r. This means that as we move away from the source, the velocity potential changes. The given options are:
a) 1/r
b) 1/r^2
c) e^r
d) In r
The correct answer is option 'd' - In r.
Explanation:
To understand why the correct answer is 'In r', let's consider the nature of the velocity potential function for a source.
The velocity potential function for a source can be derived using potential flow theory. In potential flow, the fluid is assumed to be inviscid (no viscosity) and irrotational (no vorticity). This means that the fluid has no internal friction and there are no swirling motions.
For a source, the velocity potential function can be expressed as:
Φ = Q * ln(r)
Where:
Φ is the velocity potential function
Q is the strength of the source
ln(r) is the natural logarithm of the distance r from the source
From this equation, we can see that the velocity potential function is proportional to the natural logarithm of the distance. This is why the correct answer is 'In r'.
The natural logarithm function, ln(r), is commonly used to describe a wide range of phenomena in physics and mathematics. It has the property that it grows slowly as the argument (r in this case) increases. This makes it suitable for describing the decrease in velocity potential as we move away from the source.
In summary, the velocity potential function for a source varies with the distance r as In r. This means that the velocity potential decreases logarithmically as we move away from the source.
The velocity potential function for a source varies with the distance r. This means that as we move away from the source, the velocity potential changes. The given options are:
a) 1/r
b) 1/r^2
c) e^r
d) In r
The correct answer is option 'd' - In r.
Explanation:
To understand why the correct answer is 'In r', let's consider the nature of the velocity potential function for a source.
The velocity potential function for a source can be derived using potential flow theory. In potential flow, the fluid is assumed to be inviscid (no viscosity) and irrotational (no vorticity). This means that the fluid has no internal friction and there are no swirling motions.
For a source, the velocity potential function can be expressed as:
Φ = Q * ln(r)
Where:
Φ is the velocity potential function
Q is the strength of the source
ln(r) is the natural logarithm of the distance r from the source
From this equation, we can see that the velocity potential function is proportional to the natural logarithm of the distance. This is why the correct answer is 'In r'.
The natural logarithm function, ln(r), is commonly used to describe a wide range of phenomena in physics and mathematics. It has the property that it grows slowly as the argument (r in this case) increases. This makes it suitable for describing the decrease in velocity potential as we move away from the source.
In summary, the velocity potential function for a source varies with the distance r as In r. This means that the velocity potential decreases logarithmically as we move away from the source.

|
Explore Courses for Mechanical Engineering exam
|

|
Similar Mechanical Engineering Doubts
Question Description
The velocity potential function for a source varies with the distance r as[1987]a)1/rb)1/r2c)erd)In rCorrect answer is option 'D'. Can you explain this answer? for Mechanical Engineering 2025 is part of Mechanical Engineering preparation. The Question and answers have been prepared according to the Mechanical Engineering exam syllabus. Information about The velocity potential function for a source varies with the distance r as[1987]a)1/rb)1/r2c)erd)In rCorrect answer is option 'D'. Can you explain this answer? covers all topics & solutions for Mechanical Engineering 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for The velocity potential function for a source varies with the distance r as[1987]a)1/rb)1/r2c)erd)In rCorrect answer is option 'D'. Can you explain this answer?.
The velocity potential function for a source varies with the distance r as[1987]a)1/rb)1/r2c)erd)In rCorrect answer is option 'D'. Can you explain this answer? for Mechanical Engineering 2025 is part of Mechanical Engineering preparation. The Question and answers have been prepared according to the Mechanical Engineering exam syllabus. Information about The velocity potential function for a source varies with the distance r as[1987]a)1/rb)1/r2c)erd)In rCorrect answer is option 'D'. Can you explain this answer? covers all topics & solutions for Mechanical Engineering 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for The velocity potential function for a source varies with the distance r as[1987]a)1/rb)1/r2c)erd)In rCorrect answer is option 'D'. Can you explain this answer?.
Solutions for The velocity potential function for a source varies with the distance r as[1987]a)1/rb)1/r2c)erd)In rCorrect answer is option 'D'. Can you explain this answer? in English & in Hindi are available as part of our courses for Mechanical Engineering.
Download more important topics, notes, lectures and mock test series for Mechanical Engineering Exam by signing up for free.
Here you can find the meaning of The velocity potential function for a source varies with the distance r as[1987]a)1/rb)1/r2c)erd)In rCorrect answer is option 'D'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
The velocity potential function for a source varies with the distance r as[1987]a)1/rb)1/r2c)erd)In rCorrect answer is option 'D'. Can you explain this answer?, a detailed solution for The velocity potential function for a source varies with the distance r as[1987]a)1/rb)1/r2c)erd)In rCorrect answer is option 'D'. Can you explain this answer? has been provided alongside types of The velocity potential function for a source varies with the distance r as[1987]a)1/rb)1/r2c)erd)In rCorrect answer is option 'D'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice The velocity potential function for a source varies with the distance r as[1987]a)1/rb)1/r2c)erd)In rCorrect answer is option 'D'. Can you explain this answer? tests, examples and also practice Mechanical Engineering tests.

|
Explore Courses for Mechanical Engineering exam
|

|
Signup to solve all Doubts
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.























