Step-by-step solution
- Write the Laplace-domain relation for an inductor
For an inductor of inductance L with zero initial current:
V(s) = L s I(s) - Express I(s) in terms of the given voltage transform
Given V(s) = (4 s² + 3 s + 2) / (7 s² + 6 s + 5) and L = 2 H,
I(s) = V(s) / (L s)
= (4 s² + 3 s + 2) / [2 s (7 s² + 6 s + 5)] - Apply the Final-Value Theorem to find the steady current
The final-value theorem states that i(∞) = limₜ→∞ i(t) = limₛ→0 [s I(s)], provided all poles of s I(s) lie in the left half-plane.
So
i(∞) = limₛ→0 [s · (4 s² + 3 s + 2) / (2 s (7 s² + 6 s + 5))]
= limₛ→0 [(4 s² + 3 s + 2) / (2 (7 s² + 6 s + 5))]
= 2 / 10
= 0.2 A - Choose the correct option
The steady-state current is 0.2 A (Option B).
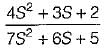 is applied across a 2H inductor having zero initial current What is the current in the inductor at t = ∞?
is applied across a 2H inductor having zero initial current What is the current in the inductor at t = ∞?
























