Railways Exam > Railways Questions > Moment of inertia about an axis perpendicular...
Start Learning for Free
Moment of inertia about an axis perpendicular to the plane of an area is known as
- a)First moment
- b)the Second moment
- c)Polar moment
- d)Axial moment
Correct answer is option 'C'. Can you explain this answer?
Verified Answer
Moment of inertia about an axis perpendicular to the plane of an area ...
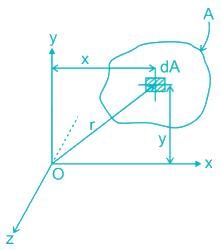
Polar moment of inertia:
The moment of inertia about an axis perpendicular to the plane of an area is known as the polar moment of inertia.
Let Oz be the axis perpendicular to the axis Ox and Oy passing through the origin O.
Moment of inertia of area of plane lamina about Oz axis is given by:
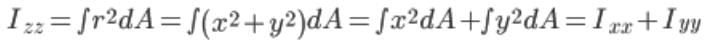
The moment of inertia of an area about an axis perpendicular to its plane (polar moment of inertia) at any point O is equal to the sum of moments of inertia about any two mutually perpendicular axis passing through the same point O and lying in the plane of area.
Most Upvoted Answer
Moment of inertia about an axis perpendicular to the plane of an area ...

Polar moment of inertia:
The moment of inertia about an axis perpendicular to the plane of an area is known as the polar moment of inertia.
Let Oz be the axis perpendicular to the axis Ox and Oy passing through the origin O.
Moment of inertia of area of plane lamina about Oz axis is given by:
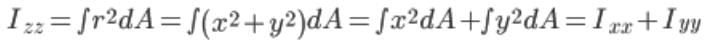
The moment of inertia of an area about an axis perpendicular to its plane (polar moment of inertia) at any point O is equal to the sum of moments of inertia about any two mutually perpendicular axis passing through the same point O and lying in the plane of area.
Free Test
FREE
| Start Free Test |
Community Answer
Moment of inertia about an axis perpendicular to the plane of an area ...
Understanding Moment of Inertia
The moment of inertia is a fundamental property in mechanics that quantifies how mass is distributed about an axis. In the context of an area, it’s crucial for analyzing how an object will respond to applied forces.
Types of Moments of Inertia
- First Moment: This relates to the distribution of area concerning an axis but does not consider the squared distance of the area elements. It’s often used in calculating centroids.
- Second Moment: This refers to the moment of inertia concerning an axis, but it is not specific to the perpendicular axis.
- Polar Moment: This is specifically the moment of inertia about an axis that is perpendicular to the plane of the area. It represents how the area resists torsion or twisting.
- Axial Moment: This term is often used interchangeably with the moment of inertia concerning an axis that is aligned with the object's length.
Why the Correct Answer is Polar Moment
The polar moment of inertia is particularly significant in structural and mechanical engineering. It helps in understanding torsional resistance and is calculated as the integral of the area times the square of the distance from the polar axis.
Key Points
- The polar moment of inertia is denoted as J.
- It plays a vital role in the design of shafts and other structural elements subjected to twisting forces.
- Understanding this property is essential for engineers and designers to ensure safety and performance in their structures.
In summary, the moment of inertia about an axis perpendicular to the area is known as the polar moment, making option 'C' the correct answer.
The moment of inertia is a fundamental property in mechanics that quantifies how mass is distributed about an axis. In the context of an area, it’s crucial for analyzing how an object will respond to applied forces.
Types of Moments of Inertia
- First Moment: This relates to the distribution of area concerning an axis but does not consider the squared distance of the area elements. It’s often used in calculating centroids.
- Second Moment: This refers to the moment of inertia concerning an axis, but it is not specific to the perpendicular axis.
- Polar Moment: This is specifically the moment of inertia about an axis that is perpendicular to the plane of the area. It represents how the area resists torsion or twisting.
- Axial Moment: This term is often used interchangeably with the moment of inertia concerning an axis that is aligned with the object's length.
Why the Correct Answer is Polar Moment
The polar moment of inertia is particularly significant in structural and mechanical engineering. It helps in understanding torsional resistance and is calculated as the integral of the area times the square of the distance from the polar axis.
Key Points
- The polar moment of inertia is denoted as J.
- It plays a vital role in the design of shafts and other structural elements subjected to twisting forces.
- Understanding this property is essential for engineers and designers to ensure safety and performance in their structures.
In summary, the moment of inertia about an axis perpendicular to the area is known as the polar moment, making option 'C' the correct answer.

|
Explore Courses for Railways exam
|

|
Question Description
Moment of inertia about an axis perpendicular to the plane of an area is known asa)First momentb)the Second momentc)Polar momentd)Axial momentCorrect answer is option 'C'. Can you explain this answer? for Railways 2025 is part of Railways preparation. The Question and answers have been prepared according to the Railways exam syllabus. Information about Moment of inertia about an axis perpendicular to the plane of an area is known asa)First momentb)the Second momentc)Polar momentd)Axial momentCorrect answer is option 'C'. Can you explain this answer? covers all topics & solutions for Railways 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for Moment of inertia about an axis perpendicular to the plane of an area is known asa)First momentb)the Second momentc)Polar momentd)Axial momentCorrect answer is option 'C'. Can you explain this answer?.
Moment of inertia about an axis perpendicular to the plane of an area is known asa)First momentb)the Second momentc)Polar momentd)Axial momentCorrect answer is option 'C'. Can you explain this answer? for Railways 2025 is part of Railways preparation. The Question and answers have been prepared according to the Railways exam syllabus. Information about Moment of inertia about an axis perpendicular to the plane of an area is known asa)First momentb)the Second momentc)Polar momentd)Axial momentCorrect answer is option 'C'. Can you explain this answer? covers all topics & solutions for Railways 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for Moment of inertia about an axis perpendicular to the plane of an area is known asa)First momentb)the Second momentc)Polar momentd)Axial momentCorrect answer is option 'C'. Can you explain this answer?.
Solutions for Moment of inertia about an axis perpendicular to the plane of an area is known asa)First momentb)the Second momentc)Polar momentd)Axial momentCorrect answer is option 'C'. Can you explain this answer? in English & in Hindi are available as part of our courses for Railways.
Download more important topics, notes, lectures and mock test series for Railways Exam by signing up for free.
Here you can find the meaning of Moment of inertia about an axis perpendicular to the plane of an area is known asa)First momentb)the Second momentc)Polar momentd)Axial momentCorrect answer is option 'C'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
Moment of inertia about an axis perpendicular to the plane of an area is known asa)First momentb)the Second momentc)Polar momentd)Axial momentCorrect answer is option 'C'. Can you explain this answer?, a detailed solution for Moment of inertia about an axis perpendicular to the plane of an area is known asa)First momentb)the Second momentc)Polar momentd)Axial momentCorrect answer is option 'C'. Can you explain this answer? has been provided alongside types of Moment of inertia about an axis perpendicular to the plane of an area is known asa)First momentb)the Second momentc)Polar momentd)Axial momentCorrect answer is option 'C'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice Moment of inertia about an axis perpendicular to the plane of an area is known asa)First momentb)the Second momentc)Polar momentd)Axial momentCorrect answer is option 'C'. Can you explain this answer? tests, examples and also practice Railways tests.

|
Explore Courses for Railways exam
|

|
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.























