CAT Exam > CAT Questions > The letters inside the circles given in the f...
Start Learning for Free
The letters inside the circles given in the figure below represent digits from 1 to 9, such that the sum of any three numbers which are connected in a straight line is equal.
It is also known that-
It is also known that-
- For any pair of two numbers, diametrically opposite to one another, the number represented by the alphabet which appears before the other one in the English dictionary is smaller than its pair.
- Each one of E and F does not represent 4.
- A, B and G are prime numbers and X is not a perfect square.
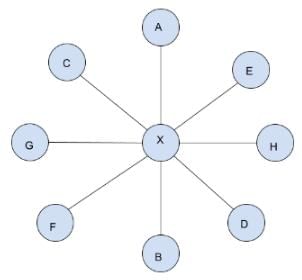
Q. What is the value of B?
- a)7
- b)5
- c)3
- d)Cannot be determined.
Correct answer is option 'A'. Can you explain this answer?
| FREE This question is part of | Download PDF Attempt this Test |
Verified Answer
The letters inside the circles given in the figure below represent dig...
It is given that each set of 3 numbers forming a straight line gives the same sum, let's say 'K'.
∵ A, B, C, D, E, F, G, H and X represents numbers from 1 to 9.
Sum of all the numbers
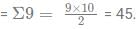
A+B+X = K .... (1)
C+D+X = K .... (2)
E+F+X = K .... (3)
G+H+X = K .... (4)
Adding all four above equations, we get:
A+B+C+D+E+F+G+H+X+3X= 4K
⇒ 45+ 3X= 4K
⇒ 3(15+X) = 4K.
∴ K should be a multiple of 3 and 4K should be greater than 45.
When K= 12, we have:
45 + 3X = 48
⇒ X= 1---- Case 1 (Not Possible because X is not a perfect square)
When K= 15, we have 45+3X= 60 and X= 5---- Case 2.
When K=18, we have 45+3X= 72 and X= 9----- Case 3 (Not possible because X is not a perfect square)
We can see from equations (1), (2), (3) and (4) that A+B= C+D= E+F= G+H
CASE 2 is the only possibility.
When sum= 15 and X=5.
A+B= C+D= E+F= G+H= 15-5= 10.
And hence any pair of diametrically opposite letters can represent pairs- (1,9), (2,8), (3,7) and (4,6)
Using the extra information given in the question, we can say that the pair that contains two prime numbers are (A,B)
∵ Only (3,7) forms such a pair, A=3 and B= 7 (A takes the lower number of the two because of the 1st point mentioned in the question).
Also, the only other prime number left is 2, which is taken up by G. If G=2, H=8
We are now left with pairs (E,F) and (C,D) which can take either (1,9) or (4,6).
∵ Neither E nor F is 4, E and F must represent 1 and 9 respectively and therefore C and D takes the values 4 and 6 respectively.
So, A= 3, B=7, C=4, D=6, E=1, F=9, G=2, H=8 and X=5.
∵ A, B, C, D, E, F, G, H and X represents numbers from 1 to 9.
Sum of all the numbers
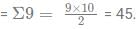
A+B+X = K .... (1)
C+D+X = K .... (2)
E+F+X = K .... (3)
G+H+X = K .... (4)
Adding all four above equations, we get:
A+B+C+D+E+F+G+H+X+3X= 4K
⇒ 45+ 3X= 4K
⇒ 3(15+X) = 4K.
∴ K should be a multiple of 3 and 4K should be greater than 45.
When K= 12, we have:
45 + 3X = 48
⇒ X= 1---- Case 1 (Not Possible because X is not a perfect square)
When K= 15, we have 45+3X= 60 and X= 5---- Case 2.
When K=18, we have 45+3X= 72 and X= 9----- Case 3 (Not possible because X is not a perfect square)
We can see from equations (1), (2), (3) and (4) that A+B= C+D= E+F= G+H
CASE 2 is the only possibility.
When sum= 15 and X=5.
A+B= C+D= E+F= G+H= 15-5= 10.
And hence any pair of diametrically opposite letters can represent pairs- (1,9), (2,8), (3,7) and (4,6)
Using the extra information given in the question, we can say that the pair that contains two prime numbers are (A,B)
∵ Only (3,7) forms such a pair, A=3 and B= 7 (A takes the lower number of the two because of the 1st point mentioned in the question).
Also, the only other prime number left is 2, which is taken up by G. If G=2, H=8
We are now left with pairs (E,F) and (C,D) which can take either (1,9) or (4,6).
∵ Neither E nor F is 4, E and F must represent 1 and 9 respectively and therefore C and D takes the values 4 and 6 respectively.
So, A= 3, B=7, C=4, D=6, E=1, F=9, G=2, H=8 and X=5.

|
Explore Courses for CAT exam
|

|
Similar CAT Doubts
The letters inside the circles given in the figure below represent digits from 1 to 9, such that the sum of any three numbers which are connected in a straight line is equal.It is also known that- For any pair of two numbers, diametrically opposite to one another, the number represented by the alphabet which appears before the other one in the English dictionary is smaller than its pair. Each one of E and F does not represent 4. A, B and G are prime numbers and X is not a perfect square. Q.What is the value of B?a)7b)5c)3d)Cannot be determined.Correct answer is option 'A'. Can you explain this answer?
Question Description
The letters inside the circles given in the figure below represent digits from 1 to 9, such that the sum of any three numbers which are connected in a straight line is equal.It is also known that- For any pair of two numbers, diametrically opposite to one another, the number represented by the alphabet which appears before the other one in the English dictionary is smaller than its pair. Each one of E and F does not represent 4. A, B and G are prime numbers and X is not a perfect square. Q.What is the value of B?a)7b)5c)3d)Cannot be determined.Correct answer is option 'A'. Can you explain this answer? for CAT 2024 is part of CAT preparation. The Question and answers have been prepared according to the CAT exam syllabus. Information about The letters inside the circles given in the figure below represent digits from 1 to 9, such that the sum of any three numbers which are connected in a straight line is equal.It is also known that- For any pair of two numbers, diametrically opposite to one another, the number represented by the alphabet which appears before the other one in the English dictionary is smaller than its pair. Each one of E and F does not represent 4. A, B and G are prime numbers and X is not a perfect square. Q.What is the value of B?a)7b)5c)3d)Cannot be determined.Correct answer is option 'A'. Can you explain this answer? covers all topics & solutions for CAT 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for The letters inside the circles given in the figure below represent digits from 1 to 9, such that the sum of any three numbers which are connected in a straight line is equal.It is also known that- For any pair of two numbers, diametrically opposite to one another, the number represented by the alphabet which appears before the other one in the English dictionary is smaller than its pair. Each one of E and F does not represent 4. A, B and G are prime numbers and X is not a perfect square. Q.What is the value of B?a)7b)5c)3d)Cannot be determined.Correct answer is option 'A'. Can you explain this answer?.
The letters inside the circles given in the figure below represent digits from 1 to 9, such that the sum of any three numbers which are connected in a straight line is equal.It is also known that- For any pair of two numbers, diametrically opposite to one another, the number represented by the alphabet which appears before the other one in the English dictionary is smaller than its pair. Each one of E and F does not represent 4. A, B and G are prime numbers and X is not a perfect square. Q.What is the value of B?a)7b)5c)3d)Cannot be determined.Correct answer is option 'A'. Can you explain this answer? for CAT 2024 is part of CAT preparation. The Question and answers have been prepared according to the CAT exam syllabus. Information about The letters inside the circles given in the figure below represent digits from 1 to 9, such that the sum of any three numbers which are connected in a straight line is equal.It is also known that- For any pair of two numbers, diametrically opposite to one another, the number represented by the alphabet which appears before the other one in the English dictionary is smaller than its pair. Each one of E and F does not represent 4. A, B and G are prime numbers and X is not a perfect square. Q.What is the value of B?a)7b)5c)3d)Cannot be determined.Correct answer is option 'A'. Can you explain this answer? covers all topics & solutions for CAT 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for The letters inside the circles given in the figure below represent digits from 1 to 9, such that the sum of any three numbers which are connected in a straight line is equal.It is also known that- For any pair of two numbers, diametrically opposite to one another, the number represented by the alphabet which appears before the other one in the English dictionary is smaller than its pair. Each one of E and F does not represent 4. A, B and G are prime numbers and X is not a perfect square. Q.What is the value of B?a)7b)5c)3d)Cannot be determined.Correct answer is option 'A'. Can you explain this answer?.
Solutions for The letters inside the circles given in the figure below represent digits from 1 to 9, such that the sum of any three numbers which are connected in a straight line is equal.It is also known that- For any pair of two numbers, diametrically opposite to one another, the number represented by the alphabet which appears before the other one in the English dictionary is smaller than its pair. Each one of E and F does not represent 4. A, B and G are prime numbers and X is not a perfect square. Q.What is the value of B?a)7b)5c)3d)Cannot be determined.Correct answer is option 'A'. Can you explain this answer? in English & in Hindi are available as part of our courses for CAT.
Download more important topics, notes, lectures and mock test series for CAT Exam by signing up for free.
Here you can find the meaning of The letters inside the circles given in the figure below represent digits from 1 to 9, such that the sum of any three numbers which are connected in a straight line is equal.It is also known that- For any pair of two numbers, diametrically opposite to one another, the number represented by the alphabet which appears before the other one in the English dictionary is smaller than its pair. Each one of E and F does not represent 4. A, B and G are prime numbers and X is not a perfect square. Q.What is the value of B?a)7b)5c)3d)Cannot be determined.Correct answer is option 'A'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
The letters inside the circles given in the figure below represent digits from 1 to 9, such that the sum of any three numbers which are connected in a straight line is equal.It is also known that- For any pair of two numbers, diametrically opposite to one another, the number represented by the alphabet which appears before the other one in the English dictionary is smaller than its pair. Each one of E and F does not represent 4. A, B and G are prime numbers and X is not a perfect square. Q.What is the value of B?a)7b)5c)3d)Cannot be determined.Correct answer is option 'A'. Can you explain this answer?, a detailed solution for The letters inside the circles given in the figure below represent digits from 1 to 9, such that the sum of any three numbers which are connected in a straight line is equal.It is also known that- For any pair of two numbers, diametrically opposite to one another, the number represented by the alphabet which appears before the other one in the English dictionary is smaller than its pair. Each one of E and F does not represent 4. A, B and G are prime numbers and X is not a perfect square. Q.What is the value of B?a)7b)5c)3d)Cannot be determined.Correct answer is option 'A'. Can you explain this answer? has been provided alongside types of The letters inside the circles given in the figure below represent digits from 1 to 9, such that the sum of any three numbers which are connected in a straight line is equal.It is also known that- For any pair of two numbers, diametrically opposite to one another, the number represented by the alphabet which appears before the other one in the English dictionary is smaller than its pair. Each one of E and F does not represent 4. A, B and G are prime numbers and X is not a perfect square. Q.What is the value of B?a)7b)5c)3d)Cannot be determined.Correct answer is option 'A'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice The letters inside the circles given in the figure below represent digits from 1 to 9, such that the sum of any three numbers which are connected in a straight line is equal.It is also known that- For any pair of two numbers, diametrically opposite to one another, the number represented by the alphabet which appears before the other one in the English dictionary is smaller than its pair. Each one of E and F does not represent 4. A, B and G are prime numbers and X is not a perfect square. Q.What is the value of B?a)7b)5c)3d)Cannot be determined.Correct answer is option 'A'. Can you explain this answer? tests, examples and also practice CAT tests.

|
Explore Courses for CAT exam
|

|
Suggested Free Tests
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.























