All Courses
Explore Courses UPSC Exam UPSC Test Series Free Notes EduRev Infinity Get the App Login Join for Free
Sign in Open App
CAT Exam  >  CAT Questions  >  Radheshyam is an alcohol bootlegger. He wants... Start Learning for Free
SaveJoin the Discussion on the App
Radheshyam is an alcohol bootlegger. He wants to make an extra profit on the alcohol, hence he tried to dilute the alcohol. He does this in a unique way. He takes 625 Liters of alcohol in a tank that has a large capacity. He replaces 20% of the content with water. After this, he doubles the quantity of alcohol in the tank by adding pure alcohol and then doubles the percentage of water in the mixture by adding pure water. 
His manager found this process tiresome and confusing. Therefore he suggested Radheshyamto mix the original 625L alcohol with a solution B of alcohol and water so that the resulting solution is the same as that derived from his initial process. What is the overall quantity and concentration of the suggested mixture B?
  • a)
    675.81L with 63.63% alcohol
  • b)
    675.81L with 71.42% alcohol
  • c)
    660.71L with 56.75% alcohol
  • d)
    785.71L  with 71.42% alcohol
Correct answer is option 'C'. Can you explain this answer?
FREE This question is part of
Download PDF Attempt Test
Download PDF Attempt this Test
Verified Answer
Radheshyam is an alcohol bootlegger. He wants to make an extra profit ...
Initially, Radheshyam had 625 litres of alcohol. After replacing 20% with water he has 125 Liters of water and 500 Liters of alcohol.
After doubling the alcohol content in the tank, he has 1000Liters of Alcohol and 125 Liters of water.
After this, he doubles the percentage of water in the solution by adding pure water. Let the amount of water be xx liters
As per the question
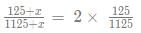
Upon rearranging and solving we get (125+x) 1125 = 250 (1125 + x)
875x = 125 x 125
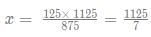
Therefore the final solution has 1000L of alcohol and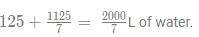 
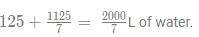
The added mixture should have 375L of alcohol and 2000/7 of water
Total quantity of mixture =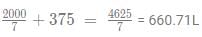 
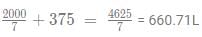
%concentration of alcohol = 
View all questions of this test
Most Upvoted Answer
Radheshyam is an alcohol bootlegger. He wants to make an extra profit ...
Given Information:
- Radheshyam starts with 625 liters of alcohol in a tank.
- He replaces 20% of the content with water.
- He then doubles the quantity of alcohol in the tank by adding pure alcohol.
- Finally, he doubles the percentage of water in the mixture by adding pure water.

Calculating the initial water content:
- Radheshyam replaces 20% of the 625 liters of alcohol with water, which means he adds 0.2 * 625 = 125 liters of water to the tank.
- Therefore, the initial water content in the tank is 125 liters.

Calculating the initial alcohol content:
- The remaining content in the tank after adding water is 625 - 125 = 500 liters.
- Radheshyam then doubles the quantity of alcohol in the tank by adding pure alcohol.
- This means he adds another 500 liters of pure alcohol to the tank.
- Therefore, the initial alcohol content in the tank is 500 + 500 = 1000 liters.

Calculating the final water content:
- Radheshyam doubles the percentage of water in the mixture by adding pure water.
- The initial water content was 125 liters, which is 20% of the total content.
- Doubling the percentage of water means it becomes 2 * 20% = 40% of the total content.
- Let's assume the final water content is x liters.
- Therefore, x liters is 40% of the total content, which is 1000 + x liters.
- We can write this as an equation: x = 0.4 * (1000 + x).
- Solving this equation, we get x = 400 liters.

Calculating the final alcohol content:
- The final alcohol content is the total content minus the final water content.
- Total content = initial water content + initial alcohol content = 125 + 1000 = 1125 liters.
- Final alcohol content = 1125 - 400 = 725 liters.

Calculating the overall quantity and concentration of the suggested mixture B:
- The suggested mixture B should have the same resulting solution as Radheshyam's initial process.
- The overall quantity of mixture B is the same as the original alcohol content, which is 1000 liters.
- The concentration of alcohol in the mixture B can be calculated as the percentage of alcohol in the final alcohol content.
- Concentration of alcohol in mixture B = (725 / 1000) * 100% = 72.5%.
- Therefore, the overall quantity and concentration of the suggested mixture B is 1000 liters with 72.5% alcohol.
- This corresponds to option (d) 785.71L with 71.42% alcohol.
- However, option (c) 660.71L with 56.75% alcohol is not the correct answer.
Attention CAT Students!
To make sure you are not studying endlessly, EduRev has designed CAT study material, with Structured Courses, Videos, & Test Series. Plus get personalized analysis, doubt solving and improvement plans to achieve a great score in CAT.
< Previous Question Next Question >
Explore Courses for CAT exam

Similar CAT Doubts

Direction: Read the following passage and answer the question that follows:There are several key difficulties surrounding the topic of percentages. Research has shown that there has been one difficulty which is more common than others; the meaning of the terms ‘of’ and ‘out of’. Hansen (2011) states that both terms represent an operator which needs explaining. Teachers need to address these before the topic is introduced to stop any confusion. ‘Of’ represents the multiplication operator, for example: 60% of 70 means 0.6 multiplied by 70; ‘out of’ represents the division operator, for example 30 out of 50 means 30 divided by 50. The teaching of these terms needs to be clear prior to teaching, so that children are confident in what these terms represent.Killen and Hindhaugh (2018) believe that once children understand that 1/10 is equal to 10% they will be able to use their knowledge of fractions to determine other multiples of 10. For example; Find 40% of 200. If children are aware that 10% is 20, then it will become obvious to them that 40% must be 80. This method enlightens many other practical ways to find other percentages of a quantity. Once children know 10%, they may also start finding half percent’s, such as; 5% or 25%. However, Killen and Hindhaugh (2018) state that a difficulty could occur when they are asking for a percentage of a quantity. If children are being asked to find the percentage, they may believe that the answer is always in percent. For example; find 60% of £480. Children may be capable of calculating the answer of 288 but instead of writing down £288, they may write down 288%. Teachers will need to explain this issue and address to children that once calculating the answer, it must be in the same units as the given quantity.Hansen also comments that the key to succession in the understanding of percentages is the relationship and understanding the children have with fractions and decimals. For example: they should be aware that 50% is equivalent to ½ and 0.5, and 25% is equivalent to ¼ and 0.25. Teaching these topics in isolation of each other should be strictly avoided as this may destroy a child’s deep mathematical understanding. Killen and Hindhaugh agree with this as they noted that children need to continually link decimals, fractions and percentages to their knowledge of the number system and operations that they are familiar with. Reys, et al (2010) believes however that percentages are more closely linked with ratios and proportions in mathematics and how important it is for teachers to teach these other topics to a high level. This is to later reduce the amount of errors a child has over percentages. However, these theorists also agree that understanding percentages requires no more new skills or concepts beyond those used in identifying fractions, decimals, ratios and proportions. Reys, et al states that an effective way of starting these topics is to explore children’s basic knowledge of what percentage means to them.Barmby et al noted that a misconception occurs whenever a learner’s outlook of a task does not connect to the accepted meaning of the overall concept. Ryan and Williams state that it is more damaging for children to have misconceptions of mathematical concepts than difficulties calculating them. Killen and Hindhaugh begin to talk how the use of rules and recipes are commonly used more so by teachers that are not fully confident with percentages. The main point of the argument is that if children are taught these rules linked to percentages, misconceptions can occur. This could be caused if the child forgets or misapplies the rule to their working out.This method is not the most reliable for children but can be a quick alternative for teachers to teach their class, if they are not fully confident in the topic themselves. This links to one of the most common misconceptions in the primary classroom. Killen and Hindhaugh state that it is the teacher’s responsibility for their children’s successes in that subject area. If the teaching is effective, then the child will become more confident and develop more links revolving around the topic of percentages. This will result in the child having a high level of understanding. However, if the teaching is not up to standard the child may lose confidence in themselves and end up being confused with the simplest of questions.Q. Which of the following statements best describes the relationship between percentages, fractions, decimals, ratios, and proportions according to the passage?

Direction: Read the following passage and answer the question that follows:There are several key difficulties surrounding the topic of percentages. Research has shown that there has been one difficulty which is more common than others; the meaning of the terms ‘of’ and ‘out of’. Hansen (2011) states that both terms represent an operator which needs explaining. Teachers need to address these before the topic is introduced to stop any confusion. ‘Of’ represents the multiplication operator, for example: 60% of 70 means 0.6 multiplied by 70; ‘out of’ represents the division operator, for example 30 out of 50 means 30 divided by 50. The teaching of these terms needs to be clear prior to teaching, so that children are confident in what these terms represent.Killen and Hindhaugh (2018) believe that once children understand that 1/10 is equal to 10% they will be able to use their knowledge of fractions to determine other multiples of 10. For example; Find 40% of 200. If children are aware that 10% is 20, then it will become obvious to them that 40% must be 80. This method enlightens many other practical ways to find other percentages of a quantity. Once children know 10%, they may also start finding half percent’s, such as; 5% or 25%. However, Killen and Hindhaugh (2018) state that a difficulty could occur when they are asking for a percentage of a quantity. If children are being asked to find the percentage, they may believe that the answer is always in percent. For example; find 60% of £480. Children may be capable of calculating the answer of 288 but instead of writing down £288, they may write down 288%. Teachers will need to explain this issue and address to children that once calculating the answer, it must be in the same units as the given quantity.Hansen also comments that the key to succession in the understanding of percentages is the relationship and understanding the children have with fractions and decimals. For example: they should be aware that 50% is equivalent to ½ and 0.5, and 25% is equivalent to ¼ and 0.25. Teaching these topics in isolation of each other should be strictly avoided as this may destroy a child’s deep mathematical understanding. Killen and Hindhaugh agree with this as they noted that children need to continually link decimals, fractions and percentages to their knowledge of the number system and operations that they are familiar with. Reys, et al (2010) believes however that percentages are more closely linked with ratios and proportions in mathematics and how important it is for teachers to teach these other topics to a high level. This is to later reduce the amount of errors a child has over percentages. However, these theorists also agree that understanding percentages requires no more new skills or concepts beyond those used in identifying fractions, decimals, ratios and proportions. Reys, et al states that an effective way of starting these topics is to explore children’s basic knowledge of what percentage means to them.Barmby et al noted that a misconception occurs whenever a learner’s outlook of a task does not connect to the accepted meaning of the overall concept. Ryan and Williams state that it is more damaging for children to have misconceptions of mathematical concepts than difficulties calculating them. Killen and Hindhaugh begin to talk how the use of rules and recipes are commonly used more so by teachers that are not fully confident with percentages. The main point of the argument is that if children are taught these rules linked to percentages, misconceptions can occur. This could be caused if the child forgets or misapplies the rule to their working out.This method is not the most reliable for children but can be a quick alternative for teachers to teach their class, if they are not fully confident in the topic themselves. This links to one of the most common misconceptions in the primary classroom. Killen and Hindhaugh state that it is the teacher’s responsibility for their children’s successes in that subject area. If the teaching is effective, then the child will become more confident and develop more links revolving around the topic of percentages. This will result in the child having a high level of understanding. However, if the teaching is not up to standard the child may lose confidence in themselves and end up being confused with the simplest of questions.Q. It can be inferred from the passage that the author is not likely to support the view that

Direction: Read the following passage and answer the question that follows:There are several key difficulties surrounding the topic of percentages. Research has shown that there has been one difficulty which is more common than others; the meaning of the terms ‘of’ and ‘out of’. Hansen (2011) states that both terms represent an operator which needs explaining. Teachers need to address these before the topic is introduced to stop any confusion. ‘Of’ represents the multiplication operator, for example: 60% of 70 means 0.6 multiplied by 70; ‘out of’ represents the division operator, for example 30 out of 50 means 30 divided by 50. The teaching of these terms needs to be clear prior to teaching, so that children are confident in what these terms represent.Killen and Hindhaugh (2018) believe that once children understand that 1/10 is equal to 10% they will be able to use their knowledge of fractions to determine other multiples of 10. For example; Find 40% of 200. If children are aware that 10% is 20, then it will become obvious to them that 40% must be 80. This method enlightens many other practical ways to find other percentages of a quantity. Once children know 10%, they may also start finding half percent’s, such as; 5% or 25%. However, Killen and Hindhaugh (2018) state that a difficulty could occur when they are asking for a percentage of a quantity. If children are being asked to find the percentage, they may believe that the answer is always in percent. For example; find 60% of £480. Children may be capable of calculating the answer of 288 but instead of writing down £288, they may write down 288%. Teachers will need to explain this issue and address to children that once calculating the answer, it must be in the same units as the given quantity.Hansen also comments that the key to succession in the understanding of percentages is the relationship and understanding the children have with fractions and decimals. For example: they should be aware that 50% is equivalent to ½ and 0.5, and 25% is equivalent to ¼ and 0.25. Teaching these topics in isolation of each other should be strictly avoided as this may destroy a child’s deep mathematical understanding. Killen and Hindhaugh agree with this as they noted that children need to continually link decimals, fractions and percentages to their knowledge of the number system and operations that they are familiar with. Reys, et al (2010) believes however that percentages are more closely linked with ratios and proportions in mathematics and how important it is for teachers to teach these other topics to a high level. This is to later reduce the amount of errors a child has over percentages. However, these theorists also agree that understanding percentages requires no more new skills or concepts beyond those used in identifying fractions, decimals, ratios and proportions. Reys, et al states that an effective way of starting these topics is to explore children’s basic knowledge of what percentage means to them.Barmby et al noted that a misconception occurs whenever a learner’s outlook of a task does not connect to the accepted meaning of the overall concept. Ryan and Williams state that it is more damaging for children to have misconceptions of mathematical concepts than difficulties calculating them. Killen and Hindhaugh begin to talk how the use of rules and recipes are commonly used more so by teachers that are not fully confident with percentages. The main point of the argument is that if children are taught these rules linked to percentages, misconceptions can occur. This could be caused if the child forgets or misapplies the rule to their working out.This method is not the most reliable for children but can be a quick alternative for teachers to teach their class, if they are not fully confident in the topic themselves. This links to one of the most common misconceptions in the primary classroom. Killen and Hindhaugh state that it is the teacher’s responsibility for their children’s successes in that subject area. If the teaching is effective, then the child will become more confident and develop more links revolving around the topic of percentages. This will result in the child having a high level of understanding. However, if the teaching is not up to standard the child may lose confidence in themselves and end up being confused with the simplest of questions.Q. Which one of the following is not a valid inference from the passage?

Direction: Read the following passage and answer the question that follows:There are several key difficulties surrounding the topic of percentages. Research has shown that there has been one difficulty which is more common than others; the meaning of the terms ‘of’ and ‘out of’. Hansen (2011) states that both terms represent an operator which needs explaining. Teachers need to address these before the topic is introduced to stop any confusion. ‘Of’ represents the multiplication operator, for example: 60% of 70 means 0.6 multiplied by 70; ‘out of’ represents the division operator, for example 30 out of 50 means 30 divided by 50. The teaching of these terms needs to be clear prior to teaching, so that children are confident in what these terms represent.Killen and Hindhaugh (2018) believe that once children understand that 1/10 is equal to 10% they will be able to use their knowledge of fractions to determine other multiples of 10. For example; Find 40% of 200. If children are aware that 10% is 20, then it will become obvious to them that 40% must be 80. This method enlightens many other practical ways to find other percentages of a quantity. Once children know 10%, they may also start finding half percent’s, such as; 5% or 25%. However, Killen and Hindhaugh (2018) state that a difficulty could occur when they are asking for a percentage of a quantity. If children are being asked to find the percentage, they may believe that the answer is always in percent. For example; find 60% of £480. Children may be capable of calculating the answer of 288 but instead of writing down £288, they may write down 288%. Teachers will need to explain this issue and address to children that once calculating the answer, it must be in the same units as the given quantity.Hansen also comments that the key to succession in the understanding of percentages is the relationship and understanding the children have with fractions and decimals. For example: they should be aware that 50% is equivalent to ½ and 0.5, and 25% is equivalent to ¼ and 0.25. Teaching these topics in isolation of each other should be strictly avoided as this may destroy a child’s deep mathematical understanding. Killen and Hindhaugh agree with this as they noted that children need to continually link decimals, fractions and percentages to their knowledge of the number system and operations that they are familiar with. Reys, et al (2010) believes however that percentages are more closely linked with ratios and proportions in mathematics and how important it is for teachers to teach these other topics to a high level. This is to later reduce the amount of errors a child has over percentages. However, these theorists also agree that understanding percentages requires no more new skills or concepts beyond those used in identifying fractions, decimals, ratios and proportions. Reys, et al states that an effective way of starting these topics is to explore children’s basic knowledge of what percentage means to them.Barmby et al noted that a misconception occurs whenever a learner’s outlook of a task does not connect to the accepted meaning of the overall concept. Ryan and Williams state that it is more damaging for children to have misconceptions of mathematical concepts than difficulties calculating them. Killen and Hindhaugh begin to talk how the use of rules and recipes are commonly used more so by teachers that are not fully confident with percentages. The main point of the argument is that if children are taught these rules linked to percentages, misconceptions can occur. This could be caused if the child forgets or misapplies the rule to their working out.This method is not the most reliable for children but can be a quick alternative for teachers to teach their class, if they are not fully confident in the topic themselves. This links to one of the most common misconceptions in the primary classroom. Killen and Hindhaugh state that it is the teacher’s responsibility for their children’s successes in that subject area. If the teaching is effective, then the child will become more confident and develop more links revolving around the topic of percentages. This will result in the child having a high level of understanding. However, if the teaching is not up to standard the child may lose confidence in themselves and end up being confused with the simplest of questions.Q. On the basis of the information in the passage, all of the following are potential problems children might face when learning percentages EXCEPT that they

Top Courses for CATView all

Top Courses for CAT

Radheshyam is an alcohol bootlegger. He wants to make an extra profit on the alcohol, hence he tried to dilute the alcohol. He does this in a unique way. He takes 625 Liters of alcohol in a tank that has a large capacity. He replaces 20% of the content with water. After this, he doubles the quantity of alcohol in the tank by adding pure alcohol and then doubles the percentage of water in the mixture by adding pure water.His manager found this process tiresome and confusing. Therefore he suggested Radheshyamto mix the original 625L alcohol with a solution B of alcohol and water so that the resulting solution is the same as that derived from his initial process. What is the overall quantity and concentration of the suggested mixture B?a)675.81L with 63.63% alcoholb)675.81L with 71.42% alcoholc)660.71L with 56.75% alcohold)785.71L with 71.42% alcoholCorrect answer is option 'C'. Can you explain this answer?
Question Description
Radheshyam is an alcohol bootlegger. He wants to make an extra profit on the alcohol, hence he tried to dilute the alcohol. He does this in a unique way. He takes 625 Liters of alcohol in a tank that has a large capacity. He replaces 20% of the content with water. After this, he doubles the quantity of alcohol in the tank by adding pure alcohol and then doubles the percentage of water in the mixture by adding pure water.His manager found this process tiresome and confusing. Therefore he suggested Radheshyamto mix the original 625L alcohol with a solution B of alcohol and water so that the resulting solution is the same as that derived from his initial process. What is the overall quantity and concentration of the suggested mixture B?a)675.81L with 63.63% alcoholb)675.81L with 71.42% alcoholc)660.71L with 56.75% alcohold)785.71L with 71.42% alcoholCorrect answer is option 'C'. Can you explain this answer? for CAT 2024 is part of CAT preparation. The Question and answers have been prepared according to the CAT exam syllabus. Information about Radheshyam is an alcohol bootlegger. He wants to make an extra profit on the alcohol, hence he tried to dilute the alcohol. He does this in a unique way. He takes 625 Liters of alcohol in a tank that has a large capacity. He replaces 20% of the content with water. After this, he doubles the quantity of alcohol in the tank by adding pure alcohol and then doubles the percentage of water in the mixture by adding pure water.His manager found this process tiresome and confusing. Therefore he suggested Radheshyamto mix the original 625L alcohol with a solution B of alcohol and water so that the resulting solution is the same as that derived from his initial process. What is the overall quantity and concentration of the suggested mixture B?a)675.81L with 63.63% alcoholb)675.81L with 71.42% alcoholc)660.71L with 56.75% alcohold)785.71L with 71.42% alcoholCorrect answer is option 'C'. Can you explain this answer? covers all topics & solutions for CAT 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for Radheshyam is an alcohol bootlegger. He wants to make an extra profit on the alcohol, hence he tried to dilute the alcohol. He does this in a unique way. He takes 625 Liters of alcohol in a tank that has a large capacity. He replaces 20% of the content with water. After this, he doubles the quantity of alcohol in the tank by adding pure alcohol and then doubles the percentage of water in the mixture by adding pure water.His manager found this process tiresome and confusing. Therefore he suggested Radheshyamto mix the original 625L alcohol with a solution B of alcohol and water so that the resulting solution is the same as that derived from his initial process. What is the overall quantity and concentration of the suggested mixture B?a)675.81L with 63.63% alcoholb)675.81L with 71.42% alcoholc)660.71L with 56.75% alcohold)785.71L with 71.42% alcoholCorrect answer is option 'C'. Can you explain this answer?.
Solutions for Radheshyam is an alcohol bootlegger. He wants to make an extra profit on the alcohol, hence he tried to dilute the alcohol. He does this in a unique way. He takes 625 Liters of alcohol in a tank that has a large capacity. He replaces 20% of the content with water. After this, he doubles the quantity of alcohol in the tank by adding pure alcohol and then doubles the percentage of water in the mixture by adding pure water.His manager found this process tiresome and confusing. Therefore he suggested Radheshyamto mix the original 625L alcohol with a solution B of alcohol and water so that the resulting solution is the same as that derived from his initial process. What is the overall quantity and concentration of the suggested mixture B?a)675.81L with 63.63% alcoholb)675.81L with 71.42% alcoholc)660.71L with 56.75% alcohold)785.71L with 71.42% alcoholCorrect answer is option 'C'. Can you explain this answer? in English & in Hindi are available as part of our courses for CAT. Download more important topics, notes, lectures and mock test series for CAT Exam by signing up for free.
Here you can find the meaning of Radheshyam is an alcohol bootlegger. He wants to make an extra profit on the alcohol, hence he tried to dilute the alcohol. He does this in a unique way. He takes 625 Liters of alcohol in a tank that has a large capacity. He replaces 20% of the content with water. After this, he doubles the quantity of alcohol in the tank by adding pure alcohol and then doubles the percentage of water in the mixture by adding pure water.His manager found this process tiresome and confusing. Therefore he suggested Radheshyamto mix the original 625L alcohol with a solution B of alcohol and water so that the resulting solution is the same as that derived from his initial process. What is the overall quantity and concentration of the suggested mixture B?a)675.81L with 63.63% alcoholb)675.81L with 71.42% alcoholc)660.71L with 56.75% alcohold)785.71L with 71.42% alcoholCorrect answer is option 'C'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of Radheshyam is an alcohol bootlegger. He wants to make an extra profit on the alcohol, hence he tried to dilute the alcohol. He does this in a unique way. He takes 625 Liters of alcohol in a tank that has a large capacity. He replaces 20% of the content with water. After this, he doubles the quantity of alcohol in the tank by adding pure alcohol and then doubles the percentage of water in the mixture by adding pure water.His manager found this process tiresome and confusing. Therefore he suggested Radheshyamto mix the original 625L alcohol with a solution B of alcohol and water so that the resulting solution is the same as that derived from his initial process. What is the overall quantity and concentration of the suggested mixture B?a)675.81L with 63.63% alcoholb)675.81L with 71.42% alcoholc)660.71L with 56.75% alcohold)785.71L with 71.42% alcoholCorrect answer is option 'C'. Can you explain this answer?, a detailed solution for Radheshyam is an alcohol bootlegger. He wants to make an extra profit on the alcohol, hence he tried to dilute the alcohol. He does this in a unique way. He takes 625 Liters of alcohol in a tank that has a large capacity. He replaces 20% of the content with water. After this, he doubles the quantity of alcohol in the tank by adding pure alcohol and then doubles the percentage of water in the mixture by adding pure water.His manager found this process tiresome and confusing. Therefore he suggested Radheshyamto mix the original 625L alcohol with a solution B of alcohol and water so that the resulting solution is the same as that derived from his initial process. What is the overall quantity and concentration of the suggested mixture B?a)675.81L with 63.63% alcoholb)675.81L with 71.42% alcoholc)660.71L with 56.75% alcohold)785.71L with 71.42% alcoholCorrect answer is option 'C'. Can you explain this answer? has been provided alongside types of Radheshyam is an alcohol bootlegger. He wants to make an extra profit on the alcohol, hence he tried to dilute the alcohol. He does this in a unique way. He takes 625 Liters of alcohol in a tank that has a large capacity. He replaces 20% of the content with water. After this, he doubles the quantity of alcohol in the tank by adding pure alcohol and then doubles the percentage of water in the mixture by adding pure water.His manager found this process tiresome and confusing. Therefore he suggested Radheshyamto mix the original 625L alcohol with a solution B of alcohol and water so that the resulting solution is the same as that derived from his initial process. What is the overall quantity and concentration of the suggested mixture B?a)675.81L with 63.63% alcoholb)675.81L with 71.42% alcoholc)660.71L with 56.75% alcohold)785.71L with 71.42% alcoholCorrect answer is option 'C'. Can you explain this answer? theory, EduRev gives you an ample number of questions to practice Radheshyam is an alcohol bootlegger. He wants to make an extra profit on the alcohol, hence he tried to dilute the alcohol. He does this in a unique way. He takes 625 Liters of alcohol in a tank that has a large capacity. He replaces 20% of the content with water. After this, he doubles the quantity of alcohol in the tank by adding pure alcohol and then doubles the percentage of water in the mixture by adding pure water.His manager found this process tiresome and confusing. Therefore he suggested Radheshyamto mix the original 625L alcohol with a solution B of alcohol and water so that the resulting solution is the same as that derived from his initial process. What is the overall quantity and concentration of the suggested mixture B?a)675.81L with 63.63% alcoholb)675.81L with 71.42% alcoholc)660.71L with 56.75% alcohold)785.71L with 71.42% alcoholCorrect answer is option 'C'. Can you explain this answer? tests, examples and also practice CAT tests.
Explore Courses for CAT exam

Top Courses for CAT

Explore Courses

Suggested Free Tests

Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.
10M+ students study on EduRev
Get App
© EduRev
Education Revolution
Follow Us
Signup to see your scores go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup